Kapitel

Definition der bedingten Wahrscheinlichkeit
Wir werden uns ansehen, wie sich die Wahrscheinlichkeit eines Ereignisses  verändert, wenn bekannt ist, dass ein anderes Ereignis
verändert, wenn bekannt ist, dass ein anderes Ereignis  eingetreten ist.
eingetreten ist.
Diese Wahrscheinlichkeit wird als bedingte Wahrscheinlichkeit des Ereignisses  bezeichnet, da das Ereignis
bezeichnet, da das Ereignis  eingetreten ist.
eingetreten ist.
Die Notation für diese bedingte Wahrscheinlichkeit lautet  . Der Einfachheit halber wird diese Notation einfach als bedingte Wahrscheinlichkeit von
. Der Einfachheit halber wird diese Notation einfach als bedingte Wahrscheinlichkeit von  unter der Bedingung
unter der Bedingung  gelesen.
gelesen.
Also sind  und
und  zwei beliebige Ereignisse desselben Stichprobenraums
zwei beliebige Ereignisse desselben Stichprobenraums  , sodass
, sodass 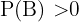 gilt, also:
gilt, also:
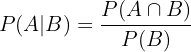
Beispiel für die Berechnung der bedingten Wahrscheinlichkeit
Berechne die Wahrscheinlichkeit, beim Würfeln eine  zu erzielen, wenn du weißt, dass eine gerade Zahl gewürfelt wurde.
zu erzielen, wenn du weißt, dass eine gerade Zahl gewürfelt wurde.
Lösung:
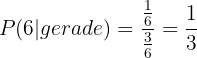
Bedingte Wahrscheinlichkeit für unabhängige Ereignisse
Zwei Ereignisse,  und
und  , sind unabhängig voneinander, wenn die Wahrscheinlichkeit, dass
, sind unabhängig voneinander, wenn die Wahrscheinlichkeit, dass  eintritt, nicht davon beeinflusst wird, ob
eintritt, nicht davon beeinflusst wird, ob  eingetreten ist oder nicht.
eingetreten ist oder nicht.
Wenn wir beispielsweise zweimal eine Münze werfen, wird das zweite Ergebnis nicht vom ersten Ergebnis beeinflusst.
Wenn zwei Ereignisse  und
und  unabhängig sind, ist
unabhängig sind, ist 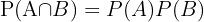 .
.
Wenn also 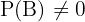 , ergibt sich aus der Definition der bedingten Wahrscheinlichkeit:
, ergibt sich aus der Definition der bedingten Wahrscheinlichkeit:
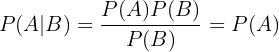
Mit anderen Worten: Wenn zwei Ereignisse  und
und  unabhängig voneinander sind, dann ist die bedingte Wahrscheinlichkeit von
unabhängig voneinander sind, dann ist die bedingte Wahrscheinlichkeit von  , wenn bekannt ist, dass
, wenn bekannt ist, dass  eingetreten ist, gleich der unbedingten Wahrscheinlichkeit von
eingetreten ist, gleich der unbedingten Wahrscheinlichkeit von  , wenn keine Informationen über
, wenn keine Informationen über  vorliegen. Das umgekehrte Ergebnis gilt ebenfalls, wenn:
vorliegen. Das umgekehrte Ergebnis gilt ebenfalls, wenn:
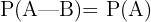
somit müssen die Ereignisse  und
und  unabhängig sein.
unabhängig sein.
Abhängige Ereignisse
Zwei Ereignisse,  und
und  , sind voneinander abhängig, wenn die Wahrscheinlichkeit, dass
, sind voneinander abhängig, wenn die Wahrscheinlichkeit, dass  eintritt, davon beeinflusst wird, ob
eintritt, davon beeinflusst wird, ob  eingetreten ist oder nicht.
eingetreten ist oder nicht.
Zwei Ereignisse  und
und  sind abhängig, wenn:
sind abhängig, wenn:
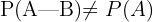
Mit KI zusammenfassen:












