Das Gaußsche Eliminiationsverfahren oder Gauß-Verfahren ist eine Technik in der linearen Algebra, mit der lineare Gleichungssysteme gelöst und die Stufenform oder reduzierte Zeilenstufenform einer Matrix ermittelt werden kann, was die Berechnungen vereinfacht.
In dieser Reihe von Übungen werden wir verschiedene Probleme mit dem Gaußschen Eliminationsverfahren untersuchen und dir die Möglichkeit geben, deine Fähigkeiten in dieser wichtigen mathematischen Methode zu entwickeln. Los geht's!
System mit 3 Gleichungen und 2 Variablen
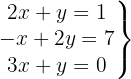
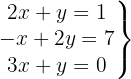
Wir schreiben das System als Matrix

Wir wenden das Gauß-Verfahren an



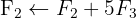

Das Gleichungssystem ist eindeutig lösbar
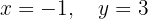
System mit 3 Gleichungen und 2 Variablen
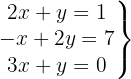
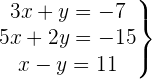
Wir schreiben das System als Matrix
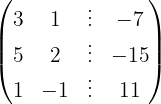
Wir wenden das Gauß-Verfahren an

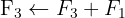

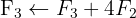

Das Gleichungssystem ist eindeutig lösbar
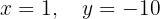
System mit 2 Gleichungen und 3 Variablen
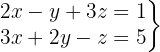
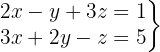
Wir schreiben das System als Matrix
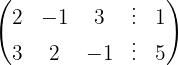
Wir wenden das Gauß-Verfahren an


Das Gleichungssystem ist unlösbar
Wir parametrisieren die Lösung mit  . Somit lautet die 2. Gleichung:
. Somit lautet die 2. Gleichung:

Das heißt 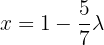 .
.
Die 1. Gleichung lautet 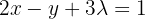 . Wenn wir
. Wenn wir  bestimmen, erhalten wir:
bestimmen, erhalten wir:
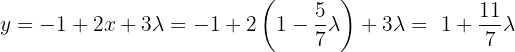
Das heißt 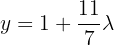 .
.
System mit 2 Gleichungen und 3 Variablen
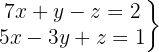
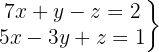
Wir schreiben das System als Matrix
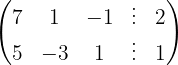
Wir wenden das Gauß-Verfahren an


Das Gleichungssystem ist unlösbar
Wir parametrisieren die Lösung mit  . Somit lautet die 2. Gleichung:
. Somit lautet die 2. Gleichung:
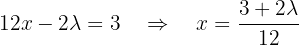
Das heißt  .
.
Die 1. Gleichung lautet  . Wenn wir
. Wenn wir  bestimmten, erhalten wir:
bestimmten, erhalten wir:
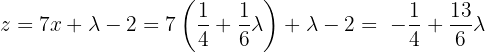
Das heißt 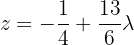 .
.
System mit 3 Gleichungen und 3 Variablen mit ähnlichen Koeffizienten
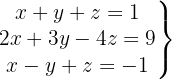
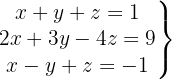
Wir schreiben das System als Matrix

Wir wenden das Gauß-Verfahren an


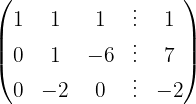
Das Gleichungssystem ist eindeutig lösbar
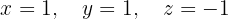
System mit 2 Gleichungen und 3 Variablen
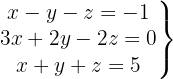
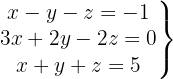
Wir schreiben das System als Matrix

Wir wenden das Gauß-Verfahren an
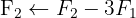

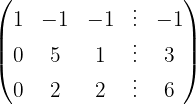

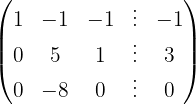
Das Gleichungssystem ist eindeutig lösbar
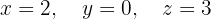
System mit 3 Gleichungen und 3 Variablen
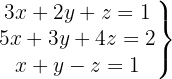
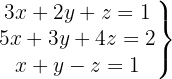
Wir schreiben das System als Matrix
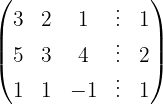
Wir wenden das Gauß-Verfahren an
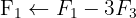
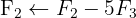

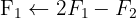
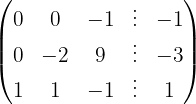
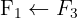
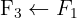
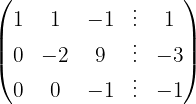
Das System ist eindeutig lösbar

System mit 3 Gleichungen und 3 Variablen
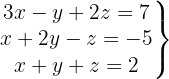
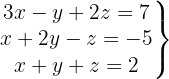
Wir schreiben das System als Matrix
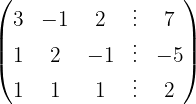
Wir wenden das Gauß-Verfahren an
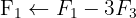
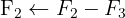

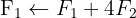

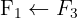
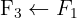

Das Gleichungssystem ist eindeutig lösbar

Überprüfe, ob folgendes Gleichungssystem eindeutig lösbar oder unlösbar ist
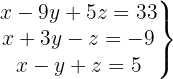
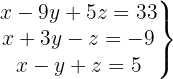
Wir schreiben das System als Matrix

Wir wenden das Gauß-Verfahren an
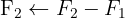


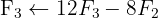

Das Gleichungssystem ist unlösbar

Überprüfe, ob folgendes Gleichungssystem eindeutig lösbar oder unlösbar ist
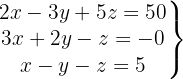
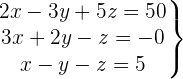
Wir schreiben das System als Matrix

Wir wenden das Gauß-Verfahren an

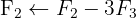

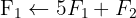

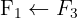
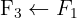

Das Gleichungssystem ist eindeutig lösbar

System mit 4 Gleichungen und 4 Variablen
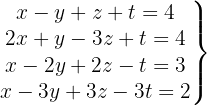
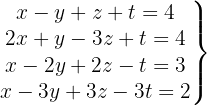
Wir schreiben das System als Matrix

Wir wenden das Gauß-Verfahren an


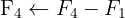
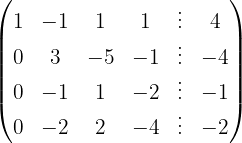
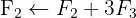


Das System ist unlösbar
Das Gleichungssystem ist unterbestimmt, da die letzte Zeile weggefallen ist. Wir parametrisieren die Lösung mit  . Die 2. Gleichung lautet:
. Die 2. Gleichung lautet:
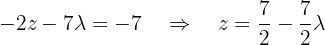
Ab hier können wir  in Bezug auf
in Bezug auf  audrücken, indem wir die 3. Gleichung nutzen. Diese lautet:
audrücken, indem wir die 3. Gleichung nutzen. Diese lautet:
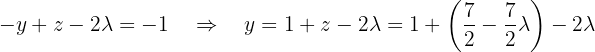

Als Letztes nutzen wir die 1. Gleichung, um  in Bezug auf
in Bezug auf  auszudrücken:
auszudrücken:
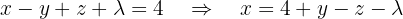
Das heißt:
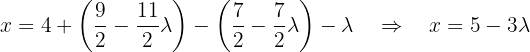
System mit 4 Gleichungen und 4 Variablen
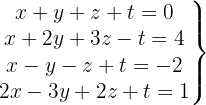
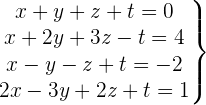
Wir schreiben das System als Matrix

Wir wenden das Gauß-Verfahren an
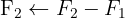

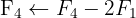

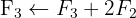


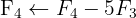

Das Gleichungssystem ist eindeutig lösbar

Überprüfe die Unlösbarkeit des Systems mit 4 Gleichungen
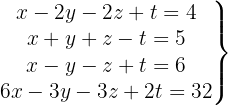
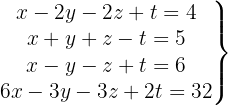
Wir schreiben das System als Matrix

Wir wenden das Gauß-Verfahren an
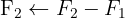

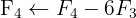




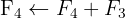

Das Gleichungssystem ist unlösbar
Wir stellen fest, dass das System unterbestimmt ist, da die letzte Zeile weggefallen ist. Wir parametrisieren die Lösung mit 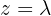 . Die 2. Gleichung lautet:
. Die 2. Gleichung lautet:
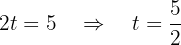
Ab hier können wir  in Bezug auf
in Bezug auf  ausdrücken, indem wir die 3. Gleichung nutzen. Diese lautet:
ausdrücken, indem wir die 3. Gleichung nutzen. Diese lautet:

Als Letztes nutzen wir die 1. Gleichung, um  in Bezug auf
in Bezug auf  auszudrücken:
auszudrücken:

Somit
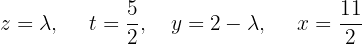
Überprüfe die Unlösbarkeit des Systems mit 4 Gleichungen
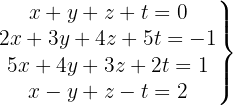
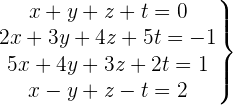
Wir schreiben das System als Matrix
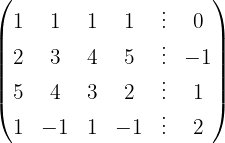
Wir wenden das Gauß-Verfahren an

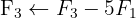

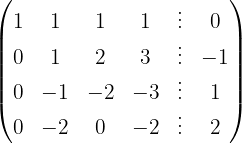


Das Gleichungssystem ist unlösbar
Das System ist unterbestimmt, da die 3. Zeile weggefallen ist. Wir parametrisieren die Lösung mit  . Die 2. Gleichung lautet:
. Die 2. Gleichung lautet:
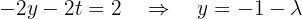
Ab hier können wir  in Bezug auf
in Bezug auf  ausdrücken, indem wir die 3. Gleichung nutzen. Diese lautet:
ausdrücken, indem wir die 3. Gleichung nutzen. Diese lautet:

Als Letztes nutzen wir die 1. Gleichung, um  in Bezug auf
in Bezug auf  auszudrücken:
auszudrücken:
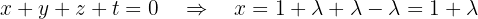
Somit
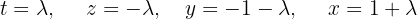
Löse das Gleichungssystem mit 3 Gleichungen und 5 Variablen
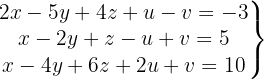
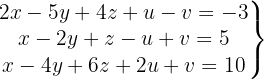
Wir schreiben das System als Matrix
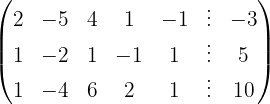
Wir wenden das Gauß-Verfahren an
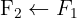
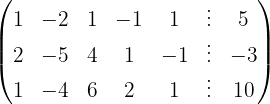


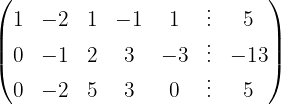

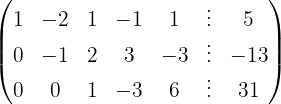
Das Gleichungssystem ist unlösbar
Wir parametrisieren die Lösung mit  . Die 3. Gleichung lautet:
. Die 3. Gleichung lautet:
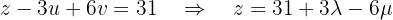
Ab hier können wir  in Bezug auf
in Bezug auf 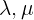 ausdrücken, indem wir die 2. Gleichung nutzen. Diese lautet:
ausdrücken, indem wir die 2. Gleichung nutzen. Diese lautet:
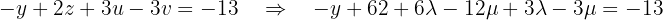
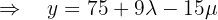
Als Letztes nutzen wir die 1. Gleichung, um  in Bezug auf
in Bezug auf 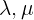 auszudrücken:
auszudrücken:


Somit
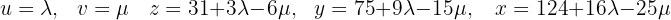
Löse das Gleichungssystem mit 3 Gleichungen und 5 Variablen
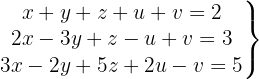
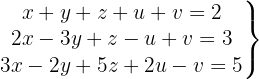
Wir schreiben das System als Matrix
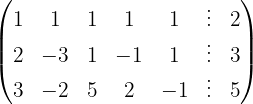
Wir wenden das Gauß-Verfahren an


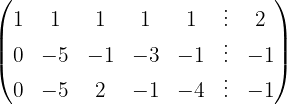
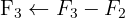
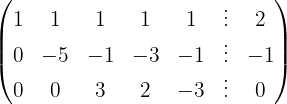
Das Gleichungssystem ist unlösbar
Wir parametrisieren die Lösung mit  . Die 3. Gleichung lautet:
. Die 3. Gleichung lautet:
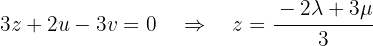
Ab hier können wir  in Bezug auf
in Bezug auf 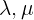 ausdrücken, indem wir die 2. Gleichung nutzen. Diese lautet:
ausdrücken, indem wir die 2. Gleichung nutzen. Diese lautet:


Als Letztes nutzen wir die 1. Gleichung, um  in Bezug auf
in Bezug auf 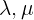 auszudrücken:
auszudrücken:

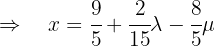
Somit
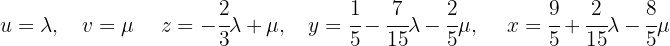
Löse das System mit 4 Gleichungen und 3 Variablen
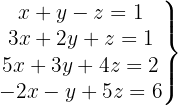
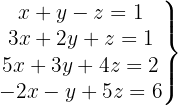
Wir schreiben das System als Matrix

Wir wenden das Gauß-Verfahren an
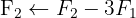
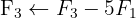
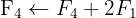


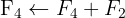
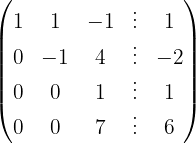

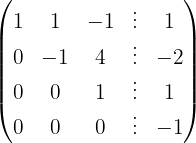
Das Gleichungssystem ist unlösbar
Löse das System mit 4 Gleichungen und 3 Variablen
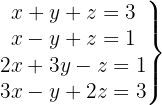
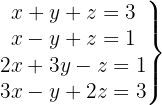
Wir schreiben das System als Matrix
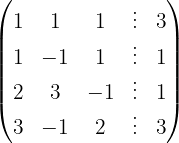
Wir wenden das Gauß-Verfahren an
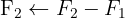
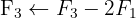
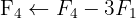
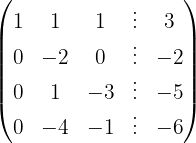



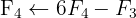

Das Gleichungssystem ist eindeutig lösbar
Mit KI zusammenfassen:



