Kapitel

Gesetz der totalen Wahrscheinlichkeit
Wir nehmen an, dass zwei Ereignisse 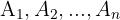 eine Partition auf den Ergebnisraum
eine Partition auf den Ergebnisraum  bilden. Das heißt, die Ereignisse
bilden. Das heißt, die Ereignisse 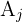 sind paarweise unvereinbar und bilden zusammen den Ergebnissraum
sind paarweise unvereinbar und bilden zusammen den Ergebnissraum  . Somit gilt
. Somit gilt 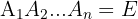 . Außerdem:
. Außerdem: 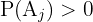 für
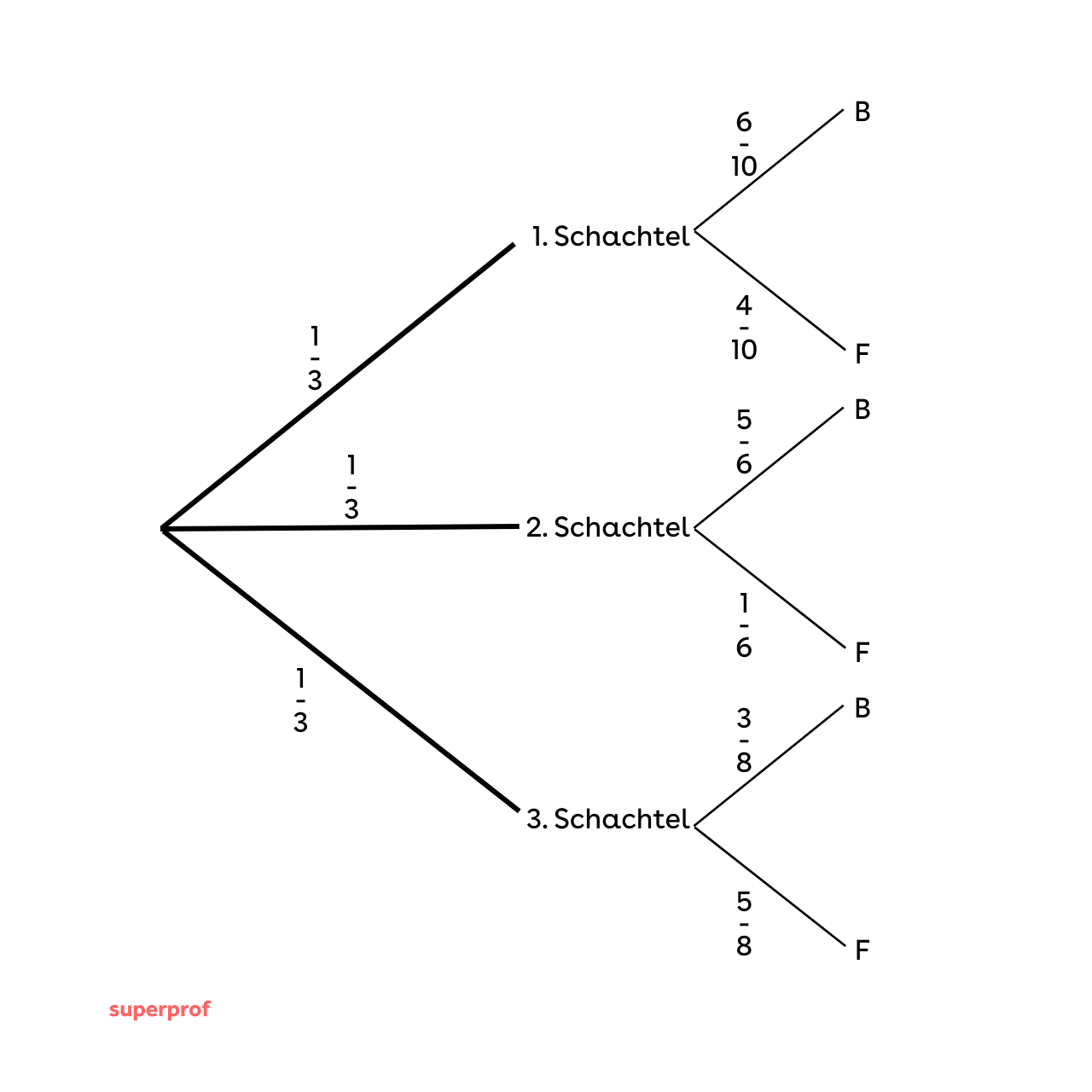
für 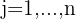 . Also gilt für ein beliebiges Ereignis
. Also gilt für ein beliebiges Ereignis  von
von  :
:

Beispiel für das Gesetz der totalen Wahrscheinlichkeit
1Es gibt drei Schachteln mit Glühbirnen. Die erste enthält  Glühbirnen, von denen vier durchgebrannt sind; in der zweiten sind sechs Glühbirnen, von denen eine durchgebrannt ist, und in der dritten Schachtel sind drei von insgesamt acht Glühbirnen durchgebrannt. Wie hoch ist die Wahrscheinlichkeit, dass eine zufällig aus einer der Schachteln entnommene Glühbirne durchgebrannt ist?
Glühbirnen, von denen vier durchgebrannt sind; in der zweiten sind sechs Glühbirnen, von denen eine durchgebrannt ist, und in der dritten Schachtel sind drei von insgesamt acht Glühbirnen durchgebrannt. Wie hoch ist die Wahrscheinlichkeit, dass eine zufällig aus einer der Schachteln entnommene Glühbirne durchgebrannt ist?
Lösung:
Wir notieren folgende Ereignisse:
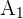 : Glühbirne aus Schachtel
: Glühbirne aus Schachtel  nehmen.
nehmen.
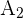 : Glühbirne aus Schachtel
: Glühbirne aus Schachtel  nehmen.
nehmen.
 : Glühbirne aus Schachtel
: Glühbirne aus Schachtel  nehmen.
nehmen.
 : Defekte Glühbirnen.
: Defekte Glühbirnen.
Unter Berücksichtigung des Gesetzes des totalen Wahrscheinlichkeit gilt:

Die Wahrscheinlichkeit, eine Glühbirne aus einer beliebigen Schachtel zu nehmen, beträgt  , und die Wahrscheinlichkeit, eine durchgebrannte Glühbirne aus jeder der Schachteln zu ziehen, hängt von der Gesamtzahl der Glühbirnen in der Schachtel und der Anzahl der durchgebrannten Glühbirnen in derselben Schachtel ab.
, und die Wahrscheinlichkeit, eine durchgebrannte Glühbirne aus jeder der Schachteln zu ziehen, hängt von der Gesamtzahl der Glühbirnen in der Schachtel und der Anzahl der durchgebrannten Glühbirnen in derselben Schachtel ab.
Die Wahrscheinlichkeit, eine durchgebrannte Glühbirne zu ziehen, ist die Summe der Wahrscheinlichkeiten, eine durchgebrannte Glühbirne aus jeder Schachtel zu ziehen, und kann wie folgt berechnet werden:
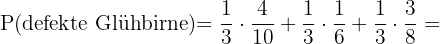
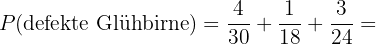
Um die Brüche zu addieren, ermitteln wir den kleinsten gemeinsamen Nenner und multiplizieren jeden Bruch mit der entsprechenden Zahl.
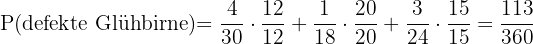
Mit KI zusammenfassen:












