Ein Barbesitzer hat alkoholfreie Getränke, Bier und Wein für 500 € (ohne Steuern) gekauft. Der Wert des Weins liegt um 60 € unter dem Wert der Erfrischungsgetränke und des Biers zusammen. Da auf alkoholfreie Getränke 6 %, auf Bier 12 % und auf Wein 30 % Mehrwertsteuer anfallen, beträgt die Gesamtrechnung mit Steuern 592,40 €. Berechne den Betrag, der für die einzelnen Getränke ausgegeben wurde.
Wir definieren die zu verwendenden Variablen: 
= Betrag in € für Erfrischungsgetränke.
= Betrag in € für Bier.
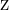= Betrag in € für Wein.
Wir erhalten folgendes Gleichungssystem:
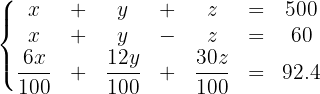
Wir vereinfachen die 3. Gleichung und erhalten:
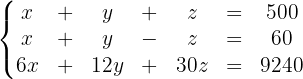
Um das System zu lösen, wenden wir die Cramersche Regel an:
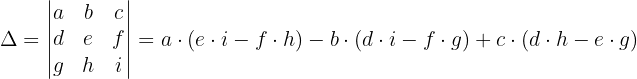
Wir wenden dieses Verfahren auf unser Gleichungssystem an und erhalten:
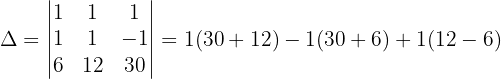
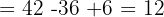
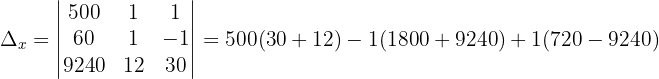
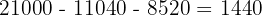
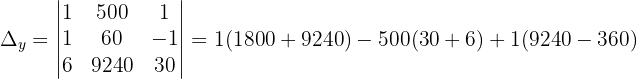
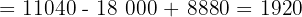
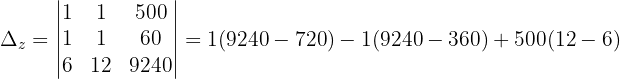
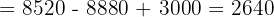
Schließlich berechnen wir die Werte der Variablen:
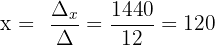
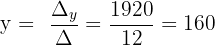
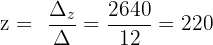
Die Lösungen sind:
x = 120 €
y = 160 €
z = 220 €
Ein Unternehmen besitzt drei Minen mit Erzen unterschiedlicher Zusammensetzung:
| Nickel (%) | Kupfer (%) | Eisen (%) | |
|---|---|---|---|
| Mine A | 1 | 2 | 3 |
| Mine B | 2 | 5 | 7 |
| Mine C | 1 | 3 | 1 |
Wie viele Tonnen von jeder Mine müssen verwendet werden, um 7 Tonnen Nickel, 18 Tonnen Kupfer und 16 Tonnen Eisen zu gewinnen?
Wir definieren die zu verwendenden Variablen:
= Anzahl Tonnen Mine A.
= Anzahl Tonnen Mine B.
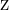= Anzahl Tonnen Mine C.
Wir erhalten folgendes Gleichungssystem:
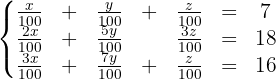
Wir vereinfachen und erhalten:
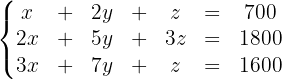
Um das System zu lösen, wenden wir die Cramersche Regel an:
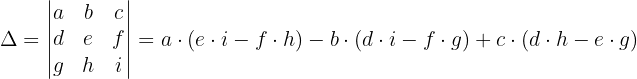
Wir wenden dieses Verfahren auf unser Gleichungssystem an und erhalten:
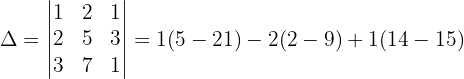
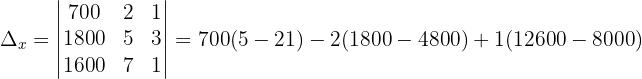
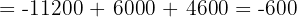
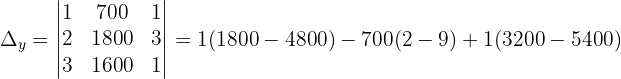
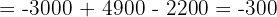
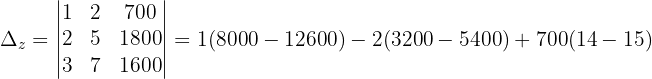
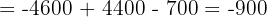
Schließlich berechnen wir die Werte der Variablen:
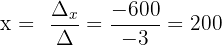
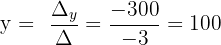
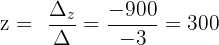
Die Lösungen sind:
x = 200 t
y = 100 t
z = 300 t
Das Alter eines Vaters ist das Doppelte der Summe des Alters seiner beiden Söhne, während das Alter des Vaters vor einigen Jahren (genau die Differenz des derzeitigen Alters der Söhne) das Dreifache der Summe des damaligen Alters seiner Söhne war. Wenn so viele Jahre vergangen sind wie die Summe der jetzigen Alter der Kinder, beträgt die Summe des Alters der drei Personen 150 Jahre. Wie alt war der Vater zur Zeit der Geburt seiner Kinder?
Wir definieren die zu verwendenden Variablen: = Aktuelles Alter des Vaters.
= Aktuelles Alter des älteren Sohnes.
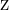= Aktuelles Alter des jüngeren Sohnes.
Aktuelle Relation: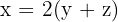 
Vor y − z Jahren: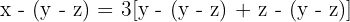 
Zwischen y + z: 
Somit haben wir das folgende Gleichungssystem: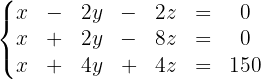
Um das System zu lösen, wenden wir die Cramersche Regel an:
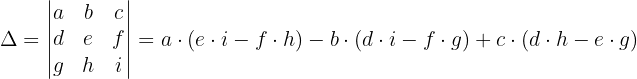
Wir wenden dieses Verfahren auf unser Gleichungssystem an und erhalten:
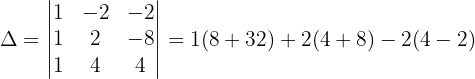
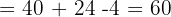
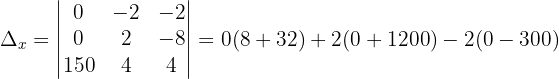
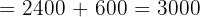
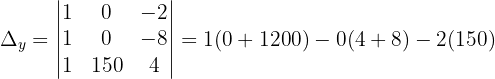
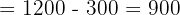
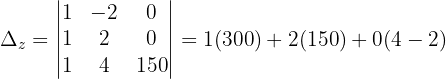
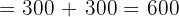
Schließlich berechnen wir die Werte der Variablen: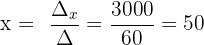
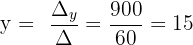
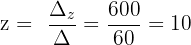
Somit:
Bei der Geburt seiner Kinder war der Vater 
und 
Jahre alt.
Drei Getreidesorten werden verkauft: Weizen, Gerste und Hirse.
Jede Menge Weizen wird für 4 € verkauft, Gerste für 2 € und Hirse für 0,5 €.
Wenn insgesamt eine Menge von 100 verkauft wird und 100 € für den Verkauf erhalten werden, welche Menge wird dann von jeder Getreidesorte verkauft?
Wir definieren die zu verwendenden Variablen: = Menge an Weizen.
= Menge an Gerste.
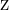= Menge an Hirse.
Wir erhalten folgendes Gleichungssystem:
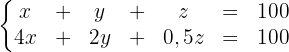
Wir multiplizieren die zweite Gleichung mit 2 und schreiben das System um:
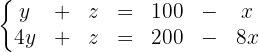
Um das System zu lösen, wenden wir die Cramersche Regel an:
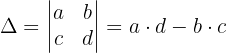
Wir wenden dieses Verfahren auf unser Gleichungssystem an und erhalten:
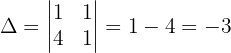
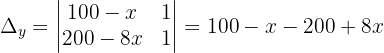
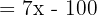
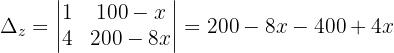
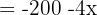
Zwei der Variablen hängen von der Variable x ab
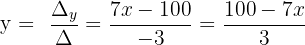
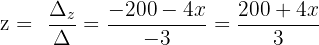
Wenn man davon ausgeht, dass die drei Variablen natürliche Zahlen sind und ihre Summe 100 ist, erhält man die folgenden Lösungen:
| S1 | S2 | S3 | S4 | S5 | |
|---|---|---|---|---|---|
| x | 1 | 4 | 7 | 10 | 13 |
| y | 31 | 24 | 17 | 10 | 3 |
| z | 68 | 72 | 76 | 80 | 84 |
Es gibt drei Edelmetallbarren, die wie folgt zusammengesetzt sind:
Der erste besteht aus 20 g Gold, 30 g Silber und 40 g Kupfer.
Der zweite besteht aus 30 g Gold, 40 g Silber und 50 g Kupfer.
Der dritte besteht aus 40 g Gold, 50 g Silber und 90 g Kupfer.
Welches Gewicht sollte von jedem der vorherigen Barren genommen werden, um einen neuen Barren mit 34 g Gold, 46 g Silber und 67 g Kupfer zu bilden?
= Gewicht des 1. Barrens.
= Gewicht des 2. Barrens.
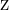= Gewicht des 3. Barrens.
Der Goldgehalt des 1. Barrens beträgt: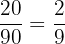
Der Goldgehalt des 2. Barrens beträgt: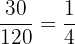
Der Goldgehalt des 3. Barrens beträgt: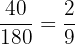
Die Gleichung für Gold lautet:
Der Silbergehalt des 1. Barrens beträgt: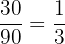
Der Silbergehalt des 2. Barrens beträgt: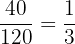
Der Silbergehalt des 3. Barrens beträgt: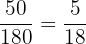
Die Gleichung für Silber lautet:
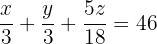
Der Kupfergehalt des 1. Barrens beträgt: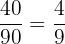
Der Kupfergehalt des 2. Barrens beträgt: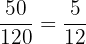
Der Kupfergehalt des 3. Barrens beträgt: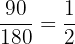
Die Gleichung für Kupfer lautet:
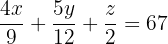
Mit den Gleichungen erhalten wir folgendes Gleichungssystem:
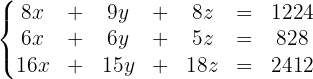
Um das System zu lösen, wenden wir die Cramersche Regel an:
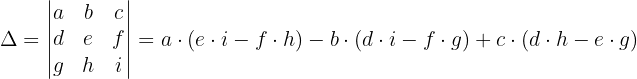
Wir wenden dieses Verfahren auf unser Gleichungssystem an und erhalten:
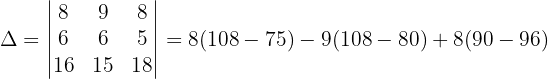
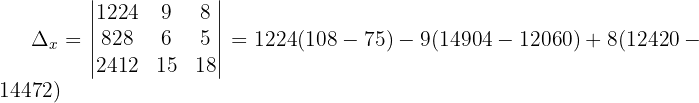
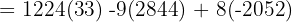
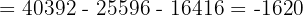
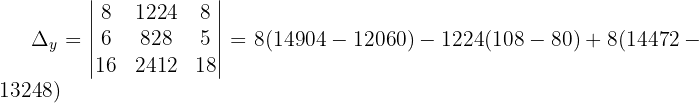
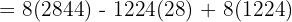
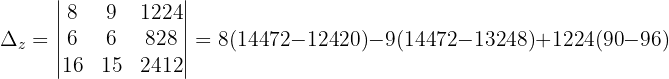
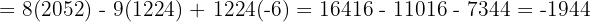
Schließlich berechnen wir die Werte der Variablen:
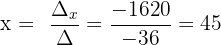
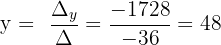
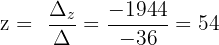
Die Lösung ist:
x = 45 y = 48 z = 54
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
