Untersuche und, wenn möglich, löse das System: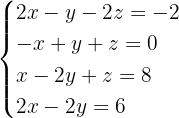
1 Wir bilden die Koeffizientenmatrix und berechnen ihren Rang.
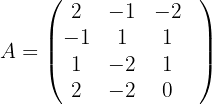
Ihr Rang ist größer als 1, somit
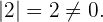
Ihr Rang ist größer als 2, weshalb
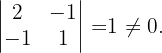
Ihr Rang ist größer als 3, weshalb
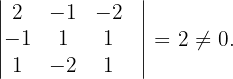
Es ist nicht möglich zu berechnen, ob sie einen Rang größer als 4 hat, da es sich nicht um eine Matrix der Dimension  handelt. Somit ist
handelt. Somit ist 
2 Wir bilden die erweiterte Matrix und berechnen ihren Rang.
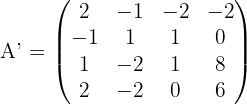
Da
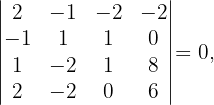
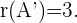
3 Wir wenden den Satz von Kronecker-Capelli an und sehen, da das System eindeutig lösbar ist. Somit
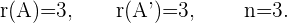
4Da das System eine eindeutige Lösung hat, können wir es entweder mit der Cramerschen Regel oder mit dem Gauß-Verfahren lösen. Da die vierte Zeile der Matrix  eine Linearkombination der anderen drei Zeilen ist, nehmen wir das Untersystem von
eine Linearkombination der anderen drei Zeilen ist, nehmen wir das Untersystem von  und seine entsprechende Matrix.
und seine entsprechende Matrix.
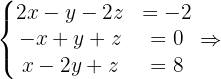
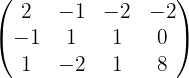
In diesem Fall lösen wir das System mit der Cramerschen Regel.
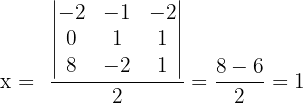
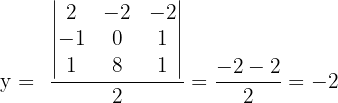
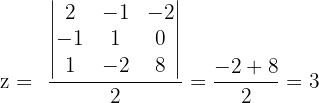
Für das ursprüngliche System erhalten wir 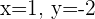 und
und 
Untersuche und, wenn möglich, löse das System: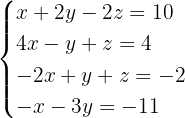
1 Wir bilden die Koeffizientenmatrix und berechnen ihren Rang.
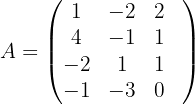
Ihr Rang ist größer als 1, weshalb

Ihr Rang ist größer als 2, weshalb
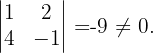
Ihr Rang ist größer als 3, weshalb
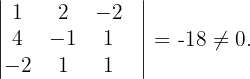
Es ist nicht möglich zu berechnen, ob sie einen Rang größer als 4 hat, da es sich nicht um eine Matrix der Dimension  handelt. Somit ist
handelt. Somit ist 
2 Wir bilden die erweiterte Matrix und berechnen ihren Rang.
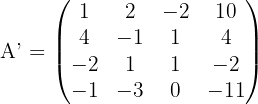
Da
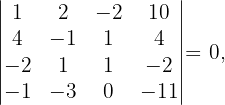
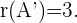
3 Wir wenden den Satz von Kronecker-Capelli an und sehen, dass das System eindeutig lösbar ist. Somit
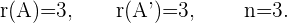
4 Da das System eine eindeutige Lösung hat, können wir es entweder mit der Cramerschen Regel oder mit dem Gauß-Verfahren lösen. Da die vierte Zeile der Matrix  eine Linearkombination der anderen drei Zeilen ist, nehmen wir das Untersystem von
eine Linearkombination der anderen drei Zeilen ist, nehmen wir das Untersystem von  und seine entsprechende Matrix.
und seine entsprechende Matrix.
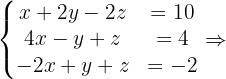
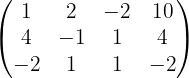
In diesem Fall lösen wir das System mit der Cramerschen Regel.
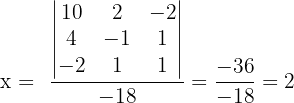
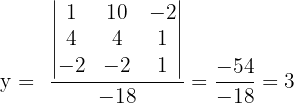
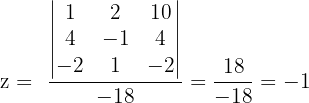
Somit erhalten wir für das ursprüngliche System 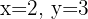 und
und 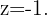
Untersuche und, wenn möglich, löse das System: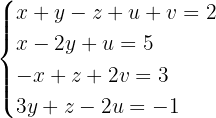
1 Wir bilden die Koeffizientenmatrix und berechnen ihren Rang.
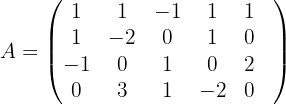
Ihr Rang ist größer als 1, weshalb

Ihr Rang ist größer als 2, weshalb
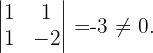
Ihr Rang ist größer als 3, weshalb
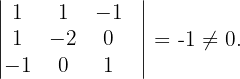

Es ist nicht möglich zu berechnen, ob sie einen Rang größer als 5 hat, da es sich nicht um eine Matrix der Dimension  handelt. Somit ist
handelt. Somit ist 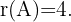
2 Wir bilden die erweiterte Matrix und berechnen ihren Rang.
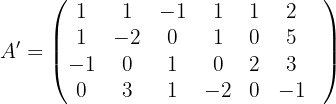
Da wir keine Untermatrix der Ordnung größer als  erhalten können, ist
erhalten können, ist
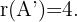
3 Wir wenden den Satz von Kronecker-Capelli an und sehen, dass das System nicht eindeutig lösbar ist. Somit

4 Das System hat keine eindeutige Lösung und wir können es mit der Cramerschen Regel lösen. Wir setzen  . Wir nehmen das Untersystem von
. Wir nehmen das Untersystem von  und seine entsprechende Matrix.
und seine entsprechende Matrix.
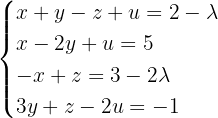
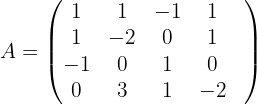
In diesem Fall lösen wir das System mit der Cramerschen Regel.
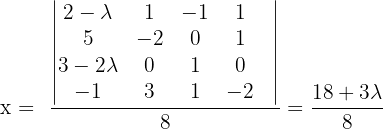
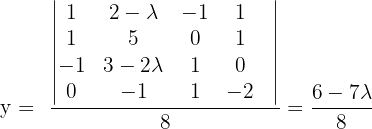
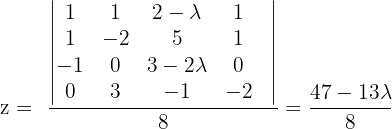
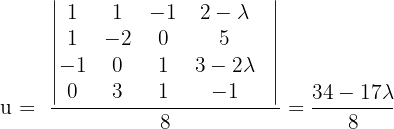
Untersuche und, wenn möglich, löse das System: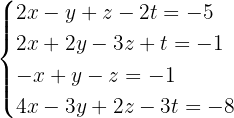
1 Wir bilden die Koeffizientenmatrix und berechnen ihren Rang.
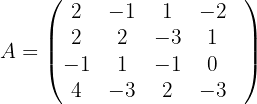
Ihr Rang ist größer als 1, weshalb
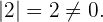
Ihr Rang ist größer als 2, weshalb
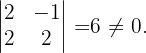
Ihr Rang ist größer als 3, weshalb
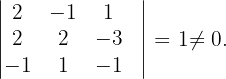
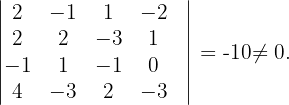
Es ist nicht möglich zu berechnen, ob sie einen Rang größer als 4 hat, da es sich nicht um eine Matrix der Dimension  handelt. Somit
handelt. Somit 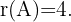
2 Wir bilden die erweiterte Matrix und berechnen ihren Rang.
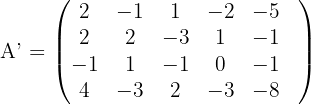
Da es keine Untermatrix der Ordnung größer als  gibt, ist
gibt, ist
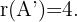
3 Wir wenden den Satz von Kronecker-Capelli an und sehen, dass das System eindeutig lösbar ist. Somit
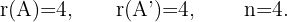
4 Das System ist eindeutig lösbar und wir können es mit der Cramerschn Regel oder dem Gauß-Verfahren lösen.
In diesem Fall lösen wir das System mit der Cramerschen Regel.



Schließlich können wir den Wert von  ermitteln, indem wir eine der Gleichungen des Systems auflösen, beispielsweise
ermitteln, indem wir eine der Gleichungen des Systems auflösen, beispielsweise 
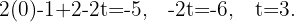
Untersuche und löse das System, wenn möglich.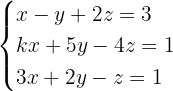
1 Wir bilden die Koeffizientenmatrix und berechnen ihren Rang.
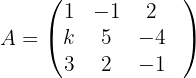
Ihr Rang ist größer als 1, weshalb

Ihr Rang ist größer als 2, weshalb
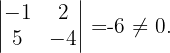
Da
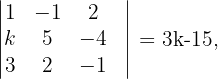
haben wir zwei Fälle für den Rang der Koeffizientenmatrix. Wenn  , ist der Rang
, ist der Rang 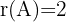 und wenn
und wenn 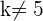 , ist der Rang
, ist der Rang  .
.
2 Wir bilden die erweiterte Matrix und berechnen ihren Rang.
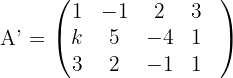
Da es eine Untermatrix der Ordnung  mit der Determinante ungleich 0 gibt:
mit der Determinante ungleich 0 gibt:
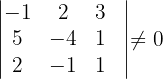 ,
,
ist 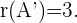
3 Wir wenden den Satz von Kronecker-Capelli an und sehen, dass das System eindeutig lösbar ist. Wenn also 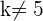 , ist
, ist  . Wenn
. Wenn  , ist
, ist  und das System nicht lösbar.
und das System nicht lösbar.
4 In diesem Fall lösen wir das System mit der Cramerschen Regel (oder mit dem Gauß-Verfahren).
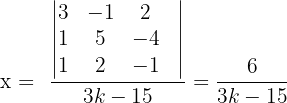
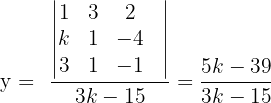
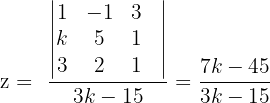
Untersuche und löse das System, wenn möglich.
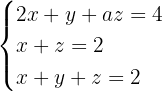
1 Wir bilden die Koeffizientenmatrix und berechnen ihren Rang.
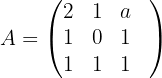
Ihr Rang ist größer als 1, weshalb

Ihr Rang ist größer als 2, weshalb
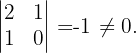
Da
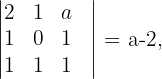
haben wir zwei Fälle für den Rang der Koeffizientenmatrix. Wenn 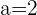 , ist der Rang
, ist der Rang 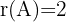 und wenn
und wenn 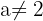 , ist der Rang
, ist der Rang  .
.
2 Wir bilden die erweiterte Matrix und berechnen ihren Rang.
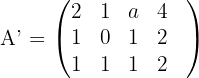
Da die vierte Spalte der Matrix  das Doppelte der ersten Spalte der Matrix
das Doppelte der ersten Spalte der Matrix  ist, können wir unsere Matrix
ist, können wir unsere Matrix  auf die Matrix
auf die Matrix  reduzieren. Das heißt,
reduzieren. Das heißt,
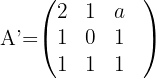
Somit ist 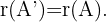
3 Wir wenden den Satz von Kronecker-Capelli an und sehen, dass das System eindeutig lösbar ist, wenn 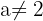 . Somit ist
. Somit ist 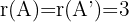 und
und 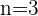 . Wenn
. Wenn 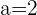 , ist
, ist  ,
, 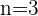 und das System nicht eindeutig lösbar.
und das System nicht eindeutig lösbar.
4 In diesem Fall lösen wir das System mit der Cramerschen Regel (oder dem Gauß-Verfahren).
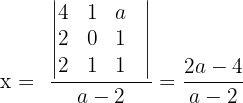
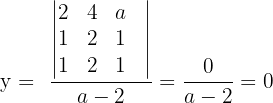
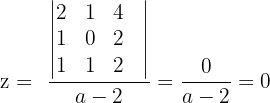
Wir können auch etwas über das nicht eindeutig lösbare System sagen. Wenn 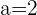 und
und  , ist
, ist 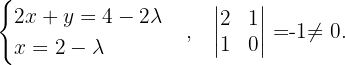 Und auch
Und auch 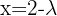 und
und 
Untersuche und löse das System, wenn möglich.
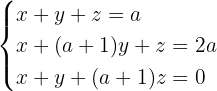
1 Wir bilden die Koeffizientenmatrix und berechnen ihren Rang.
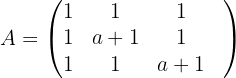
Ihr Rang ist größer als 1, weshalb

Die Determinante einer beliebigen Untermatrix der Ordnung  ist
ist 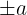 oder
oder 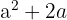
Da
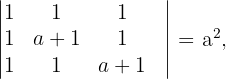
haben wir zwei Fälle für den Rang der Koeffizientenmatrix. Wenn 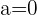 , ist der Rang
, ist der Rang  und wenn
und wenn 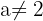 , ist der Rang
, ist der Rang  .
.
2 Wir bilden die erweiterte Matrix und berechnen ihren Rang.
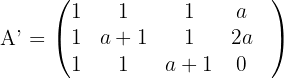
Wenn 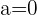 , ist
, ist
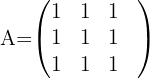
und
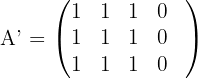
3 Wir wenden den Satz von Kronecker-Capelli an und sehen, dass das System eindeutig lösbar ist, wenn 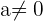 . Somit ist
. Somit ist 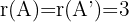 und
und 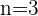 . Wenn
. Wenn 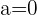 , ist
, ist 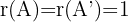 ,
, 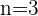 und das System also nicht eindeutig lösbar.
und das System also nicht eindeutig lösbar.
4 In diesem Fall lösen wir das System mit der Cramerschen Regel (oder dem Gauß-Verfahren).
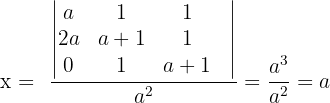
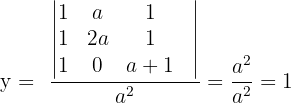
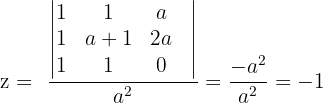
Wir können auch etwas über das nicht eindeutig lösbare System sagen. Wenn 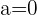 und
und 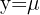 , ist
, ist  und somit
und somit  Schließlich ist
Schließlich ist 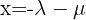 .
.
Untersuche und löse das System, wenn möglich.
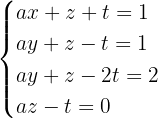
1 Wir bilden die Koeffizientenmatrix und berechnen ihren Rang.
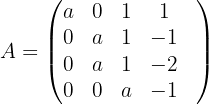
Die Determinante dieser Matrix ist

2 Wir bilden die erweiterte Matrix und berechnen ihren Rang.
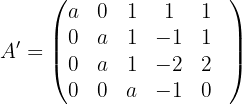
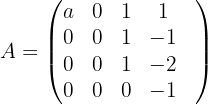
und
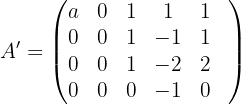
3 Wir wenden den Satz von Kronecker-Capelli an und sehen, dass das System eindeutig lösbar ist, wenn 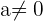 . Somit ist
. Somit ist 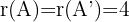 und
und  . Wenn
. Wenn 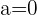 , ist
, ist 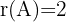 und
und 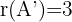 . Also gibt es Untermatrizen von
. Also gibt es Untermatrizen von  der Ordnung 2 und 3 mit einer Determinante ungleich 0. Somit ist das System nicht lösbar.
der Ordnung 2 und 3 mit einer Determinante ungleich 0. Somit ist das System nicht lösbar.
4 In diesem Fall lösen wir das System mit dem Gauß-Verfahren.
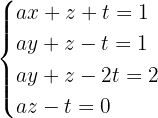
Wenn wir die 2. Zeile von der 3. Zeile subtrahieren, erhalten wir 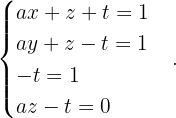
Also ist 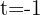 . Und schließlich
. Und schließlich 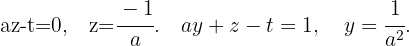
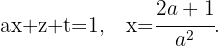
Untersuche das folgende System anhand der verschiedenen Werte von a und b.
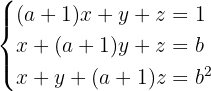
1 Wir bilden die Koeffizientenmatrix und die erweiterte Matrix. 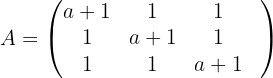
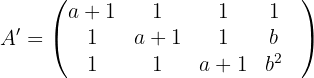 2 Wir berechnen die Determinante der Matrix
2 Wir berechnen die Determinante der Matrix 
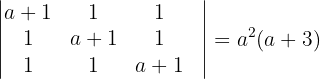 Wir stellen fest, dass die Matrix
Wir stellen fest, dass die Matrix  eine Untermatrix der Ordnung 2 hat und die Determinante gleich
eine Untermatrix der Ordnung 2 hat und die Determinante gleich 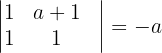 ist. Also haben wir verschiedene Fälle für die Berechnung des Rangs der Matrizen
ist. Also haben wir verschiedene Fälle für die Berechnung des Rangs der Matrizen  und
und  . Wir wenden den Satz von Kronecker-Capelli an. 3 Das System ist eindeutig lösbar, wenn
. Wir wenden den Satz von Kronecker-Capelli an. 3 Das System ist eindeutig lösbar, wenn 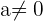 ,
, 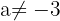 , und für alle
, und für alle  ist
ist 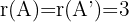 und
und 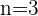 ; Dies ergibt sich aus der Tatsache, dass die Determinante von
; Dies ergibt sich aus der Tatsache, dass die Determinante von  ungleich 0 ist und dass
ungleich 0 ist und dass  keine Untermatrix der Ordnung größer als 3 hat. 4 Wenn
keine Untermatrix der Ordnung größer als 3 hat. 4 Wenn 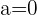 und
und  , ist
, ist 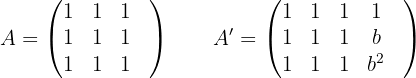 Daraus folgt
Daraus folgt  und aus
und aus  können wir die Determinante
können wir die Determinante 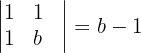 ableiten. Der Rang von
ableiten. Der Rang von  ist also 2. Daraus schließen wir, dass das System nicht lösbar ist. 5 Wenn
ist also 2. Daraus schließen wir, dass das System nicht lösbar ist. 5 Wenn  und
und 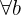 , ist
, ist 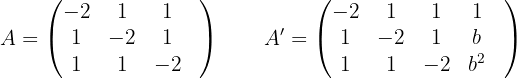 Daraus folgt
Daraus folgt 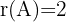 und aus
und aus  können wir die Determinante
können wir die Determinante 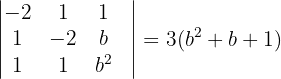 ableiten. Daraus schließen wir, dass der Rang von
ableiten. Daraus schließen wir, dass der Rang von  3 ist. Erneut ist das System nicht lösbar.
3 ist. Erneut ist das System nicht lösbar.
Untersuche und löse das System, wenn möglich.
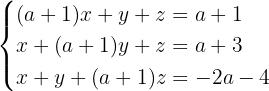
1 Wir bilden die Koeffizientenmatrix und die erweiterte Matrix.
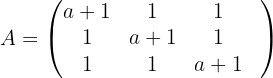
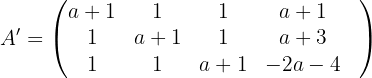
2 Wir berechnen die Determinante der Matrix 
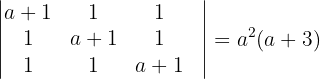
Wir stellen außerdem fest, dass die Matrix también que la matriz  eine Untermatrix der Ordnung 2 mit der folgenden Determinante hat
eine Untermatrix der Ordnung 2 mit der folgenden Determinante hat
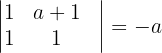
Auf diese Weise haben wir verschiedene Fälle, um den Rang der Matrizen  und
und  zu berechnen. Hierzu wenden wir den Satz von Kronecker-Capelli an.
zu berechnen. Hierzu wenden wir den Satz von Kronecker-Capelli an.
3 Das System ist eindeutig lösbar. Wenn 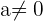 ,
, 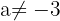 ist
ist 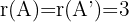 und
und 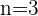 ; dies ergibt sich aus der Tatsache, dass die Determinante von
; dies ergibt sich aus der Tatsache, dass die Determinante von  ungleich 0 ist und dass
ungleich 0 ist und dass  keine Untermatrix der Ordnung größer als 3 hat. Wir lösen das System für diesen Fall mit der Cramerschen Regel.
keine Untermatrix der Ordnung größer als 3 hat. Wir lösen das System für diesen Fall mit der Cramerschen Regel.
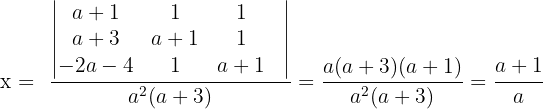
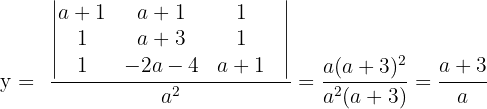
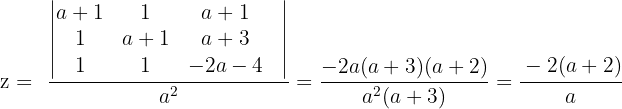
4 Wenn 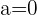 , ist
, ist
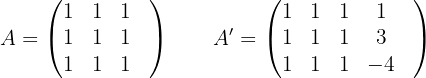
Daraus folgt, dass  und aus der
und aus der  können wir die folgende Determinante extrahieren
können wir die folgende Determinante extrahieren
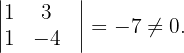
Somit ist der Rang von  gleich 2. Dies zeigt uns, dass das System nicht lösbar ist.
gleich 2. Dies zeigt uns, dass das System nicht lösbar ist.
5 Wenn  , ist
, ist
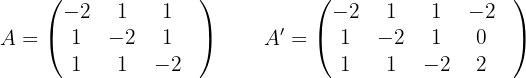
Daraus folgt, dass 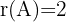 . Aus
. Aus  können wir die folgende Determinante extrahieren
können wir die folgende Determinante extrahieren
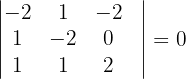
Der Rang von  ist 2. Das System ist nicht eindeutig lösbar. Wir wenden die Cramersche Regel an und mit
ist 2. Das System ist nicht eindeutig lösbar. Wir wenden die Cramersche Regel an und mit  können wir das Gleichungssystem für diesen Fall lösen,
können wir das Gleichungssystem für diesen Fall lösen, 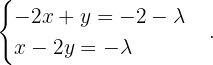 Da
Da
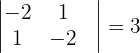 ,
,
haben wir
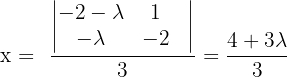
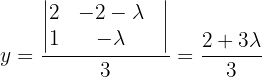
Untersuche und löse das System, wenn möglich.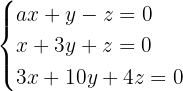
1 Wir bilden die Koeffizientenmatrix und berechnen ihren Rang.
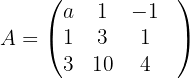
Die Determinante von  ist
ist
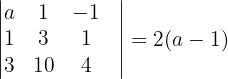
Für den Fall, dass  ist, ist der Rang von
ist, ist der Rang von  3 und
3 und 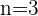 , was bedeutet, dass das System nur die triviale Lösung
, was bedeutet, dass das System nur die triviale Lösung 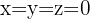 haben kann.
haben kann.
2 Wenn 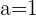 , ist der Rang der Matrix
, ist der Rang der Matrix  2 und somit
2 und somit
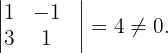 Da
Da 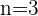 , ist das System nicht eindeutig lösbar und wir können es mit der Cramerschen Regel lösen. Wir nehmen
, ist das System nicht eindeutig lösbar und wir können es mit der Cramerschen Regel lösen. Wir nehmen  ,
,
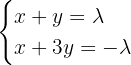
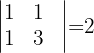
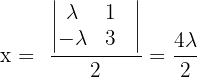
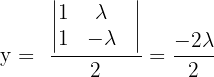
Untersuche das folgende System anhand der verschiedenen Werte von a und b.
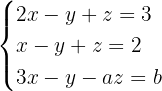
1 Wir bilden die Koeffizientenmatrix und die erweiterte Matrix.
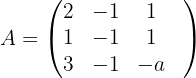
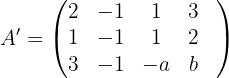
2 Wir berechnen die Determinante der Matrix 
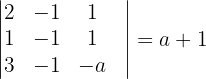
Wir stellen außerdem fest, dass die Matrix  eine Untermatrix der Ordnung 2 mit einer Determinante gleich 2 hat.
eine Untermatrix der Ordnung 2 mit einer Determinante gleich 2 hat.
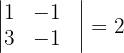
Auf diese Weise haben wir verschiedene Möglichkeiten, den Rang der Matrizen  und
und  zu berechnen. Hierzu wenden wir den Satz von Kronecker-Capelli an.
zu berechnen. Hierzu wenden wir den Satz von Kronecker-Capelli an.
3 Das System ist eindeutig lösbar, wenn  und somit ist
und somit ist 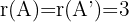 und
und 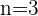 ; dies ergibt sich aus der Tatsache, dass die Determinante von
; dies ergibt sich aus der Tatsache, dass die Determinante von  ungleich 0 ist und dass
ungleich 0 ist und dass  keine Untermatrix der Ordnung größer als 3 mit einer Determinante von 0 hat.
keine Untermatrix der Ordnung größer als 3 mit einer Determinante von 0 hat.
4 Wenn 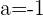 , ist
, ist
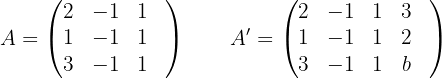
Daraus folgt, dass 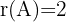 ist, und da aus
ist, und da aus  die folgende Determinante abgeleitet werden kann,
die folgende Determinante abgeleitet werden kann,
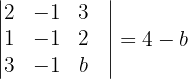
Wir schließen daraus, dass der Rang von  3 ist. Wenn
3 ist. Wenn  , ist das System nicht lösbar. Und wenn
, ist das System nicht lösbar. Und wenn  , können wir sagen, dass das System nicht eindeutig lösbar ist. Also ist
, können wir sagen, dass das System nicht eindeutig lösbar ist. Also ist  .
.
Mit KI zusammenfassen:


