Erörtere die folgenden Systeme und löse sie gegebenenfalls:
a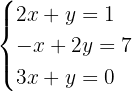 
b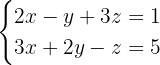 
span class="sa">aWir bilden zunächst die mit dem System verbundene erweiterte Koeffizientenmatrix
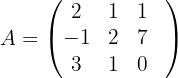
Wir skalieren die Matrix 
, indem wir die folgenden Operationen auf die Zeilen von anwenden. Wir benennen die Zeile 
von mit 
. 
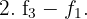
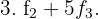Wir erhalten
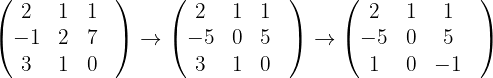
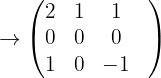
Die letzte Matrix zeigt uns Folgendes: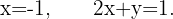 
Somit ist 
Da wir eine einzige Lösung haben, ist das System eindeutig lösbar.
bWir bilden zunächst die mit dem System verbundene erweiterte Koeffizientenmatrix
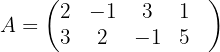
Wir skalieren die Matrix , indem wir die folgenden Operationen auf die Zeilen von anwenden. Wir benennen die Zeile von mit . 
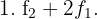Wir erhalten Folgendes
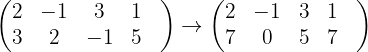
Wenn 
, für einen gegebenen Parameter 
; die letzte Matrix zeigt uns: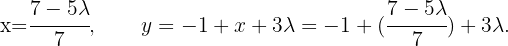 
Somit: 
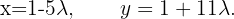Da wir unendlich viele Lösungen haben, ist das System nicht eindeutig lösbar.
Löse das folgende Gleichungssystem:
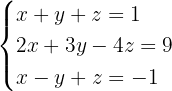
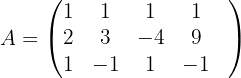
, indem wir die folgenden Operationen auf die Zeilen von anwenden. Wir benennen die Zeile von mit . 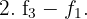Wir erhalten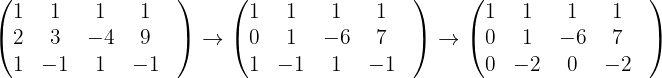 
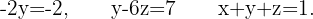Somit: 
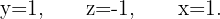Da wir eine einzige Lösung haben, ist das System eindeutig lösbar.Wir sehen uns folgendes System an: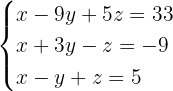 
aLöse es und klassifiziere es anhand der Anzahl der Lösungen.
bBestimme, ob es möglich ist, eine der Gleichungen zu eliminieren, so dass das resultierende System äquivalent zum vorherigen ist.
Wir bilden zunächst die mit dem System verbundene erweiterte Koeffizientenmatrix
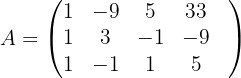
Wir skalieren die Matrix , indem wir die folgenden Operationen auf die Zeilen von anwenden. Wir benennen die Zeile von mit . 
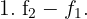
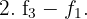
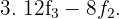Wir erhalten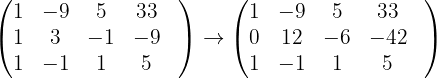 
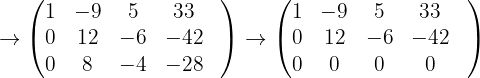
Wenn , für einen gegebenen Parameter ; die letzte Matrix zeigt uns: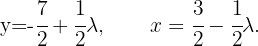 
Da wir unendlich viele Lösungen haben, ist das System nicht eindeutig lösbar. Wir können die 
Gleichung eliminieren, da sie eine lineare Kombination der anderen beiden Gleichungen ist. Das heißt, wir haben das folgende System:
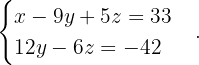
Klassifiziere und löse das System
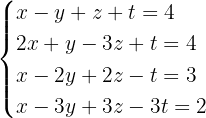
Wir bilden zunächst die mit dem System verbundene erweiterte Koeffizientenmatrix
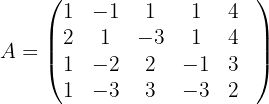
Wir skalieren die Matrix , indem wir die folgenden Operationen auf die Zeilen von anwenden. Wir benennen die Zeile von mit . 
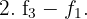
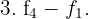
Wir erhalten
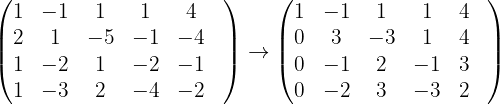
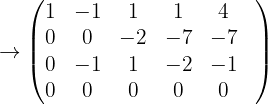
Wenn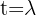 
, für einen gegebenen Parameter ; die letzte Matrix zeigt uns: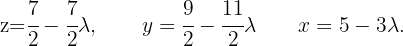 
Da wir unendlich viele Lösungen haben, ist das System nicht eindeutig lösbar.
Erörtere das System anhand der Werte des Parameters a.
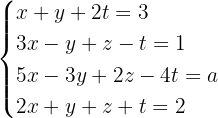
Wir bilden zunächst die mit dem System verbundene erweiterte Koeffizientenmatrix
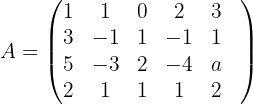
Wir skalieren die Matrix , indem wir die folgenden Operationen auf die Zeilen von anwenden. Wir benennen die Zeile von mit . 
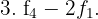
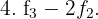
Wir erhalten
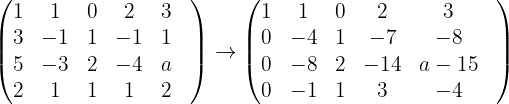
Aus der dritten Zeile der letzten Matrix ergibt sich Folgendes: 
Wir erhalten also ein nicht eindeutig lösbares System: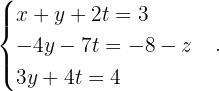 
Wenn 
, ist das System nicht lösbar ist, hätten wir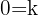 
für eine Konstante
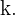
Untersuche das System auf seine Lösbarkeit anhand der Werte der Parameter a und b.
Falls möglich, löse es.
Wir bilden zunächst die mit dem System verbundene erweiterte Koeffizientenmatrix
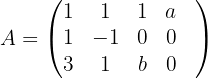
Wir skalieren die Matrix , indem wir die folgenden Operationen auf die Zeilen von anwenden. Wir benennen die Zeile von mit . 
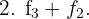
Wir erhalten
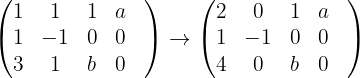
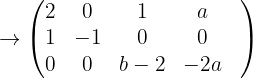
Wenn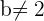 
, ist das System eindeutig lösbar und somit 
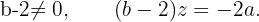Daraus folgen die folgenden Lösungen: 
Wenn 
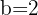und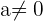 
, ist das System nicht lösbar und wir würden 
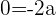erhalten. Wenn 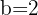und 
, ist das System eindeutig lösar und wir würden für einen Parameter das folgende System erhalten: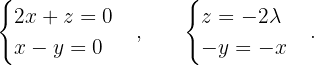 
Und somit
Bestimme, für welche Werte von k das folgende System unendlich viele Lösungen hat.
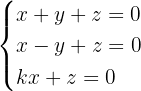
Wir bilden zunächst die mit dem System verbundene erweiterte Koeffizientenmatrix
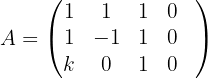
Wir skalieren die Matrix , indem wir die folgenden Operationen auf die Zeilen von anwenden. Wir benennen die Zeile von mit . 
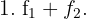
Wir erhalten
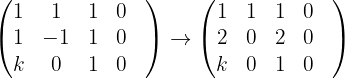
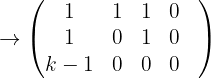
Da wir unendlich viele Lösungen suchen, ist 
Dies besagt, dass das System nicht eindeutig lösbar ist. Wir haben das folgende System und Lösungen für einen Parameter
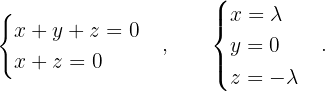
Ein Unternehmen besitzt drei Minen mit Erzen unterschiedlicher Zusammensetzung:
| Nickel (%) | Kupfer (%) | Eisen (%) | |
|---|---|---|---|
| Mine A | 1 | 2 | 3 |
| Mine B | 2 | 5 | 7 |
| Mine C | 1 | 3 | 1 |
Wie viele Tonnen von jeder Mine müssen verwendet werden, um 7 Tonnen Nickel, 18 Tonnen Kupfer und 16 Tonnen Eisen zu gewinnen?
Wir deklarieren die folgenden Variablen und stellen ein Gleichungssystem auf
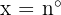Tonnen aus Mine A.
Tonnen aus Mine B.
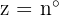Tonnen aus Mine C.
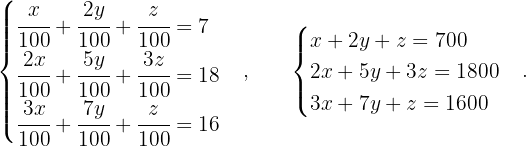Wir bilden zunächst die mit dem System verbundene erweiterte Koeffizientenmatrix
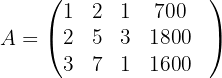
Wir skalieren die Matrix , indem wir die folgenden Operationen auf die Zeilen von anwenden. Wir benennen die Zeile von mit . 
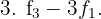Wir erhalten
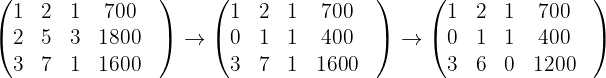
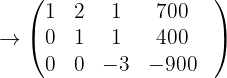
Die letzte Matrix gibt Folgendes an:
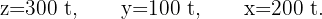
Das Alter eines Vaters ist das Doppelte der Summe des Alters seiner beiden Söhne, während das Alter des Vaters vor einigen Jahren (genau die Differenz des derzeitigen Alters der Söhne) das Dreifache der Summe des damaligen Alters seiner Söhne war. Wenn so viele Jahre vergangen sind wie die Summe der jetzigen Alter der Kinder, beträgt die Summe des Alters der drei Personen 150 Jahre. Wie alt war der Vater zur Zeit der Geburt seiner Kinder?
Wir geben die folgenden Variablen an und stellen ein Gleichungssystem entsprechend der in der Aufgabenstellung gegebenen Informationen auf
= Aktuelles Alter des Vaters.
= Aktuelles Alter des älteren Sohnes.
= Aktuelles Alter des jüngeren Sohnes.
Aktuelle Relation: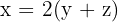 
Vor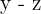 
Jahren: 
Zwischen y + z: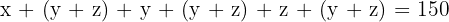 
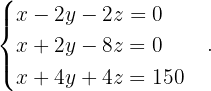Wir bilden zunächst die mit dem System verbundene erweiterte Koeffizientenmatrix
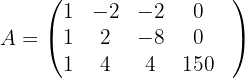
Wir skalieren die Matrix , indem wir die folgenden Operationen auf die Zeilen von anwenden. Wir benennen die Zeile von mit . 
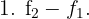
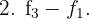
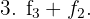Y obtenemos lo siguiente
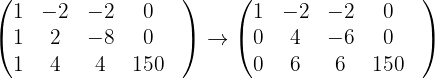
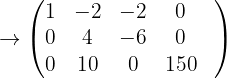
Die letzte Matrix gibt Folgendes an: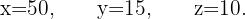 
Das System ist also eindeutig lösbar.
Der Vater war also bei der Geburt seiner Söhne jeweils 35 und 40 Jahre alt.
Drei Getreidesorten werden verkauft: Weizen, Gerste und Hirse.
Jede Menge Weizen wird für 4 € verkauft, Gerste für 2 € und Hirse für 0,5 €.
Wenn insgesamt eine Menge von 100 verkauft wird und 100 € für den Verkauf erhalten werden, welche Menge wird dann von jeder Getreidesorte verkauft?
Wir geben die folgenden Variablen an und stellen ein Gleichungssystem entsprechend der in der Aufgabenstellung gegebenen Informationen auf = Menge an Weizen.
= Menge an Gerste.
= Menge an Hirse.
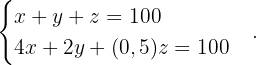
Da dieses System mehr Variablen als Gleichungen hat, ist es unterbestimmt. Wir erhalten folgende Information
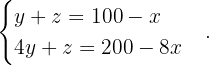
Wenn man davon ausgeht, dass die drei Variablen natürliche Zahlen sind und ihre Summe 100 ist, erhält man die folgenden Lösungen:
| S1 | S2 | S3 | S4 | S5 | |
|---|---|---|---|---|---|
| x | 1 | 4 | 7 | 10 | 13 |
| y | 31 | 24 | 17 | 10 | 3 |
| z | 68 | 72 | 76 | 80 | 84 |
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
