
Das Gleichsetzungsverfahren
Das Gleichsetzungsverfahren beruht auf dem Prinzip der Transitivität.
Wenn  und
und 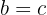 ,
,
weiß man dank der Transitivität, dass  .
.
Beispiel:
Wenn 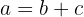 und
und  , ergibt sich
, ergibt sich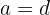 .
.
Dasselbe gilt für ein Gleichungssystem, bei dem dieses Verfahren angewendet wird.
Schritt 1: Wir wählen eine Variable aus, die in jeder Gleichung des Systems vorkommt.
Schritt 2: Wir bestimmen die Variable in jeder Gleichung.
Beispiel:
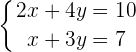
Wir können irgendeine der 2 Variablen bestimmen. In diesem Fall nehmen wir  . Wir denken daran, dass wir den Schritt in jeder der Gleichungen durchführen müssen.
. Wir denken daran, dass wir den Schritt in jeder der Gleichungen durchführen müssen.

Wir sehen, dass beide Gleichungen gleich  gesetzt werden. Aufgrund der Transitivität ergibt sich:
gesetzt werden. Aufgrund der Transitivität ergibt sich:
Wenn  und
und  , gilt
, gilt .
.
Nun bleibt uns noch eine Gleichung mit einer Variablen. Wir vereinfachen und erhalten:
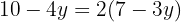
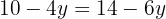

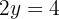

Wir setzen den Wert in irgendeine der 2 Gleichungen ein, um den Wert für  zu erhalten
zu erhalten
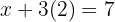
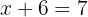


Übungsaufgaben zum Gleichsetzungsverfahren
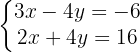
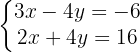 Wir bestimmen die Unbekannte x in der ersten und zweiten Gleichung
Wir bestimmen die Unbekannte x in der ersten und zweiten Gleichung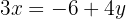

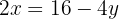
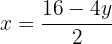
Wir setzen beide Ausdrücke gleich
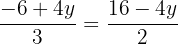
Wir lösen die Gleichung
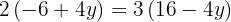
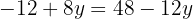
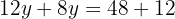


Wir setzen den Wert für  in einen der beiden Ausdrücke ein,
in einen der beiden Ausdrücke ein,
für den wir  bestimmt haben.
bestimmt haben.
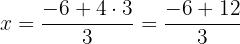

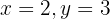
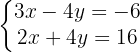 Wir bestimmen die Unbekannte x in der ersten und zweiten Gleichung
Wir bestimmen die Unbekannte x in der ersten und zweiten Gleichung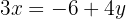

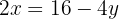
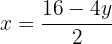
Wir setzen beide Ausdrücke gleich
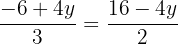
Wir lösen die Gleichung
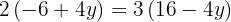
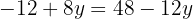
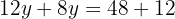


Wir setzen den Wert für  in einen der beiden Ausdrücke ein,
in einen der beiden Ausdrücke ein,
für den wir  bestimmt haben.
bestimmt haben.
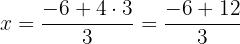

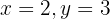
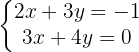 Wir bestimmen die Unbekannte
Wir bestimmen die Unbekannte  der ersten und zweiten Gleichung
der ersten und zweiten Gleichung

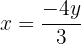
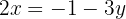
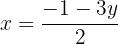
Wir setzen die Ausdrücke gleich

Wir lösen die Gleichung
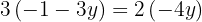
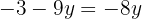

Wir setzen den Wert für y in einen der beiden Ausdrücke ein, für den wir  bestimmt haben
bestimmt haben

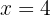
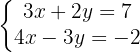
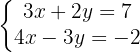
Wir bestimmen die Unbekannte  der ersten und zweiten
der ersten und zweiten
Gleichung.


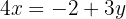

Wir setzen die Ausdrücke gleich und lösen die Gleichung.
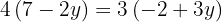
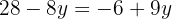

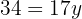

Wir setzen den Wert für y in einen der beiden Ausdrücke ein, für den wir bestimmt haben.
bestimmt haben.
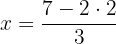

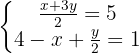
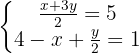
Um zu vereinfachen, multiplizieren wir die zweite Gleichung mit 2: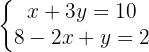
Wir ordnen die Terme
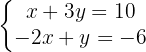
Wir bestimmen die Unbekannte x der ersten und zweiten Gleichung


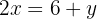
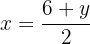
Wir setzen die Ausdrücke gleich und lösen die Gleichung.
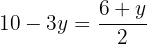

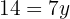

Wir setzen den Wert für  in einen der beiden Ausdrücke ein,
in einen der beiden Ausdrücke ein,
für den wir  bestimmt haben.
bestimmt haben.
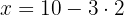
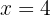
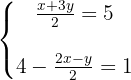
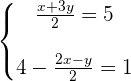 Wir formen um, sodass die Nenner wegfallen
Wir formen um, sodass die Nenner wegfallen
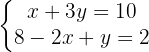
Wir ordnen die zweite Gleichung
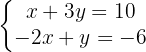
Wir bestimmen die Unbekannte x der ersten und zweiten Gleichung


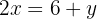
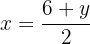
Wir setzen die Ausdrücke gleich
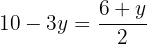
Wir lösen die Gleichung

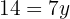

Wir setzen den Wert für  in einen der beiden Ausdrücke ein,
in einen der beiden Ausdrücke ein,
für den wir  bestimmt haben.
bestimmt haben.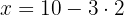
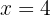
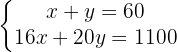
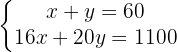 Wir bestimmen die Unbekannte x der ersten und zweiten Gleichung
Wir bestimmen die Unbekannte x der ersten und zweiten Gleichung

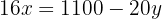
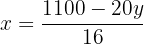
Wir setzen die Ausdrücke gleich
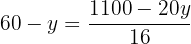
Wir lösen die Gleichung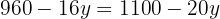
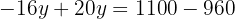

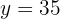
Wir setzen den Wert für  in einen der beiden
in einen der beiden
Ausdrücke ein, für den wir  bestimmt haben.
bestimmt haben.















