Kapitel

Entsprechend der Anzahl ihrer Lösungen
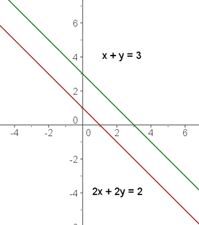
Eindeutig lösbares System
Ein System, das eine einzige Lösung hat.
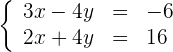
Graphisch dargestellt ist die Lösung der Schnittpunkt der zwei Geraden.
Mehrdeutig lösbares System
Ein System, das unendlich viele Lösungen hat.
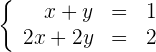
Graphisch dargestellt erhalten wir zwei aufeinanderliegende Geraden. Jeder Punkt auf der Geraden ist eine Lösung.
Unlösbares System
Ein System, das keine Lösung hat.

Graphisch dargestellt erhalten wir zwei parallele Geraden.
Äquivalente Gleichungssysteme
Äquivalente Gleichungssysteme haben dieselbe Lösung, obwohl die Anzahl der Gleichungen nicht übereinstimmt.
Wir erhalten äquivalente Gleichungssysteme durch Eliminierung der abhängigen Gleichungen, wenn:
1 Alle Koeffizienten sind null.
2 Zwei Zeilen sind gleich.
3 Eine Zeile ist proportional zu einer anderen Zeile.
4 Eine Zeile ist eine lineare Kombination aus anderen Zeilen.
Äquivalenzkriterien bei Gleichungssystemen
1 Wenn zu beiden Gliedern einer Gleichung eines Systems derselbe Ausdruck addiert oder von ihnen subtrahiert wird, ist das resultierende System äquivalent.
2 Wenn beide Glieder der Gleichungen eines Systems mit einer Zahl ungleich null multipliziert oder durch sie dividiert werden, ist das resultierende System äquivalent.
3 Wenn wir eine Gleichung eines Systems mit einer anderen Gleichung desselben Systems addieren oder von ihr subtrahieren, ist das resultierende System äquivalent zum gegebenen System.
4 Wenn eine Gleichung eines Systems durch eine andere Gleichung ersetzt wird, die sich aus der Addition der beiden Gleichungen des zuvor mit Zahlen ungleich null multiplizierten oder dividierten Systems ergibt, ist das Ergebnis ein anderes System, das äquivalent zum ersten System ist.
5 Wird die Reihenfolge der Gleichungen oder die Reihenfolge der Unbekannten in einem System geändert, so ergibt sich ein anderes äquivalentes System.
Gestaffelte Gleichungssyteme
Systeme, bei denen jede Gleichung eine Unbekannte weniger hat als die vorhergehende Gleichung.

Bei der dritten Gleichung ergibt sich  .
.
Wir setzen ihren Wert in die zweite Gleichung ein und erhalten somit  .
.
Wir setzen die vorherigen Werte in die erste Gleichung ein und erhalten 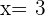 .
.
Auch hier handelt es sich um ein gestaffeltes System:
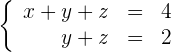
Da wir in diesem Fall mehr Unbekannte als Gleichungen haben, nehmen wir eine der Unbekannten (zum Beispiel  ) und hängen Sie an das zweite Glied.
) und hängen Sie an das zweite Glied.

Wir nehmen an, dass 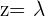 , wobei
, wobei  ein Parameter ist, der für irgendeinen reellen Wert steht.
ein Parameter ist, der für irgendeinen reellen Wert steht.
Somit sind die Lösungen:
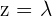
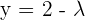
 .
.
Mit KI zusammenfassen:













