Kapitel
Wenn alle konstanten Glieder in einem System aus  Gleichungen und
Gleichungen und  Unbekannten null sind, ist das System homogen.
Unbekannten null sind, ist das System homogen.
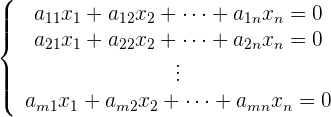
Für diese Arten von Systemen gibt es nur die triviale Lösung:  .
.
Der Ausdruck in Form einer Matrix ist gegeben durch
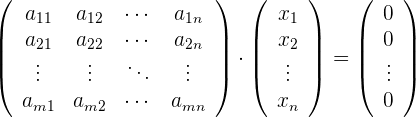
Wir stellen fest, dass jedes lineare homogene System lösbar ist, da es die triviale Lösung zulässt. Wie bestimmen wir aber, ob ein System bestimmt oder unbestimmt ist?
Die Antwort auf diese Frage wurde 1875 von dem französischen Mathematiker Eugène Rouché in seinem Artikel Sur la discussion des equations du premier degré gegeben. Dieser erschien in der 81. Ausgabe des Compte Rendus de la Académie des Sciences. Das Ergebnis, zu dem Rouché kam, ist im deutschen Sprachgebrauch als Satz von Kronecker-Capelli bekannt.

Satz von Kronecker-Capelli
Gegeben ist die Koeffizientenmatrix  und die erweiterte Matrix
und die erweiterte Matrix  des Systems aus
des Systems aus  linearen Gleichungen mit
linearen Gleichungen mit  Unbekannten. Wenn
Unbekannten. Wenn  und
und  der Rang von
der Rang von  und
und  sind, gilt:
sind, gilt:
Das System ist lösbar, wenn für die Ränge 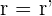 gilt. Außerdem, wenn gilt
gilt. Außerdem, wenn gilt 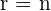 , ist das System eindeutig lösbar. Das heißt, es hat eine eindeutige Lösung.
, ist das System eindeutig lösbar. Das heißt, es hat eine eindeutige Lösung.
Ist das System lösbar und es gilt 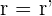 , aber
, aber 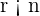 , ist das System mehrdeutig lösbar. Das heißt, es hat unendlich viele Lösungen.
, ist das System mehrdeutig lösbar. Das heißt, es hat unendlich viele Lösungen.
Das System ist unlösbar, wenn die Ränge unterschiedlich, also 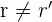 sind. Das System hat somit keine Lösung.
sind. Das System hat somit keine Lösung.
Satz von Kronecker-Capelli bei homogenen Systemen
Damit ein homogenes System andere Lösungen als die triviale Lösung hat, muss der Rang der Koeffizientenmatrix niedriger sein als die Anzahl der Unbekannten.
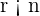
Für den Fall 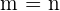 genügt es, dass die Determinante der Koeffizientenmatrix null ist.
genügt es, dass die Determinante der Koeffizientenmatrix null ist.
Das liegt daran, dass wir es hier mit dem Satz von Kronecker-Capelli zu tun haben. Hierbei gilt, 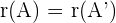 und der Wert ist niedriger als die Anzahl der Unbekannten. Somit ist das System mehrdeutig lösbar.
und der Wert ist niedriger als die Anzahl der Unbekannten. Somit ist das System mehrdeutig lösbar.
Beispiel: Bestimme, ob das System eindeutig oder mehrdeutig lösbar ist
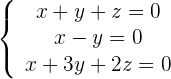
1 Wir bilden die Koeffizientenmatrix.
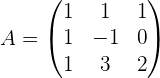
2 Wir berechnen den Rang der Koeffizientenmatrix.
Der Rang ist mindestens 1, da

Der Rang ist mindestens 2, da
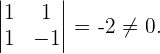
Rang 3 existiert nicht, da
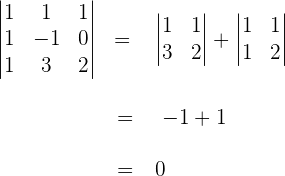
3 Da 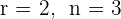 , stellen wir mit dem Satz von Kronecker-Capelli fest, dass das System mehrdeutig lösbar ist und unendlich viele Lösungen hat.
, stellen wir mit dem Satz von Kronecker-Capelli fest, dass das System mehrdeutig lösbar ist und unendlich viele Lösungen hat.
Beispiel: Bestimme, ob das folgende System eindeutig oder mehrdeutig lösbar ist
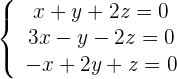
1 Wir bilden die Koeffizientenmatrix.
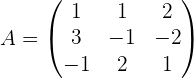
2 Da 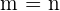 , berechnen wir anstatt des Rangs der Koeffizientenmatrix ihre Determinante
, berechnen wir anstatt des Rangs der Koeffizientenmatrix ihre Determinante
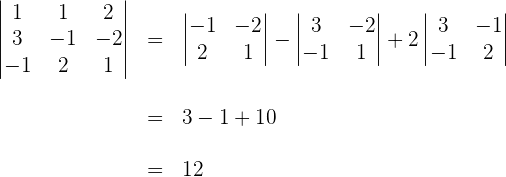
3 Da 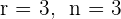 , stellen wir mit dem Satz von Kronecker-Capelli fest, dass das System eine eindeutige Lösung hat
, stellen wir mit dem Satz von Kronecker-Capelli fest, dass das System eine eindeutige Lösung hat
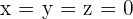
Übungsaufgaben zum Satz von Kronecker-Capelli
Bestimme, ob die folgenden homogenen Gleichungssysteme eindeutig oder mehrdeutig lösbar sind
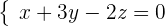
1 Wir bilden die Koeffizientenmatrix.
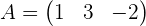
2 Der Rang der Koeffizientenmatrix ist 1, da

3 Da 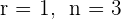 , stellen wir mit dem Satz von Kronecker-Capelli fest, dass das System mehrdeutig lösbar ist und unendlich viele Lösungen hat.
, stellen wir mit dem Satz von Kronecker-Capelli fest, dass das System mehrdeutig lösbar ist und unendlich viele Lösungen hat.
4 Wir berechnen die Lösungen, indem wir eine Variable durch die beiden anderen ausdrücken, da das System nur aus einer Gleichung besteht
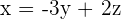
Wir setzen 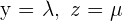 mit
mit 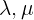 reellen Zahlen
reellen Zahlen
und erhalten die Lösungen der Form 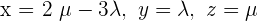
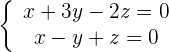
1 Wir bilden die Koeffizientenmatrix.
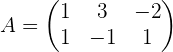
2 Der Rang der Koeffizientenmatrix ist 2, da
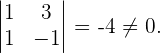
3 Da 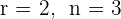 , stellen wir mit dem Satz von Kronecker-Capelli fest, dass das System mehrdeutig lösbar ist und unendlich viele Lösungen hat.
, stellen wir mit dem Satz von Kronecker-Capelli fest, dass das System mehrdeutig lösbar ist und unendlich viele Lösungen hat.
4 Wir berechnen die Lösungen. Hierzu wenden wir das Gaußsche Eliminationsverfahren an. Wir ersetzen die Zeile  durch
durch 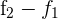
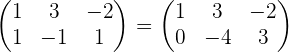
Wir erhalten ein äquivalentes System
Wir setzen 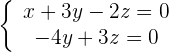
Wir setzen 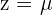 und erhalten
und erhalten
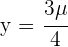 .
.
Wir ersetzen die Werte für 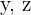 und erhalten
und erhalten
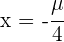 .
.
Die Lösungen haben die Form 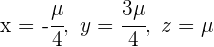
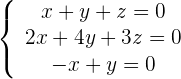
1 Wir bilden die Koeffizientenmatrix.
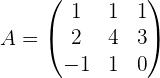
2 Wir berechnen die Determinante der Koeffizientenmatrix
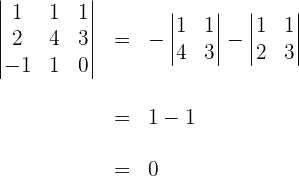
3 Da 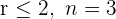 , stellen wir mit dem Satz von Kronecker-Capelli fest, dass das System mehrdeutig lösbar ist und unendlich viele Lösungen hat.
, stellen wir mit dem Satz von Kronecker-Capelli fest, dass das System mehrdeutig lösbar ist und unendlich viele Lösungen hat.
4 Wir berechnen die Lösungen. Hierzu wenden wir das Gaußsche Eliminationsverfahren an. Wir ersetzen die Zeilen 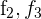 durch
durch 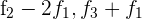
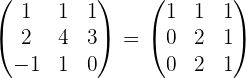
Wir ersetzen die Zeile 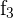 durch
durch 
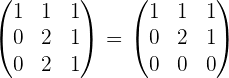
Wir erhalten ein äquivalentes Gleichungssystem
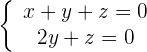
Wir setzen 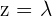 und erhalten
und erhalten
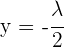 .
.
Wir setzen die Werte für 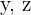 in die erste Gleichung ein und erhalten
in die erste Gleichung ein und erhalten
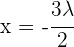 .
.
Die Lösungen haben die Form 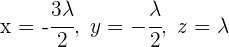
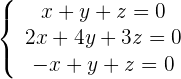
1 Wir bilden die Koeffizientenmatrix.
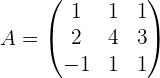
2 Wir berechnen die Determinante der Koeffizientenmatrix
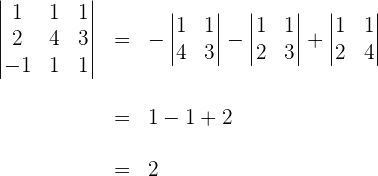
3 Da 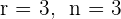 , stellen wir mit dem Satz von Kronecker-Capelli fest, dass das System eindeutig lösbar ist und eine eindeutige Lösung hat. Die Lösung ist
, stellen wir mit dem Satz von Kronecker-Capelli fest, dass das System eindeutig lösbar ist und eine eindeutige Lösung hat. Die Lösung ist 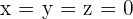 .
.
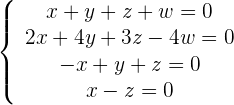
1 Wir bilden die Koeffizientenmatrix.
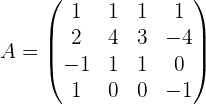
2 Wir berechnen die Determinante der Koeffizientenmatrix
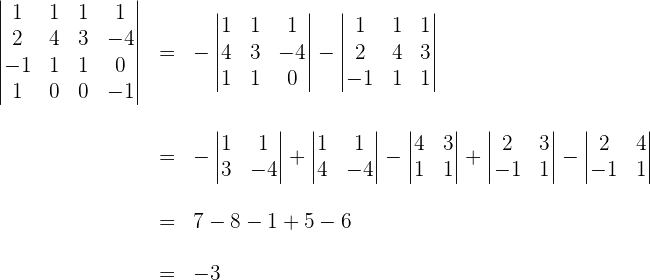
3 Da 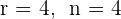 , stellen wir mit dem Satz von Kronecker-Capelli fest, dass das System eindeutig lösbar ist und eine eindeutige Lösung hat. Die Lösung ist
, stellen wir mit dem Satz von Kronecker-Capelli fest, dass das System eindeutig lösbar ist und eine eindeutige Lösung hat. Die Lösung ist 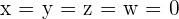 .
.
Mit KI zusammenfassen:













