Löse die folgenden Gleichungssysteme mit dem Additionsverfahren. Fall eine der Lösungen ein Bruch sein sollte, schreibe sie in der Form a/b.
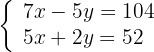
x =
y=
Dieses Feld ist erforderlich.
Wir eliminieren die Unbekannte  und somit:
und somit:
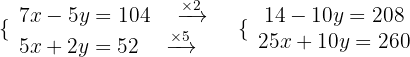
Nun addieren wir die Gleichungen
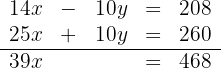
und erhalten die Unbekannte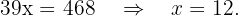
Zum Schluss berechnen wir die fehlende Unbekannte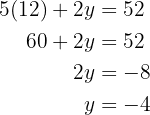
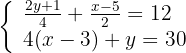
x=
y=
Dieses Feld ist erforderlich.
Wir beginnen, indem wir die Nenner der 1. Gleichung eliminieren:
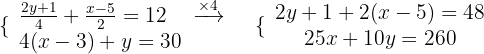
Wir vereinfachen:
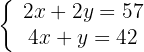
Wir eliminieren die Unbekannte  :
:
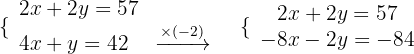
Wir addieren die Gleichungen
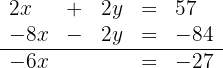
Somit sind die Unbekannten 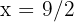 und
und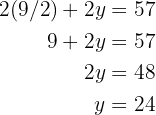
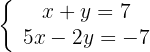
x=
y=
Dieses Feld ist erforderlich.
Wir eliminieren die Unbekannte  :
:
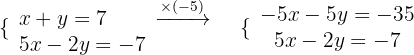
Wir addieren die Gleichungen
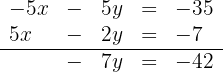
Somit sind die Unbekannten 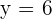 und
und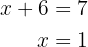
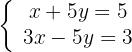
x=
y=
Dieses Feld ist erforderlich.
Wir eliminieren die Unbekannte  :
:
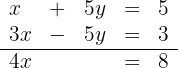
Somit sind die Unbekannten  und
und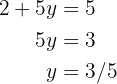
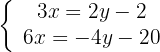
x=
y=
Dieses Feld ist erforderlich.
Wir eliminieren die Unbekannte  :
:
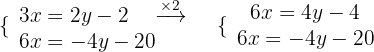
Wir addieren die Gleichungen
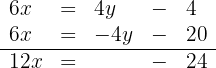
Somit sind die Unbekannten  und
und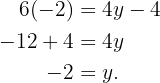
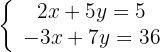
x=
y=
Dieses Feld ist erforderlich.
Wir eliminieren die Unbekannte  :
:
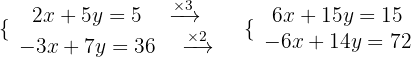
Wir addieren die Gleichungen
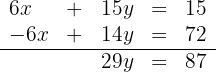
Somit sind die Unbekannten 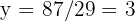 und
und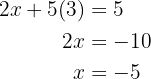
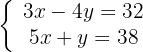
x=
y=
Dieses Feld ist erforderlich.
Wir eliminieren die Unbekannte  :
:
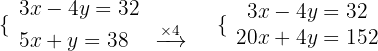
Wir addieren die Gleichungen
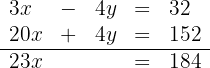
Somit sind die Unbekannten 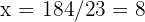 und
und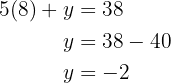
Löse die folgenden Problemstellungen:
In einem Gymnasium gibt es  Lehrer*innen, die auf zwei Gebäude, A und B, verteilt sind.
Lehrer*innen, die auf zwei Gebäude, A und B, verteilt sind.  % der Lehrer*innen in Gebäude A und
% der Lehrer*innen in Gebäude A und  % der Lehrer*innen in Gebäude B sind Männer, insgesamt also
% der Lehrer*innen in Gebäude B sind Männer, insgesamt also  Lehrer. Wie viele Lehrer*innen gibt es in jedem Gebäude?
Lehrer. Wie viele Lehrer*innen gibt es in jedem Gebäude?
Gebäude A: Lehrer*innen;
Gebäude B: Lehrer*innen.
Dieses Feld ist erforderlich.
Wir wählen zunächst die Unbekannten.
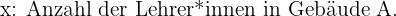
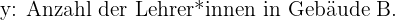
Mit diesen Werten erhalten wir die entsprechenden Gleichungen:
Insgesamt gibt es  Lehrer*innen, weshalb
Lehrer*innen, weshalb 
Andererseits sind  % der Lehrer*innen von Gebäude A plus
% der Lehrer*innen von Gebäude A plus  % der Lehrer*innen von Gebäude B Männer. Also insgesamt
% der Lehrer*innen von Gebäude B Männer. Also insgesamt  Personen. Somit ist
Personen. Somit ist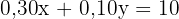
Wir erhalten folgende Gleichungen
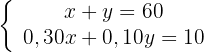
Wir lösen
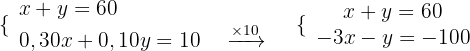
Wir addieren die Gleichungen
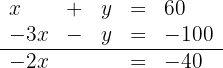
Daraus erhalten wir  . Wir setzen ein und erhalten
. Wir setzen ein und erhalten  .
.
Das heißt, dass sich in Gebäude A 20 und in Gebäude B 40 Lehrer*innen befinden.
Berechne eine Zahl, deren Ziffern sumiert 11 ergeben, und wobei bekannt ist, dass diese Zahl minus 27 dieselbe Zahl in umgekehrter Reihenfolge ergibt..
Dieses Feld ist erforderlich.
Wir wählen die Unbekannten
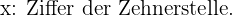
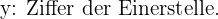
Wir erhalten die Gleichungen, indem wir die Angaben miteinander in Beziehung setzen. Zunächst ist die Summe der beiden Zahlen 11, daher gilt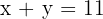
Die Zahl minus 27 ergibt die gesuchte Zahl mit umgekehrten Ziffern, also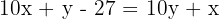
oder aber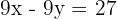
Wir lösen
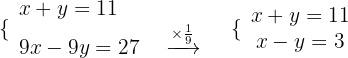
Wir addieren die Gleichungen
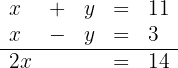
Daraus folgt, dass  . Wir setzen ein und erhalten
. Wir setzen ein und erhalten  .
.
Die Zehnerstelle ist also 7 und die Einerstelle ist 4, d. h. die gesuchte Zahl ist 74.
Kai und Daniel nehmen an einem Rennen teil. Es ist bekannt, dass ihre durchschnittliche Höchstgeschwindigkeit 520 km/h beträgt und dass die Höchstgeschwindigkeit von Daniel 80 km/h höher ist als die von Kai. Wie hoch sind ihre Höchstgeschwindigkeiten?
Maximale Geschwindigkeit von Kai km/hr;
Maximale Geschwindigkeit von Daniel km/hr.
Dieses Feld ist erforderlich.
Wir wählen die Unbekannten.
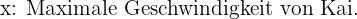
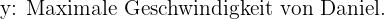
Wir erhalten die entsprechenden Gleichungen. Der Durschnitt der beiden Geschwindigkeiten liegt bei 260 km/hr, also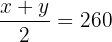
oder aber
und außerdem beträgt die Maximalgeschwindigkeit von Daniel 80 km/hr mehr als die Maximalgeschwindigkeit von Kai. Somit: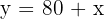
oder aber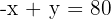
Wir lösen
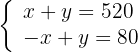
Wir addieren die Gleichungen
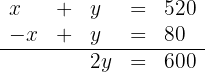
Daraus folgt, dass  . Wir setzen ein und erhalten
. Wir setzen ein und erhalten 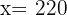 .
.
Lukas und sein Vater sind 25 Jahre auseinander. Berechne das Alter von Lukas, wenn du weißt, dass sein Vater in 15 Jahren doppelt so alt sein wird wie er.
Alter Lukas Jahre;
Alter seines Vaters .
Dieses Feld ist erforderlich.
Wir wählen die Unbekannten.
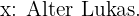
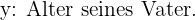
Wir erhalten die entsprechenden Gleichungen. Da Lukas und sein Vater 25 Jahre auseinander sind, ist
innerhalb von 15 Jahren wird das Alter von Lukas de 15 años la edad de Alberto será  und das Alter seines Vaters
und das Alter seines Vaters 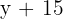 sein. Außerdem wird sein Vater doppelt so alt sein und somit
sein. Außerdem wird sein Vater doppelt so alt sein und somit
Wir lösen
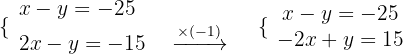
Wir addieren die Gleichungen
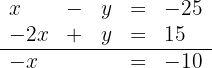
Daraus folgt, dass 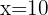 . Wir setzen ein und erhalten
. Wir setzen ein und erhalten  .
.
Mit KI zusammenfassen:


