
Konzept der Kombinationen mit Wiederholung
Kombinationen mit Wiederholung von m Elementen aus  in
in 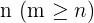 sind die verschiedenen Gruppen, die aus n Elementen gebildet werden, sodass:
sind die verschiedenen Gruppen, die aus n Elementen gebildet werden, sodass:
Nicht alle Elemente sind enthalten.
Die Reihenfolge spielt keine Rolle.
Die Elemente wiederholen sich.
Die Anzahl der Kombinationen mit Wiederholung wird mit 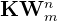 angegeben. Das Problem besteht nun darin, den Wert von
angegeben. Das Problem besteht nun darin, den Wert von 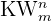 zu bestimmen, den wir mit der folgenden Formel berechnen können:
zu bestimmen, den wir mit der folgenden Formel berechnen können:
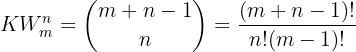
Die Zahl 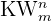 wird auch durch das Symbol
wird auch durch das Symbol 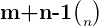 dargestellt. Bei Verwendung dieser Notation wird diese Zahl als Binomialkoeffizient bezeichnet.
dargestellt. Bei Verwendung dieser Notation wird diese Zahl als Binomialkoeffizient bezeichnet.
Beispiel für Kombinationen mit Wiederholung
In einem Weinkeller gibt es fünf verschiedene Arten von Flaschen. Auf wie viele Arten kann man vier Flaschen auswählen?
Lösung:
Nicht alle Elemente sind enthalten. Es werden nur  gewählt.
gewählt.
Die Reihenfolge spielt keine Rolle. Es spielt keine Rolle, ob  Flaschen Rotwein und
Flaschen Rotwein und  Flaschen Weißwein oder
Flaschen Weißwein oder  Flaschen Weißwein und
Flaschen Weißwein und  Flaschen Rotwein gewählt werde.
Flaschen Rotwein gewählt werde.
Die Elemente wiederholen sich. Es können mehrere Flaschen desselben Typs ausgewählt werden..
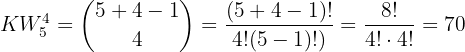
Mit KI zusammenfassen:












