Kapitel
Lösen nach Einsetzungsverfahren und grafischer Methode
Löse das folgende Gleichungssystem mithilfe des Einsetzungsverfahrens und der grafischen Methode.
1 Beginne mit der Andwendung des Einsetzungsverfahrens:
Beim Einsetzungsverfahren löst man nach einer der in der ersten Gleichung vorkommenden Variablen auf und setzt das Ergebnis in die zweite Gleichung ein. Löse nach 
aus der zweiten Gleichung auf
Hier wählt man am Besten die zweite Gleichung, da diese gleich Null ist; das macht den Vorgang etwas einfacher. Setze nun den Wert von in die erste Gleichung ein
Das heißt, 
. Setze nun den Wert von 
in den für erhaltenen Term ein:
Als Lösung erhält man folglich 
.
2 Löse das Gleichungssystem nun mithilfe der grafischen Methode:
Bei der grafischen Methode werden die beiden Geraden in einem Koordinatensystem visuell dargestellt. Um die Gleichung zu lösen, muss der Schnittpunkt der beiden Geraden ermittelt werden:
imagen
Die Grafik zeigt, dass die Lösung 
und ist. Denke daran, bei der Zeichnung der Grafik sehr genau vorzugehen.
Löse das folgende Gleichungssystem mithilfe des Einsetzungsverfahrens:
Ein Vorteil des Einsetzungsverfahrens ist, dass die Gleichung nicht vereinfacht werden muss, um die Variable zu berechnen. Das heißt, sie kann ohne Umwege gelöst werden.
Ermittle zuerst den Wert von aus der zweiten Gleichung:
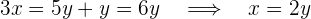
Setze nun den Wert von in die erste Gleichung ein:
Du erhältst 
. Setze nun den Wert von in den für ermittelten Term ein:
Die Lösung der Gleichung ist folglich und .
Lösen nach Gleichsetzungsverfahren
Zur Erinnerung: das Gleichsetzungsverfahren kann nur dann verwendet werden, wenn ein Gleichungssystem aus zwei Gleichungen mit zwei Variablen gelöst werden soll. Diese Methode sowie die grafische Methode sind auf 
-Gleichungssysteme beschränkt.
Löse das folgende Gleichungssystem mithilfe des Gleichsetzungsverfahrens:
Um das Gleichungssystem durch Gleichsetzen zu lösen, muss im ersten Schritt in beiden Gleichungen nach derselben Variable aufgelöst werden. Löse in beiden Gleichungen nach auf:
folglich ist 
. Für die zweite Gleichung ergibt sich
folglich ist 
y 
. Setze nun beide Gleichungen miteinander gleich
Löse in dieser Gleichung nach auf:
folglich ist . Setze nun den Wert von in die erste Gleichung ein
folglich ist . Die Lösung ist folglich y .
Löse das folgende Gleichungssystem mithilfe des Gleichsetzungsverfahrens:
Wie im vorherigen Beispiel muss zuerst in beiden Gleichungen nach derselben Variable aufgelöst werden. Löse in diesem Fall nach auf. Für die erste Gleichung erhältst du:
Für die zweite Gleichung erhältst du:
Setze nun die beiden Gleichungen miteinander gleich
folglich ist
das heißt 
. Setze den Wert von in die erste Gleichung ein und du erhältst
folglich ist . Die Lösungen sind daher y .
Lösen nach Reduktionsverfahren
Zur Erinnerung: beim Reduktionsverfahren müssen alle Variablen aus allen Gleichungen mit Ausnahme der ersten Gleichung eliminiert werden. Anschließend müssen in allen Gleichungen mit Ausnahme der ersten und zweiten Gleichung alle Variablen eliminiert werden.
Diese Methode entspricht dem Gaußschen Eliminationsverfahren, mit dem einzigen Unterschied, dass die dem Gleichungssystem zugehörige Matrix nicht verwendet wird.
Löse das folgende Gleichungssystem mithilfe des Reduktionsverfahrens:
Im ersten Schritt müssen alle der zweiten Gleichung eliminiert werden. Multipliziere die erste Gleichung dafür mit 
und ziehe das Ergebnis von der zweiten Gleichung ab:
Setze nun die vorherige Gleichung mit der zweiten Gleichung gleich:
folglich ist . Setze den Wert von in die erste Gleichung ein:
Folglich ist .
Man sieht, dass es sich um dasselbe Gleichungssystem wie in der vorherigen Aufgabe handelt und dass man trotz unterschiedlichem Lösungsweg zum selben Ergebnis kommt.
Löse das folgende Gleichungssystem mithilfe des Reduktionsverfahrens:
Bevor das Reduktionsverfahren angewendet werden kann, muss das Gleichungssystem so umgeschrieben werden, dass alle unabhängigen Terme auf der rechten Seite stehen. Multipliziere dafür beide Gleichungen mit 2:
Bringe nun alle Variablen auf die linke Seite:
Addiere die erste mit der zweiten Gleichung:
Folglich ist 
. Setze den Wert von in die erste Gleichung ein:
Als Lösung erhält man 
und .
Lösen nach einer beliebigen Methode
Löse das folgende Gleichungssystem nach der Methode deiner Wahl:
Das Gleichungssystem kann durch Einsetzen gelöst werden. Löse dafür die zweite Gleichung nach auf
Setze nun den Wert von in die erste Gleichung ein:
Durch umschreiben der unabhängigen Terme auf die rechte Seite und der Variablen auf die linke, sieht die Gleichung nun wie folgt aus:
durch Auflösen nach erhält man
Setze nun den Wert von in den Term ein, den du für ermittelt hast und du erhältst
Die Lösung ist folglich 
y 
Finde die Lösungen des folgenden Gleichungssystems:
Um dieses Gleichungssystem zu lösen, müssen zuerst die Brüche durch Auflösen der Nenner eliminiert werden. Multipliziere hierfür mit dem kleinsten gemeinsamen Vielfachen der Nenner. Für die erste Gleichung erhältst du:
folglich ist 
. Für die zweite Gleichung ergibt sich:
und folglich 
.Das Gleichungssystem sieht nun wie folgt aus:
Löse nun nach einer Methode deiner Wahl auf. Wir verwenden das Einsetzungsverfahren. Zuerst lösen wir in der zweiten Gleichung nach auf:
Dann setzen wir den Wert von in die erste Gleichung ein:
folglich ergibt sich
oder 
. Nun setzen wir den Wert von in den für erhaltenen Term ein:
Die Lösung ist daher 
y .
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
