
Unter- und überbestimmte lineare Gleichungssysteme
Entscheide, ob die folgende Aussage richtig oder falsch ist:
Wenn man eine Gleichung aus einem unterbestimmten LGS löscht, ist das neue LGS äquivalent zum ursprünglichen.
Richtig
Gegeben sei das lineare Gleichungssystem
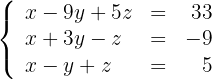
Schreibe das LGS in eine Matrix um. Ersetze die Zeilen  mit
mit 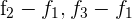 und du erhältst
und du erhältst
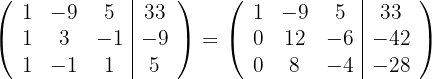
Ersetze die Zeile  mit
mit  und du erhältst
und du erhältst
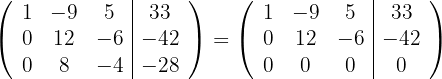
Das äquivalente LGS ist
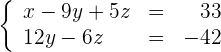
Die Lösung des unterbestimmten LGS ist
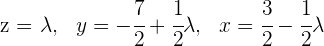
Entscheide, ob die folgende Aussage richtig oder falsch ist:
Ein unterbestimmtes LGS wird auch homogenes LGS genannt.
Falsch
Ein homogenes LGS besitzt im Allgemeinen nur die triviale Lösung:
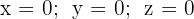 ,
,
während ein unterbestimmtes LGS unendlich viele Lösungen besitzen kann.
Entscheide, ob die folgende Aussage richtig oder falsch ist:
Jedes unterbestimmte LGS mit widerspruchsfreien Lösungen enthält zwei gleiche Gleichungen.
Falsch
Das unterbestimmte LGS
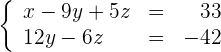
ist widerspruchsfrei und enthält nur unterschiedliche Gleichungen. Die Lösung des unterbestimmten LGS ist
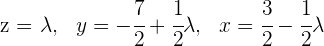
Entscheide, ob die folgende Aussage richtig oder falsch ist:
Aus einem überbestimmten LGS kann ein (nicht äquivalentes) unterbestimmtes LGS extrahiert werden, indem man Gleichungen entfernt.
Richtig
Gegeben sei das lineare Gleichungssystem
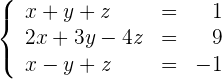
Schreibe das LGS in eine Matrix um. Ersetze die Zeilen  mit
mit 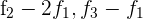 und du erhältst
und du erhältst
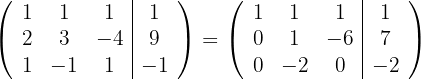
Die Lösung des überbestimmten LGS ist

Durch Eliminieren der zweiten Gleichung des ursprünglichen überbestimmten LGS erhält man das unterbestimmte LGS

mit der Lösung
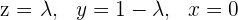
Finde heraus, um was für eine Art von LGS es sich im Folgenden handelt und ermittle seine Lösung(en) (wenn vorhanden)
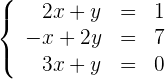
1
Schreibe das LGS in eine Matrix um. Ersetze die Zeilen  mit
mit 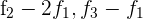 und du erhältst
und du erhältst
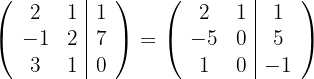
2
Ersetze die Zeile  mit
mit 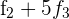 und du erhältst
und du erhältst
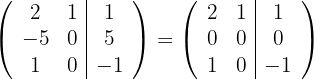
Die Lösung des überbestimmten LGS ist

Finde heraus, um was für eine Art von LGS es sich im Folgenden handelt und ermittle seine Lösung(en) (wenn vorhanden)
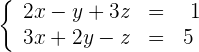
1
Schreibe das LGS in eine Matrix um. Ersetze die Zeile  mit
mit 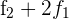 und du erhältst
und du erhältst
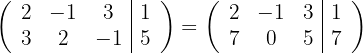
2
Definiere 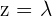 und setze diesen Wert in die beiden Gleichungen ein
und setze diesen Wert in die beiden Gleichungen ein
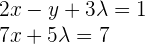
3
Die Lösung des unterbestimmten LGS ist

Löse das folgende Gleichungssystem:
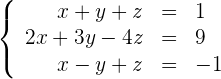
1
Schreibe das LGS in eine Matrix um. Ersetze die Zeilen  mit
mit 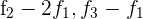 und du erhältst
und du erhältst
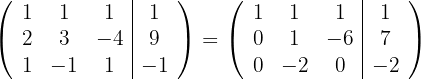
2
Aus der vorhergehenden Matrix erhält man
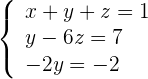
3
Aus der dritten Gleichung ergibt sich
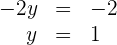
4
Setze den Wert von  in die zweite Gleichung ein und du erhältst
in die zweite Gleichung ein und du erhältst

5
Setze die Werte von 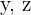 in die erste Gleichung ein und du erhältst
in die erste Gleichung ein und du erhältst

6
Die Lösung des überbestimmten LGS ist
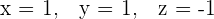
Löse das folgende Gleichungssystem:

1
Schreibe das LGS in eine Matrix um. Tausche die Zeilen  entsprechend mit
entsprechend mit 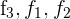 aus und du erhältst
aus und du erhältst
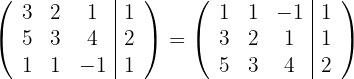
Ersetze die Zeilen  mit
mit 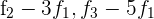 und du erhältst
und du erhältst
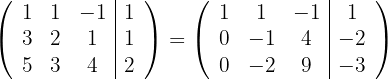
Ersetze die Zeile  mit
mit  und du erhältst
und du erhältst
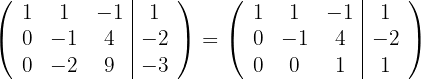
2
Aus der vorhergehenden Matrix erhält man

3
Setze den Wert von  in die zweite Gleichung ein und du erhältst
in die zweite Gleichung ein und du erhältst

4
Setze die Werte von 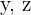 in die erste Gleichung ein und du erhältst
in die erste Gleichung ein und du erhältst
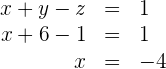
5
Die Lösung des überbestimmten LGS ist

Löse das folgende Gleichungssystem:
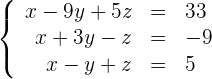
1
Schreibe das LGS in eine Matrix um. Ersetze die Zeilen  mit
mit  und du erhältst
und du erhältst
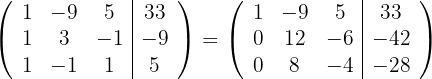
Ersetze die Zeile  mit
mit  und du erhältst
und du erhältst
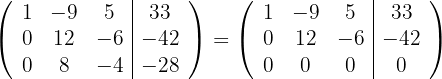
2
Aus der vorhergehenden Matrix erhält man

3
Definiere 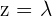 und setze den Wert in die zweite Gleichung ein
und setze den Wert in die zweite Gleichung ein
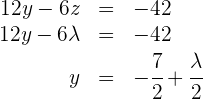
4
Setze die Werte von 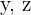 in die erste Gleichung ein und du erhältst
in die erste Gleichung ein und du erhältst
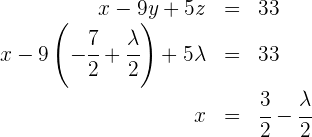
5
Die Lösung des unterbestimmten LGS ist
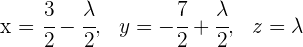
Löse das folgende Gleichungssystem

1
Schreibe das LGS in eine Matrix um. Ersetze die Zeilen 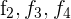 mit
mit 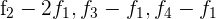 und du erhältst
und du erhältst
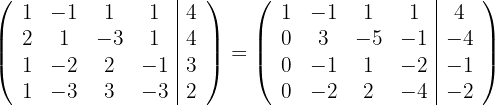
Ersetze die Zeilen 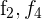 mit
mit  und du erhältst
und du erhältst
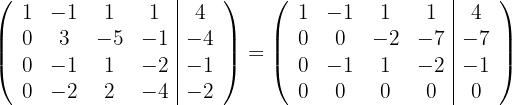
2
Aus der vorhergehenden Matrix erhält man
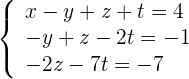
3
Definiere 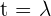 und setze den Wert in die dritte Gleichung ein
und setze den Wert in die dritte Gleichung ein
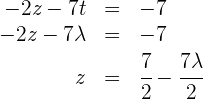
4
Setze die Werte von 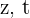 in die zweite Gleichung ein und du erhältst
in die zweite Gleichung ein und du erhältst
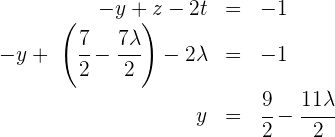
5
Setze die Werte von 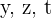 in die erste Gleichung ein und du erhältst
in die erste Gleichung ein und du erhältst
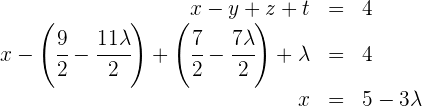
6
Die Lösung des unterbestimmten LGS ist
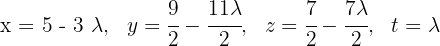
Löse das folgende Gleichungssystem
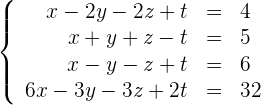
1
Schreibe das LGS in eine Matrix um. Ersetze die Zeilen  mit
mit 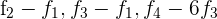 und du erhältst
und du erhältst
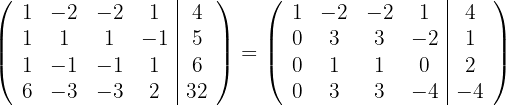
Ersetze die Zeilen 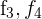 mit
mit 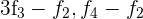 und du erhältst
und du erhältst
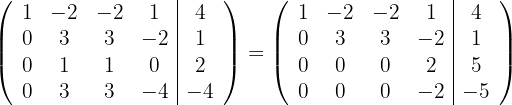
2
Die letzte Zeile der vorherigen Matrix ist ein Vielfaches der vorletzten, daher erhält man
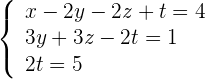
3
Aus der dritten Gleichung ergibt sich 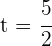 . Definiere
. Definiere 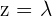 und setze den Wert in die zweite Gleichung ein
und setze den Wert in die zweite Gleichung ein

4
Setze die Werte von 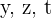 in die erste Gleichung ein und du erhältst
in die erste Gleichung ein und du erhältst
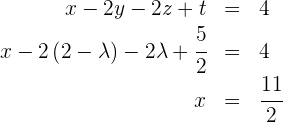
5
Die Lösung des unterbestimmten LGS ist

Löse das folgende Gleichungssystem:

1
Schreibe das LGS in eine Matrix um und tausche die Zeilen eins und zwei miteinander aus
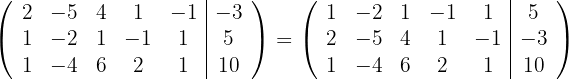
Ersetze die Zeilen 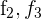 mit
mit 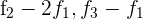 und du erhältst
und du erhältst
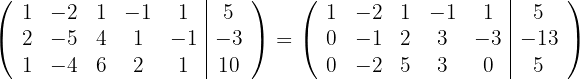
Ersetze die Zeile  mit
mit  und du erhältst
und du erhältst
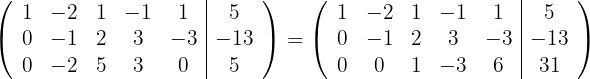
2
Man erhält ein äquivalentes Gleichungssystem
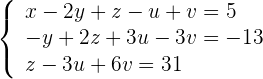
3
Definiere 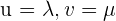 und setze den Wert in die dritte Gleichung ein
und setze den Wert in die dritte Gleichung ein

4
Setze die Werte von 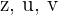 in die zweite Gleichung ein und du erhältst
in die zweite Gleichung ein und du erhältst

5
Setze die Werte von 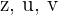 in die erste Gleichung ein und du erhältst
in die erste Gleichung ein und du erhältst

Löse das folgende Gleichungssystem:
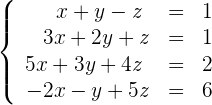
1
Schreibe das LGS in eine Matrix um. Ersetze die Zeilen 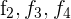 mit
mit 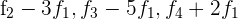 und du erhältst
und du erhältst
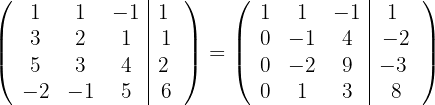
Ersetze die Zeilen 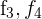 mit
mit 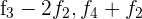 und du erhältst
und du erhältst
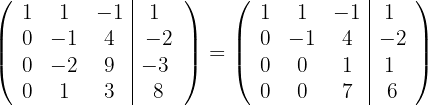
Ersetze die Zeile  mit
mit  und du erhältst
und du erhältst
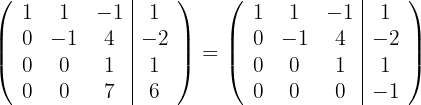
2
Aus der vorhergehenden Matrix lässt sich ablesen, dass das Gleichungssystem keine gültigen Lösungen besitzt.
Parameter bestimmen
Finde heraus, ob es einen Wert von  gibt, für den das Gleichungssystem Lösungen besitzt. Wenn es einen gibt, löse das Gleichungssystem für diesen Wert von
gibt, für den das Gleichungssystem Lösungen besitzt. Wenn es einen gibt, löse das Gleichungssystem für diesen Wert von  .
.
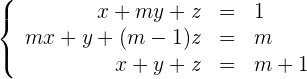
1
Schreibe das LGS in eine Matrix um. Ersetze die Zeilen  mit
mit 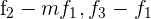 und du erhältst
und du erhältst
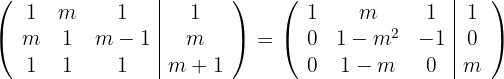
2
Die dritte Zeile zeigt, dass das LGS für 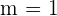 keine Lösungen vorliegen, da
keine Lösungen vorliegen, da 
3
Für  ist das überbestimmte LGS gleichwertig mit
ist das überbestimmte LGS gleichwertig mit
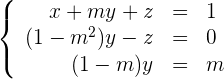
Die dritte Gleichung ergibt
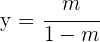
Setze den Wert von  in die zweite Gleichung ein und du erhältst
in die zweite Gleichung ein und du erhältst

Setze die Werte von 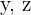 in die erste Gleichung ein und du erhältst
in die erste Gleichung ein und du erhältst
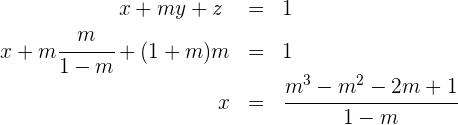
Parameter bestimmen
Finde heraus, ob es einen Wert von  gibt, für den das Gleichungssystem Lösungen besitzt. SWenn es einen gibt, löse das Gleichungssystem für diesen Wert von
gibt, für den das Gleichungssystem Lösungen besitzt. SWenn es einen gibt, löse das Gleichungssystem für diesen Wert von  .
.
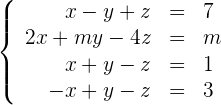
1
Schreibe das LGS in eine Matrix um. Ersetze die Zeile  mit
mit 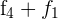
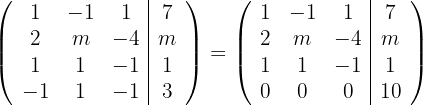
2
Die vierte Zeile zeigt, dass das LGS für keinen Wert von  Lösungen besitzt, da
Lösungen besitzt, da 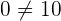
Parameter bestimmen
Bestimme die Lösung(en) des folgenden LGS für die Werte von 

1
Schreibe das LGS in eine Matrix um. Ersetze die Zeilen 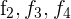 mit
mit 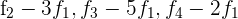 und du erhältst
und du erhältst
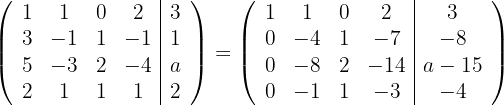
2
Ersetze die Zeilen  mit
mit 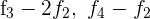 und du erhältst
und du erhältst
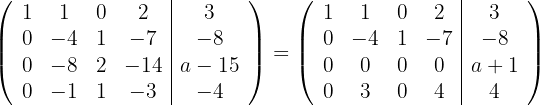
3
Die dritte Zeile zeigt, dass das LGS für 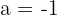 unterbestimmt ist, da
unterbestimmt ist, da 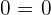
4
Für  besitzt das LGS keine Lösungen.
besitzt das LGS keine Lösungen.
Parameter bestimmen
Bestimme die Lösung(en) des folgenden LGS für die Werte von  und
und 
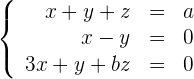
1
Schreibe das LGS in eine Matrix um. Ersetze die Zeilen 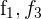 mit
mit 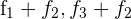 und du erhältst
und du erhältst
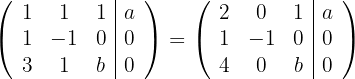
2
Ersetze die Zeile  mit
mit 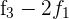 und du erhältst
und du erhältst
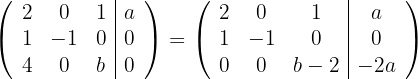
3
Die dritte Zeile zeigt:
für  und
und 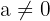 , besitzt das LGS keine Lösungen
, besitzt das LGS keine Lösungen
für  und
und 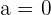 ist das LGS unterbestimmt;
ist das LGS unterbestimmt;
für 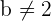 ist das LGS für jeden Wert von
ist das LGS für jeden Wert von  überbestimmt.
überbestimmt.
Parameter bestimmen
Bestimme, für welche Werte von  das folgende LGS unendlich viele Lösungen besitzt
das folgende LGS unendlich viele Lösungen besitzt
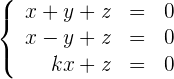
1
Schreibe das LGS in eine Matrix um. Ersetze die Zeile  mit
mit 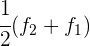 und du erhältst
und du erhältst
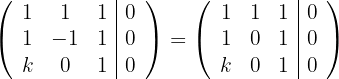
2
Ersetze die Zeile  mit
mit  und du erhältst
und du erhältst
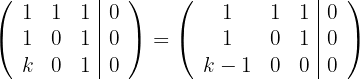
3
Die dritte Zeile zeigt, dass das LGS für 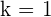 unterbestimmt ist, d.h. unendlich viele Lösungen besitzt.
unterbestimmt ist, d.h. unendlich viele Lösungen besitzt.
Der Besitzer eines Lokals hat Softdrinks, Bier und Wein im Wert von  € (netto) eingekauft. Für den Wein hat er
€ (netto) eingekauft. Für den Wein hat er  € weniger als für die Softdrinks und das Bier zusammen bezahlt. Berechne, wie viel er für jede Art von Getränk bezahlt hat und beachte dabei, dass die Mehrwertsteuer für die Softdrinks
€ weniger als für die Softdrinks und das Bier zusammen bezahlt. Berechne, wie viel er für jede Art von Getränk bezahlt hat und beachte dabei, dass die Mehrwertsteuer für die Softdrinks 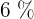 , für das Bier
, für das Bier 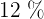 und für den Wein
und für den Wein  beträgt, sodass sich eine Rechnung von insgesamt
beträgt, sodass sich eine Rechnung von insgesamt 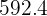 € inkl. Mehrwertsteuer ergibt.
€ inkl. Mehrwertsteuer ergibt.
1
Stelle anhand der Variablen  die Beträge für Softdrinks, Bier und Wein in € dar. Definiere die zugrundeliegenden Bedingungen anhand von Gleichungen
die Beträge für Softdrinks, Bier und Wein in € dar. Definiere die zugrundeliegenden Bedingungen anhand von Gleichungen
Der Besitzer eines Lokals hat Softdrinks, Bier und Wein im Wert von  € (netto) eingekauft.
€ (netto) eingekauft.
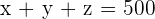
Für den Wein hat er  € weniger als für die Softdrinks und das Bier zusammen bezahlt.
€ weniger als für die Softdrinks und das Bier zusammen bezahlt.
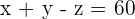
Beachte, dass die Mehrwertsteuer für die Softdrinks 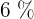 , für das Bier
, für das Bier 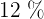 und für den Wein
und für den Wein  beträgt, sodass sich eine Rechnung von insgesamt
beträgt, sodass sich eine Rechnung von insgesamt 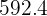 € inkl. Mehrwertsteuer ergibt. €
€ inkl. Mehrwertsteuer ergibt. €
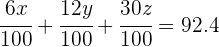
Multipliziere beide Seiten der Gleichung mit 

2
Man erhält das folgende Gleichungssystem

3
Schreibe die drei Gleichungen in eine Matrix um. Ersetze die Zeilen  mit
mit 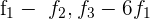 und du erhältst
und du erhältst
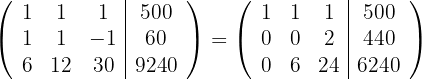
4
Das überbestimmte LGS ist äquivalent zu
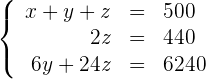
Die zweite Gleichung ergibt
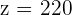
Setze den Wert von  in die dritte Gleichung ein und du erhältst
in die dritte Gleichung ein und du erhältst
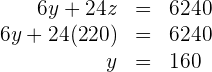
Setze die Werte von 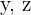 in die erste Gleichung ein und du erhältst
in die erste Gleichung ein und du erhältst
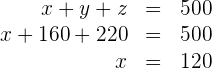
5
Die Lösungen sind  €,
€,  €,
€, 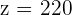 €.
€.
Ein Unternehmen besitzt drei Bergwerke mit Erzen unterschiedlicher Zusammensetzung:
| Nickel (%) | Kupfer (%) | Eisen (%) | |
|---|---|---|---|
| Bergwerk A | 1 | 2 | 3 |
| Bergwerk B | 2 | 5 | 7 |
| Bergwerk C | 1 | 3 | 1 |
Wei viele Tonnen werden aus jedem Bergwerk benötigt, um 7 Tonnen Nickel, 18 Tonnen Kupfer und 16 Tonnen Eisen zu erzeugen?
1
Stelle anhand der Variablen  die Anzahl der Tonnen der Minen A, B und C dar. Definiere die zugrundeliegenden Bedingungen anhand von Gleichungen:
die Anzahl der Tonnen der Minen A, B und C dar. Definiere die zugrundeliegenden Bedingungen anhand von Gleichungen:

2
Schreibe die drei Gleichungen in eine Matrix um. Ersetze die Zeilen  mit
mit  und du erhältst
und du erhältst
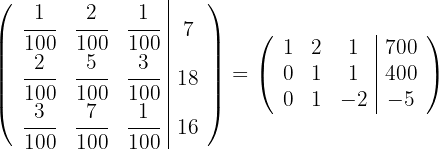
Ersetze die Zeile  mit
mit  und du erhältst
und du erhältst
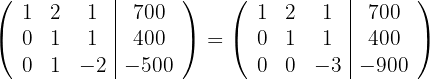
3
Das überbestimmte LGS ist äquivalent zu
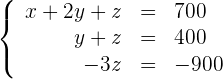
Die dritte Gleichung ergibt
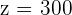
Setze den Wert von  in die zweite Gleichung ein und du erhältst
in die zweite Gleichung ein und du erhältst
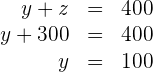
Setze die Werte von 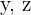 in die erste Gleichung ein und du erhältst
in die erste Gleichung ein und du erhältst
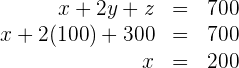
Ein Vater ist doppelt so alt wie das Alter seiner beiden Kinder zusammen. Vor wenigen Jahren (genauer gesagt vor so vielen Jahren, wie die Differenz des aktuellen Alters der beiden Kinder ergibt), war der Vater dreimal so alt wie seine beiden Kinder damals zum damaligen Zeitpunkt. Wenn so viele Jahre wie die Summe des aktuellen Alters der beiden Kinder vorbeigegangen sind, sind die drei Personen zusammen 150 Jahre alt. Wie alt war der Vater, als seine beiden Kinder geboren wurden?
1
Stelle anhand der Variablen  das aktuelle Alter des Vaters sowie des älteren und des jüngeren Kindes dar. Definiere die zugrundeliegenden Bedingungen anhand von Gleichungen
das aktuelle Alter des Vaters sowie des älteren und des jüngeren Kindes dar. Definiere die zugrundeliegenden Bedingungen anhand von Gleichungen
Ein Vater ist doppelt so alt wie das Alter seiner beiden Kinder zusammen.

Vor wenigen Jahren (genauer gesagt vor so vielen Jahren, wie die Differenz des aktuellen Alters der beiden Kinder ergibt), war der Vater dreimal so alt wie seine beiden Kinder damals zum damaligen Zeitpunkt.
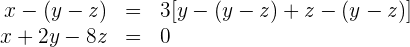
Wenn so viele Jahre wie die Summe des aktuellen Alters der beiden Kinder vorbeigegangen sind, sind die drei Personen zusammen 150 Jahre alt.

2
Man erhält das folgende Gleichungssystem
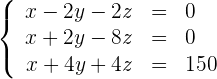
3
Schreibe die drei Gleichungen in eine Matrix um. Ersetze die Zeilen  mit
mit 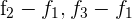 und du erhältst
und du erhältst
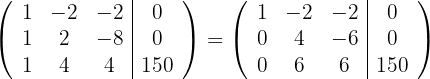
Ersetze die Zeile  mit
mit 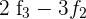 und du erhältst
und du erhältst
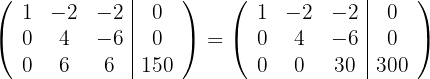
4
Das überbestimmte LGS ist äquivalent zu
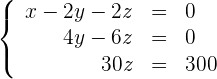
Die dritte Gleichung ergibt
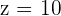
Setze den Wert von  in die zweite Gleichung ein und du erhältst
in die zweite Gleichung ein und du erhältst
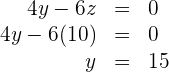
Setze die Werte von 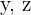 in die erste Gleichung ein und du erhältst
in die erste Gleichung ein und du erhältst

5
Der Vater war bei der Geburt seiner Kinder 35 und 40 Jahre alt.
Mit KI zusammenfassen:













