Kapitel
Aufgaben zur Berechnung von Flächeninhalt und Umfang
Wie groß ist der Flächeninhalt eines Rechtecks, dessen Umfang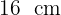 
beträgt und dessen Grundseite dreimal so lang wie seine Höhe ist?
1 Definiere die Variablen
Grundseite des Rechtecks
Höhe des Rechtecks
2 Formuliere die Gleichungen
Umfang
3 Stelle das Gleichungssystem auf: lege die Beziehung zwischen Grundseite und Höhe in der ersten Gleichung fest und in der zweiten den Umfang
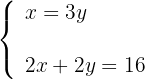
4 Setze den Wert von 
aus der ersten Gleichung in die zweite ein, um den Wert von
zu berechnen
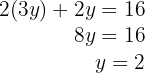
5 Setze das Ergebnis in die erste Gleichung ein, um den Wert von zu ermitteln
6 Die Grundseite misst also 
und die Höhe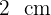 
Die Grundseite eines Dreiecks ist dreimal so lang wie seine Höhe. Wenn die Fläche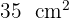 
beträgt, welche Maße hat das Dreieck?
1 Definiere die Variablen
Grundseite des Dreiecks
Höhe des Dreiecks
2 Formuliere die Gleichungen
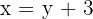
3 Stelle das Gleichungssystem auf: lege die Beziehung zwischen der Grundseite und der Höhe in der ersten Gleichung fest und in der zweiten den Umfang
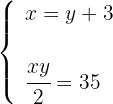
4 Setze den Wert von aus der ersten Gleichung in die zweite ein, um den Wert von zu berechnen
man erhält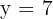 
(der Wert
wird nicht beachtet, da man kein negatives Ergebnis erhalten darf).
5 Setze das Ergebnis in die erste Gleichung ein, um den Wert von zu ermitteln
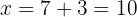
6 Die Grundseite misst also 
und die Höhe 
Rechenaufgaben am Beispiel Farm
Auf einer Farm werden Truthähne und Schweine gezüchtet. Insgesamt kann man dort 
Köpfe und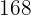 
Beine zählen. Wie viele Truthähne und Schweine gibt es dort?
1 Definiere die Variablen
Anzahl der Truthähne
Anzahl der Schweine
2 Stelle die Gleichungen auf, indem du die Parameter für die Anzahl der Köpfe und für die Anzahl der Beine festlegst.
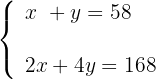
3 Löse das Gleichungssystem durch Reduktion, indem du die erste Gleichung mit -2 multiplizierst
4 Setze den Wert von in die erste Gleichung ein, um den Wert von zu ermitteln
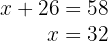
5 Es gibt also 
Truthähne und 
Schweine auf der Farm.
Peter und Jörg züchten Truthähne. Jörg sagt: wenn du mir 
Truthähne gibst, haben wir gleich viele; Peter antwortet: wenn du mir Truthähne gibst, hätte ich danach dreimal mehr als du. Wie viele Truthähne besitzt jeder?
1 Definiere die Variablen
Anzahl der Truthähne von Peter
Anzahl der Truthähne von Jörg
2 Formuliere die Gleichungen
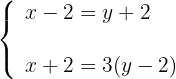
3 Stelle in der ersten Gleichung frei und setze den Wert in die zweite Gleichung ein
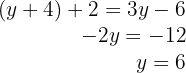
4 Setze den Wert von in die erste Gleichung ein, um den Wert von zu ermitteln
5 Peter hat 
Truthähne und Jörg 
.
Martha geht auf den Wochenmarkt und kauft 
Äpfel und Orangen für 
€. Wenn sie Äpfel und Orangen gekauft hätte, hätte sie 
€ bezahlt. Wie viel kostet jede Frucht?
1 Definiere die Variablen
Preis für einen Apfel
Preis für eine Orange
2 Stelle das Gleichungsystem auf
3 Löse das Gleichungssystem durch Reduktion, indem du die erste Gleichung mit -2 und die zweite mit 3 multiplizierst
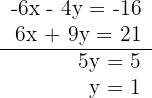
4 Berechne den Wert von , indem du den Wert von in die erste Gleichung einsetzt
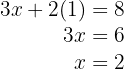
5 Ein Apfel kostet € und eine Orange 
€
Arithmetische Aufgaben
Die Zehnerstelle einer gesuchten zweistelligen Zahl ist das doppelte ihrer Einerstelle. Zieht man 
von der gesuchten Zahl ab, erhält man die Zahl, die sich aus der Umkehrung der Reihenfolge der Ziffern ergibt. Welche Zahl wird gesucht?
1 Definiere die Variablen
Ziffer der Einerstelle
Ziffer der Zehnerstelle
2 Stelle die Gleichung für die gesuchte Zahl auf
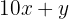
3 Stelle die Gleichung für Zahl mit umgekehrten Ziffern auf
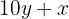
4 Stelle das Gleichungssystem auf
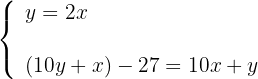
5 Setze den Wert von in die zweite Gleichung ein
6 Löse die Gleichung
7 Berechne den Wert von
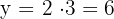
8 Die gesuchte Zahl ist 
Gesucht ist eine zweistellige Zahl, deren Zehlerstelle und Einerstelle zusammen 
ergeben. Zieht man von der gesuchten Zahl ab, erhält man die Zahl, die sich aus der Umkehrung der Reihenfolge der Ziffern ergibt.
1 Definiere die Variablen
Ziffer der Einerstelle
Ziffer der Zehnerstelle
2 Lege die Bedingungen fest
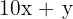= gesuchte Zahl
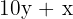= umgekehrte Zahl
3 Stelle das Gleichungssystem auf
4 Stelle in der ersten Gleichung frei und setze den Wert in die zweite Gleichung ein
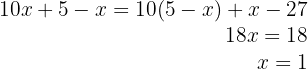
5 Setze den Wert von in die erste Gleichung ein
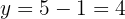
6 Gesucht ist die Zahl 
Rechenanwendungen im Kauf und Verkauf
Jürgen hat einen Computer und einen Fernseher für insgesamt 
€ gekauft und für 
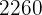€ wieder verkauft.
Wie viel hat jedes Gerät gekostet, wenn man beachtet, dass er beim Verkauf des Computers 
und beim Verkauf des Fernsehers 
verdient hat?
1 Definiere die Variablen
Preis des Computers
Preis des Fernsehers
2 Definiere die Verkaufspreise
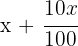
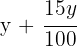
3 Stelle ein Gleichungssystem mit einer Gleichung für den Kauf und einer für den Verkauf auf
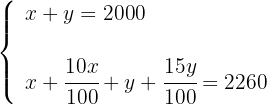
4 Löse die Nenner auf
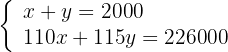
5 Löse das Gleichungssystem durch Reduktion, indem du die erste Gleichung mit -110 multiplizierst
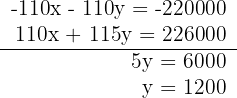
6 Setze den Wert von in die erste Gleichung ein
Der Computer hat also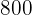 
€ und der Fernseher 
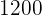€ gekostet.
Anton sagt zu Peter: "Ich habe doppelt so viel Geld wie du." Peter antwortet: "Wenn du mir 6€ gibst, haben wir beide gleichviel Geld." Wie viel Geld besitzt jeder?
1 Definiere die Variablen
Anton´s Geld
Peter´s Geld
2 Stelle das Gleichungssystem auf: halte in der ersten Gleichung fest, was Anton sagt und in der zweiten, was Peter sagt. Beachte dabei, dass er € weniger hat, wenn er € hergibt.
3 Setze den Wert von in die zweite Gleichung ein
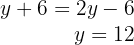
4 Berechne den Wert von in der ersten Gleichung
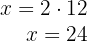
5 Anton hat also 
€ und Peter 
€.
In einem Unternehmen arbeiten 
Personen. 
der Männer und 
der Frauen tragen eine Brille. Wenn insgesamt 
Personen eine Brille tragen, wie viele Männer und Frauen arbeiten dann im Unternehmen?
1 Definiere die Variablen
Zahl der Männer
Zahl der Frauen
2 Lege die Bedingungen für die Zahl der männlichen und weiblichen Brillenträger
fest
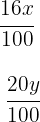
3 Stelle das Gleichungssystem auf
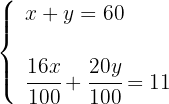
4 Löse die Nenner in der zweiten Gleichung auf
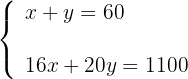
5 Löse das LGS mithilfe des Einsatzverfahrens, indem du in der ersten Gleichung freistellst/p>
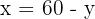
6 Setze den Wert von in die zweite Gleichung ein und löse
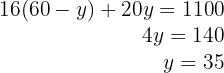
7 Setze den Wert von in die erste Gleichung ein
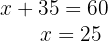
8 Es arbeiten folglich 
Männer und 
Frauen im Unternehmen.
Für den Kauf von zwei Haushaltsgeräten hast du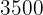 
€ bezahlt. Wenn wir auf das erste Gerät einen Rabatt von und auf das zweite einen Rabatt von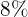 
erhalten hätten, hätten wir insgesamt 
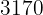€ bezahlt. Wie viel hat jedes Gerät gekostet?
1 Definiere die Variablen
Preis Gerät 1
Preis Gerät 2
2 Definiere die Konditionen der Rabatte
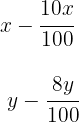
3 Stelle das Gleichungssystem auf
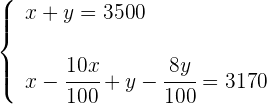
4 Löse die Nenner in der zweiten Gleichung auf
5 Löse das Gleichungssystem durch Reduktion, indem du die erste Gleichung mit -90 multiplizierst
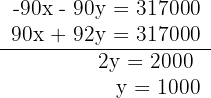
6 Berechne den Wert von , indem du den Wert von in die erste Gleichung einsetzt
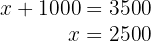
7 Gerät 1 hat also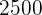 
€ gekostet, Gerät 2 
€.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
