Kapitel
Die Schnittmenge von Ereignissen 
ist das Ereignis, das aus allen Elementen besteht, die gleichzeitig zu 
und 
gehören.
Das Ereignis 
tritt ein, wenn und gleichzeitig eintreten.
Beispiel:
Betrachten wir das Experiment, bei dem ein Würfel geworfen wird, wobei 
eine gerade Zahl und 
ein Vielfaches von 3 gewürfelt wird. Berechne .
1 
2 
3 
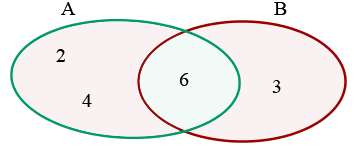
Eigenschaften der Schnittmenge von Ereignissen
1 Kommutativ
2 Assoziativ
3 Idempotent
4 Vereinfachung
5 Distributiv
6 Neutrales Element
7 Leere Menge
Wahrscheinlichkeit der Überschneidung von Ereignissen
Unabhängige Ereignisse
Zwei Ereignisse und sind unabhängig, wenn die Wahrscheinlichkeit, dass eintritt, nicht davon beeinflusst wird, ob eingetreten ist oder nicht.
Beispiel:
Man hat ein Kartenspiel mit 40 Karten, zieht eine Karte und legt sie wieder zurück. Wie hoch ist die Wahrscheinlichkeit, zwei Könige zu ziehen?
1 Das Ereignis besteht darin, einen König aus einem Kartenstapel mit 40 Karten zu ziehen. Da sich in dem Stapel 4 Könige befinden, haben wir
2 Wir legen die Karte zurück zum Stapel und haben wieder 40 Karten. Das Ereignis besteht darin, einen König aus dem Stapel mit 40 Karten zu ziehen.
3 Da das zweite Ereignis unabhängig vom ersten ist, haben wir
Abhängige Ereignisse
Zwei Ereignisse und sind abhängig, wenn die Wahrscheinlichkeit, dass eintritt, davon beeinflusst wird, ob eingetreten ist oder nicht.
Beispiel:
Man hat ein Kartenspiel mit 40 Karten und zieht zwei Karten. Wie hoch ist die Wahrscheinlichkeit, zwei Könige zu ziehen?
1 Das Ereignis besteht darin, einen König aus dem Kartenspiel mit 40 Karten zu ziehen. Da das Kartenspiel 4 Könige enthält, haben wir
2 Jetzt hat das Kartenspiel 39 Karten und darunter 3 Könige. Das Ereignis besteht darin, einen König aus dem Kartenspiel mit 39 Karten zu ziehen.
3 Da das zweite Ereignis vom ersten abhängig ist, haben wir
Mit KI zusammenfassen:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
