
Aufgaben zu Konkavität, Konvexität und Wendepunkten von Funktionen
Berechne die Intervalle des Monotonieverhaltens der Funktionen:
1 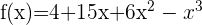
1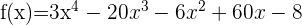
1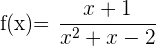
1
1
1
1 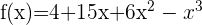 Zunächst wird die Ableitung der Funktion berechnet und gleich 0 gesetzt.
Zunächst wird die Ableitung der Funktion berechnet und gleich 0 gesetzt.

Die Nullstellen sind 
Wir unterteilen die Zahlengerade in 3 Intervalle: 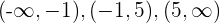 . Wir wählen einen Punkt eines jeden Intervalls und setzen ihn in
. Wir wählen einen Punkt eines jeden Intervalls und setzen ihn in 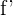 ein:
ein:
Ist das Ergebnis positiv, steigt die Funktion in diesem Intervall.
Ist das Ergebnis negativ, fällt die Funktion in diesem Intervall.
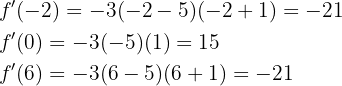
Die Funktion steigt also im Intervall  und fällt in den Intervallen
und fällt in den Intervallen 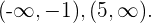
2 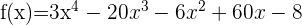
Zunächst wird die Ableitung der Funktion berechnet und gleich 0 gesetzt.

Die Nullstellen sind 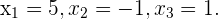
Wir unterteilen die Zahlengerade in 4 Intervalle:  . Wir wählen einen Punkt eines jeden Intervalls und setzen ihn in
. Wir wählen einen Punkt eines jeden Intervalls und setzen ihn in 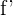 ein:
ein:
Ist das Ergebnis positiv, steigt die Funktion in diesem Intervall.
Ist das Ergebnis negativ, fällt die Funktion in diesem Intervall.
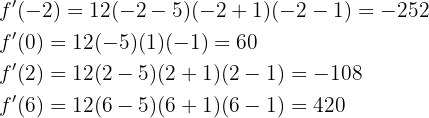
Die Funktion steigt also in den Intervallen  und fällt in den Intervallen
und fällt in den Intervallen 
3 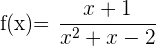
Die Berechnung der Nullstellen des Nenners ergibt die Werte, für die die Funktion nicht definiert ist.
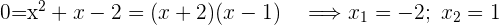
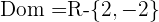
Wir leiten die Funktion ab und berechnen ihre Nullstellen.

Wir setzen die Ableitung gleich 0 und berechnen die Nullstellen des Zählers, die den Nullstellen der Funktion entsprechen.
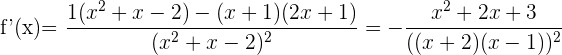
Sie hat keine Nullstellen in den reellen Zahlen, da die Diskriminante negativ ist:  Die Intervalle werden also anhand der Unstetigkeitsstellen gebildet:
Die Intervalle werden also anhand der Unstetigkeitsstellen gebildet: 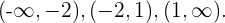 Wir wählen dann einen Punkt aus jedem Intervall und setzen ihn in
Wir wählen dann einen Punkt aus jedem Intervall und setzen ihn in 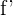 ein:
ein:
Ist das Ergebnis positiv, steigt die Funktion in diesem Intervall.
Ist das Ergebnis negativ, fällt die Funktion in diesem Intervall.
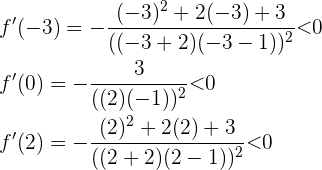
Die Funktion ist also immer fallend.
4 
Wir berechnen zunächst den Definitionsbereich, um zu wissen, wo die Funktion definiert ist.


Wir leiten ab:
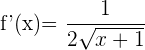
Da der Nenner den Wert 1 hat, besitzt die Ableitung keine Nullstellen. Wenn wir also an einem Punkt von 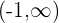 auswerten, sehen wir, dass der Graph steigt:
auswerten, sehen wir, dass der Graph steigt:
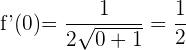
5 
Zunächst wird die Ableitung der Funktion berechnet und gleich 0 gesetzt.
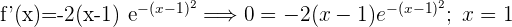
Ihre Nullstellen sind 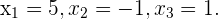
Wir unterteilen die Zahlengerade in 3 Intervalle: 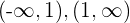 . Wir wählen dann einen Punkt aus jedem Intervall und setzen ihn in
. Wir wählen dann einen Punkt aus jedem Intervall und setzen ihn in 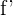 ein:
ein:
Ist das Ergebnis positiv, steigt die Funktion in diesem Intervall.
Ist das Ergebnis negativ, fällt die Funktion in diesem Intervall.
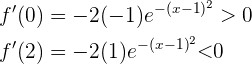
Die Funktion steigt also bei  und fällt bei
und fällt bei 
6 
Zunächst wird der Definitionsbereich berechnet, um zu wissen, wo die Funktion definiert ist.
Da die Logarithmusfunktion nur auf positive Zahlen angewendet werden kann, 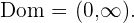
Nun leiten wir die Funktion ab:

Wenn wir 0 setzen und den Logarithmus bestimmen, erhalten wir die Nullstelle 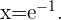 Wir teilen den Definitionsbereich in 2 Intervalle:
Wir teilen den Definitionsbereich in 2 Intervalle:  . Wir wählen dann einen Punkt aus jedem Intervall und setzen ihn in
. Wir wählen dann einen Punkt aus jedem Intervall und setzen ihn in 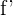 ein:
ein:
Ist das Ergebnis positiv, steigt die Funktion in diesem Intervall.
Ist das Ergebnis negativ, fällt die Funktion in diesem Intervall.
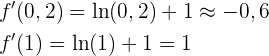
Die Funktion fällt somit im Intervall  und steigt im Intervall
und steigt im Intervall 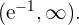
Berechne die Hoch- und Tiefpunkte der Funktionen: 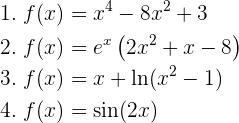
1  Zunächst wird die Ableitung der Funktion berechnet und gleich 0 gesetzt. Wir berechnen die Nullstellen.
Zunächst wird die Ableitung der Funktion berechnet und gleich 0 gesetzt. Wir berechnen die Nullstellen.
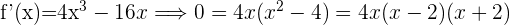
Die Nullstellen sind 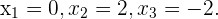 Wir berechnen die 2. Ableitung und setzen die Nullstellen ein:
Wir berechnen die 2. Ableitung und setzen die Nullstellen ein:
Wenn das Ergebnis positiv ist, entsprechen die Koordinaten 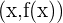 einem Tiefpunkt.
einem Tiefpunkt.
Wenn das Ergebnis negativ ist, entsprechen die Koordinaten 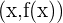 einem Hochpunkt.
einem Hochpunkt.

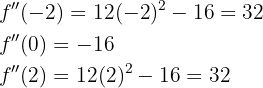
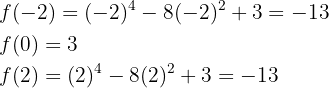
Somit hat die Funktion bei  zwei Tiefpunkte und bei
zwei Tiefpunkte und bei 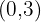 einen Hochpunkt.
einen Hochpunkt.
2 
Wir berechnen die 1. Ableitung, setzen sie gleich 0 und berechnen ihre Nullstellen.
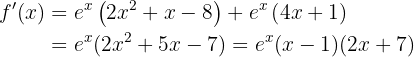
Ihre Nullstellen sind 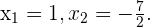 Wir berechnen die 2. Ableitung und setzen die Nullstellen ein:
Wir berechnen die 2. Ableitung und setzen die Nullstellen ein:
Wenn das Ergebnis positiv ist, entsprechen die Koordinaten 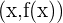 einem Tiefpunkt.
einem Tiefpunkt.
Wenn das Ergebnis negativ ist, entsprechen die Koordinaten 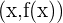 einem Hochpunkt.
einem Hochpunkt.
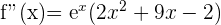
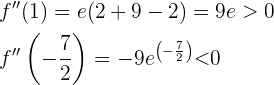
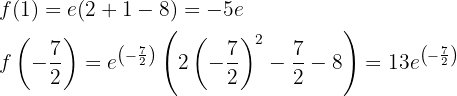
Somit hat die Funktion bei  einen Tiefpunkt und bei
einen Tiefpunkt und bei  einen Hochpunkt.
einen Hochpunkt.
3 
Zunächst berechnen wir den Definitionsbereich, um zu wissen, wo die Funktion definiert ist. Es ist bekannt, dass der Logarithmus nur für positive Zahlen gilt. Also:
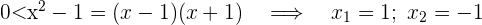
Die ermittelten Punkte teilen die Zahlengerade in 3 Intervalle:  Wir nehmen einen Wert in jedem Intervall und überprüfen, ob die ermittelten Zahlen größer als 0 sind. Der Definitionsbereich ist
Wir nehmen einen Wert in jedem Intervall und überprüfen, ob die ermittelten Zahlen größer als 0 sind. Der Definitionsbereich ist 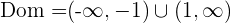 und somit:
und somit:
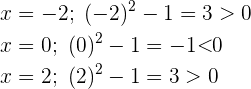
Wir berechnen die 1. Ableitung, setzen sie gleich 0 und berechnen ihre Nullstellen.
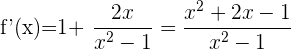
Ihre Nullstellen sind 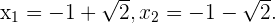 Nur der 2. Wert wird berücksichtigt, da der 1. nicht in den Definitionsbereich der Funktion fällt. Wir berechnen die 2. Ableitung und setzen die Nullstelle ein:
Nur der 2. Wert wird berücksichtigt, da der 1. nicht in den Definitionsbereich der Funktion fällt. Wir berechnen die 2. Ableitung und setzen die Nullstelle ein:
Wenn das Ergebnis positiv ist, entsprechen die Koordinaten 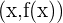 einem Tiefpunkt.
einem Tiefpunkt.
Wenn das Ergebnis negativ ist, entsprechen die Koordinaten 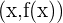 einem Hochpunkt.
einem Hochpunkt.
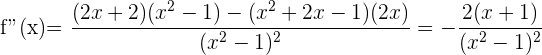
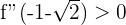
Die Funktion hat also bei 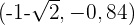 einen Hochpunkt.
einen Hochpunkt.
4 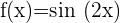
Wir berechnen die 1. Ableitung, setzen sie gleich 0 und berechnen ihre Nullstellen.
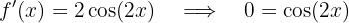
Da die Funktion 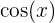 die Periode
die Periode 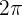 hat, wird sie null für
hat, wird sie null für 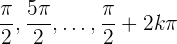 und
und 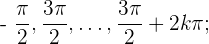 Somit wird die Funktion
Somit wird die Funktion  null für
null für 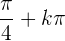 und
und 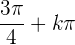
Wir berechnen die 2. Ableitung und werten die Nullstellen aus.
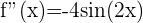
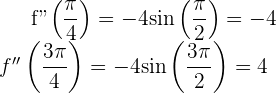
Somit erhalten wir für  Hochpunkte der Form
Hochpunkte der Form 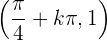 und für
und für 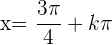 Tiefpunkte der Form
Tiefpunkte der Form 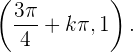
Ermittle die Intervalle der Konkavität und Konvexität sowie die Wendepunkte der Funktionen: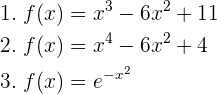
1 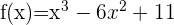 Wir berechnen die 2. Ableitung, setzen sie gleich 0 und berechnen ihre Nullstellen.
Wir berechnen die 2. Ableitung, setzen sie gleich 0 und berechnen ihre Nullstellen.
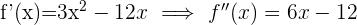
Ihre Nullstelle ist  Wir unterteilen die Zahlengerade in 2 Intervalle:
Wir unterteilen die Zahlengerade in 2 Intervalle: 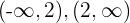 und nehmen einen Punkt in jedem Intervall:
und nehmen einen Punkt in jedem Intervall:
Ist das Ergebnis positiv, ist der Graph konvex.
Ist das Ergebnis negativ, ist der Graph konkav.
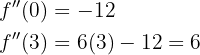
Der Graph ist also konkav bei 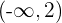 und konvex bei
und konvex bei  .
.
Um die Wendepunkte zu finden, setzen wir die Nullstellen der 2. Ableitung in die 3. Ableitung ein. Erhält man einen Wert ungleich 0, so handelt es sich um einen Wendepunkt.
Da  , ist der Punkt
, ist der Punkt 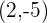 ein Wendepunkt.
ein Wendepunkt.
2 
Wir berechnen die 2. Ableitung, setzen sie gleich 0 und berechnen ihre Nullstellen.
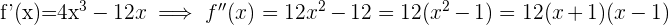
Ihre Nullstellen sind 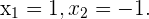 Wir unterteilen die Zahlengerade in 3 Intervalle
Wir unterteilen die Zahlengerade in 3 Intervalle 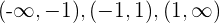 und nehmen einen Punkt in jedem Intervall:
und nehmen einen Punkt in jedem Intervall:
Ist das Ergebnis positiv, ist der Graph konvex.
Ist das Ergebnis negativ, ist der Graph konkav.
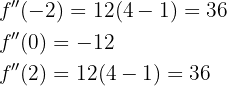
Der Graph ist somit konkav bei  und konvex bei
und konvex bei 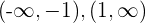 .
.
Um die Wendepunkte zu finden, werden die Nullstellen der 2. Ableitung durch die 3. Ableitung ersetzt. Erhält man einen Wert ungleich 0, so handelt es sich um einen Wendepunkt.
Da 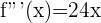 , sind
, sind  Wendepunkte.
Wendepunkte.
3 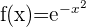
Wir berechnen die 2. Ableitung, setzen sie gleich 0 und berechnen ihre Nullstellen.
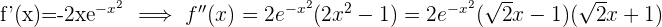
Ihre Nullstellen sind 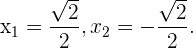 Wir unterteilen die Zahlengerade in 3 Intervalle:
Wir unterteilen die Zahlengerade in 3 Intervalle:  . Wir nehmen einen Punkt in jedem Intervall und kommen zu folgendem Schluss:
. Wir nehmen einen Punkt in jedem Intervall und kommen zu folgendem Schluss:
Wenn das Ergebnis positiv ist, ist der Graph konvex.
Wenn das Ergebnis negativ ist, ist der Graph konkav.
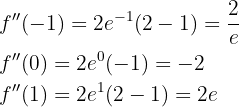
Der Graph ist somit konkav bei 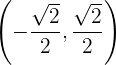 und konvex bei
und konvex bei 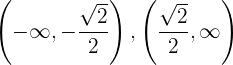 .
.
Um die Wendepunkte zu finden, werden die Nullstellen der 2. Ableitung durch die 3. Ableitung ersetzt. Erhält man einen Wert ungleich 0, so handelt es sich um einen Wendepunkt.
Da 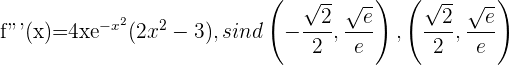 Wendepunkte.
Wendepunkte.
Die Entwicklung des Aktienkurses eines bestimmten Unternehmens ist unter der Annahme, dass die Börse in einem Monat mit 30 Tagen  Tage in Betrieb bleibt, definiert durch:
Tage in Betrieb bleibt, definiert durch:
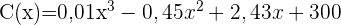
1 1 Berechne die Höchst- und Mindestnotierungen sowie die Tage, an denen sie angefallen sind, an anderen Tagen als dem ersten und letzten Tag.
2 Bestimme die Zeiträume, in denen die Aktien gestiegen oder gefallen sind.
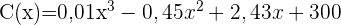
1 Berechne die Höchst- und Mindestnotierungen sowie die Tage, an denen sie angefallen sind, an anderen Tagen als dem ersten und letzten Tag.
Wir leiten die Funktion ab, setzen sie gleich 0 und berechnen ihre Nullstellen.
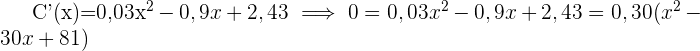
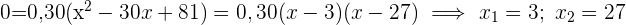
Wir erhalten die 2. Ableitung der Funktion und werten die Nullstellen aus. Somit:
Wenn der Wert positiv ist, haben wir einen Tiefpunkt.
Wenn der Wert negativ ist, haben wir einen Hochpunkt.
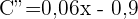
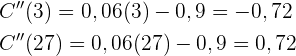
Daher hatte das Unternehmen am 3. Handelstag einen Höchststand von 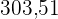 und am 27. Tag einen Tiefststand von
und am 27. Tag einen Tiefststand von 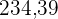 .
.
2 Bestimme die Zeiträume, in denen die Aktien gestiegen oder gefallen sind.
Wir unterteilt die Zahlen von 1 bis 30 in die Intervalle  unter Berücksichtigung der Nullstellen der 1. Ableitung. Dann wird aus jedem Intervall ein Wert entnommen und ausgewertet, um die Intervalle herauszufinden, in denen die Funktion steigt oder fällt:
unter Berücksichtigung der Nullstellen der 1. Ableitung. Dann wird aus jedem Intervall ein Wert entnommen und ausgewertet, um die Intervalle herauszufinden, in denen die Funktion steigt oder fällt:
Ist das Ergebnis positiv, steigt die Funktion in diesem Intervall.
Ist das Ergebnis negativ, fällt die Funktion in diesem Intervall.
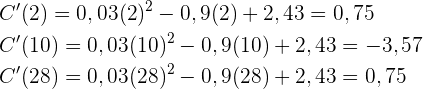
In den ersten 3 Tagen stieg der Börsenkurs an. Dann, bis zum 27. Tag, war der Aktienkurs rückläufig. Nach diesem Tag begann er wieder zu steigen.
Angenommen, die in Prozent gemessene Leistung  eines Schülers in einer einstündigen Prüfung entspricht dem Ausdruck
eines Schülers in einer einstündigen Prüfung entspricht dem Ausdruck
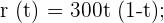 ,
,
wobei 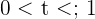 die Zeit in Stunden angibt.
die Zeit in Stunden angibt.
1 An welchen Punkten nimmt die Leistung zu oder ab?
2 Wann ist die Leistung gleich 0?
3 Wann ist die Leistung am höchsten und wie hoch ist sie?

1 An welchen Punkten nimmt die Leistung zu oder ab?
Wir leiten die Funktion ab, setzen sie gleich 0 und berechnen ihre Nullstellen.

Die Nullstelle der 1. Ableitung teilt das Intervall  in die Intervalle
in die Intervalle 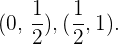 Anschließend nehmen wir einen Wert aus jedem Intervall und setzen ihn in die Ableitung ein, um herauszufinden, in welchen Intervallen die Funktion steigt oder fällt:
Anschließend nehmen wir einen Wert aus jedem Intervall und setzen ihn in die Ableitung ein, um herauszufinden, in welchen Intervallen die Funktion steigt oder fällt:
Ist das Ergebnis positiv, steigt die Funktion in diesem Intervall.
Ist das Ergebnis negativ, fällt die Funktion in diesem Intervall.
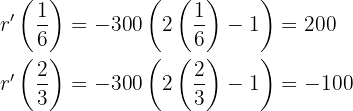
Daher ist die Leistung in der ersten Hälfte der Prüfung höher als in der zweiten Hälfte.
2 Wann ist die Leistung gleich 0?
Wir setzen die Funktion gleich 0 und berechnen ihre Nullstellen.

Somit ist die Leistung zu Beginn und am Ende der Prüfung gleich 0.
3 Wann ist die Leistung am höchsten und wie hoch ist sie?
Wir berechnen die 2. Ableitung und setzen die Nullstelle der 1. Ableitung ein.

Die höchste Leistung wird also nach einer halben Stunde erreicht. Wenn man die Funktion auswertet, beträgt die höchste Leistung 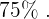
Mit KI zusammenfassen:












