Kapitel

Das Additions-/Subtraktionsverfahren
Mit der Methode des Additions-/Subtraktionsverfahrens addiert oder subtrahiert man  Gleichungen, um eine dritte Gleichung zu erhalten. Diese dritte Gleichung hat eine Variable weniger als die Ausgangsgleichungen, wodurch die anderen Variablen bestimmt werden können.
Gleichungen, um eine dritte Gleichung zu erhalten. Diese dritte Gleichung hat eine Variable weniger als die Ausgangsgleichungen, wodurch die anderen Variablen bestimmt werden können.
Beispiel
Gegeben sind folgende Gleichungssysteme:
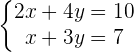
Wir stellen fest, dass es sich um ein System mit zwei Gleichungen mit zwei Unbekannten handelt. Wir gehen also davon aus, dass das System nur eine einzige Lösung hat. Somit:
Schritt 1: Wir überprüfen, ob beide Gleichungen addiert oder subtrahiert werden können und wir somit eine der Variablen kürzen können.
Da wir nicht direkt kürzen können, müssen wir eine der beiden Gleichungen mit irgendeinem Wert multiplizieren, sodass wir in beiden Gleichungen eine Variable haben, deren Koeffizient in beiden Gleichungen übereinstimmt.
Schritt 2: Sobald wir Variablen haben, deren Koeffizienten übereinstimmen, können diese subtrahiert werden und eine der Variablen kann somit weggekürzt werden.
Schritt 3: Wir müssen in der erhaltenen Gleichung die Variable bestimmen.
Schritt 4: Wir setzen die Variable in eine der beiden Gleichungen ein, um den Wert der anderen Variablen zu erhalten.
Wir lösen:

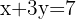
Schritt 1: Da keine der Variablen den gleichen Koeffizienten hat, müssen wir multiplizieren. Die zweite Gleichung muss mit  multipliziert werden:
multipliziert werden:
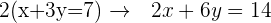
Nun haben wir :
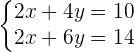
Schritt 2: Da wir bei einer der Variablen gleiche Koeffizienten haben, können wir die Gleichungen subtrahieren:

Schritt 3: Wir bestimmen  .
.
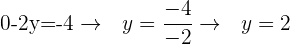
Schritt 4: Wir setzen  in die erste oder zweite Gleichung ein.
in die erste oder zweite Gleichung ein.

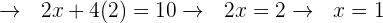
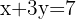

Das System lösen - Ganzzahlige Koeffizienten
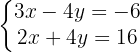
Da die Variable  in beiden Gleichungen den gleichen Koeffizienten hat, aber mit jeweils unterschiedlichem Vorzeichen, können wir die beiden Gleichungen addieren.
in beiden Gleichungen den gleichen Koeffizienten hat, aber mit jeweils unterschiedlichem Vorzeichen, können wir die beiden Gleichungen addieren.

Wir bestimmen die Variable, um ihren Wert herauszufinden:
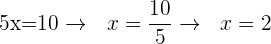
Wir setzen den Wert für  in die zweite Ausgangsgleichung ein.
in die zweite Ausgangsgleichung ein.
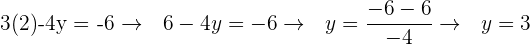
Die Lösung ist :
 y
y 
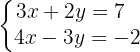
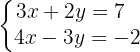
Wir möchten, dass die Variable  wegfällt. Dazu multiplizieren wir die erste Gleichung mit
wegfällt. Dazu multiplizieren wir die erste Gleichung mit  und die zweite mit
und die zweite mit  .
.
Wir addieren Glied für Glied und erhalten den Wert für  .
.
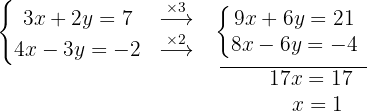
Wir setzen den Wert für  in die erste Ausgangsgleichung ein.
in die erste Ausgangsgleichung ein.
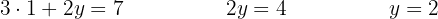
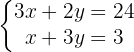
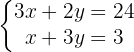
Wir möchten, dass die Variable  wegfällt. Dazu multiplizieren wir die zweite Gleichung mit
wegfällt. Dazu multiplizieren wir die zweite Gleichung mit  .
.
Wir addieren Glied für Glied und erhalten den Wert für  .
.
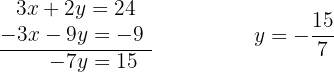
Wir setzen den Wert für  in die zweite Ausgangsgleichung ein.
in die zweite Ausgangsgleichung ein.
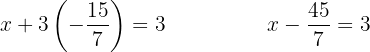
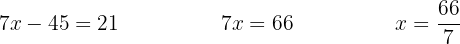
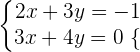
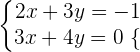
Wir möchten, dass die Variable  wegfällt. Dazu multiplizieren wir die erste Gleichung mit
wegfällt. Dazu multiplizieren wir die erste Gleichung mit  und die zweite mit
und die zweite mit  .
.
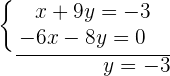
Wir setzen den Wert für  in die zweite Ausgangsgleichung ein.
in die zweite Ausgangsgleichung ein.

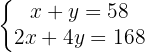
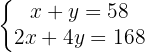
Wir möchten, dass die Variable  wegfällt. Dazu multiplizieren wir die erste Gleichung mit
wegfällt. Dazu multiplizieren wir die erste Gleichung mit 
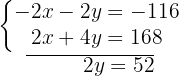
Wir berechnen den Wert für 
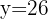
Wir setzen den Wert für  in die erste Gleichung ein.
in die erste Gleichung ein.

Das System lösen - Rationale Koeffizienten
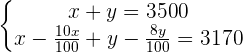
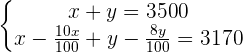
Wir kürzen die Nenner in der zweiten Gleichung, indem wir  mit
mit 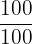 multiplizieren.
multiplizieren.
Dieser Bruch entspricht  . Somit ändert sich die Proportionalität der Gleichung nicht; es handelt sich einfach nur um einen Trick, der die Berechnung einfacher macht.
. Somit ändert sich die Proportionalität der Gleichung nicht; es handelt sich einfach nur um einen Trick, der die Berechnung einfacher macht.
Wir erhalten:
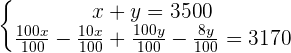
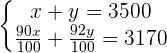
Um die Nenner in der zweiten Gleichung loszuwerden, multiplizieren wir 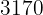 mit
mit  . Das neue System lautet:
. Das neue System lautet:
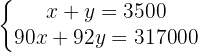
Wir wenden das Additionsverfahren an. Dazu müssen wir eine der Unbekannten loswerden, indem wir die beiden Gleichungen addieren. Wir multiplizieren also die erste Gleichung mit 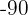 und werden so unser
und werden so unser  los. Indem wir die beiden Gleichungen addieren, erhalten wir eine Gleichung mit einer Unbekannten (
los. Indem wir die beiden Gleichungen addieren, erhalten wir eine Gleichung mit einer Unbekannten ( )/p>
)/p>
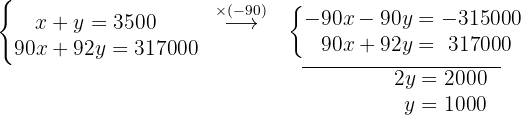
Wir erhalten den Wert für 

Wir setzen den Wert für  in die erste Ausgangsgleichung ein.
in die erste Ausgangsgleichung ein.

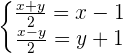
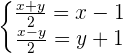
Wir entfernen die Nenner. Dazu multiplizieren wir die Gleichungen mit 2, da in beiden nur dieser Nenner vorkommt:
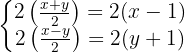
Da auf der linken Seite der Gleichungen mit oder durch die gleiche Zahl multipliziert und dividiert wird, kann 2 weggekürzt werden
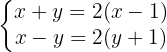
Wir lösen die Klammern auf
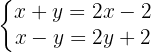
Wir ordnen die Terme, die Variablen auf einer Seite und das konstante Glied auf der anderen Seite
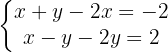
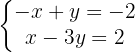
Da in den Gleichungen x und -x vorkommt, können wir direkt vereinfachen (Addition der Gleichungen) und die Variable x entfernen, da -x+x=0. Wir addieren Glied für Glied und berechnen den Wert für  .
.
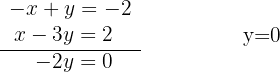
Wir setzen den Wert für  in die zweite Gleichung des Systems ein (man kann auch die erste Gleichung nehmen) und bestimmen
in die zweite Gleichung des Systems ein (man kann auch die erste Gleichung nehmen) und bestimmen
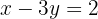


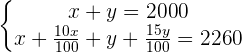
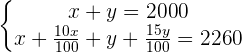
Wir entfernen die Nenner der zweiten Gleichung, indem wir mit 100 multiplizieren.


Wir kürzen 100 aus den Termen, in denen sie als Faktor vorkommt; somit gilt 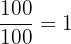
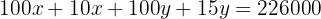
wir addieren ähnliche Terme, um zu vereinfachen
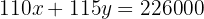
Wir möchten, dass  wegfällt. Dazu multiplizieren wir die erste Gleichung mit
wegfällt. Dazu multiplizieren wir die erste Gleichung mit 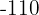
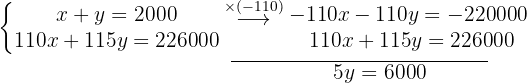
Wir erhalten den Wert für  .
.
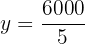

Wir setzen den Wert für  in die erste Gleichung ein und bestimmen.
in die erste Gleichung ein und bestimmen.


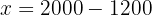
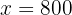
Mit KI zusammenfassen:













