Was untersucht die Kombinatorik?
Die Kombinatorik befasst sich mit Methoden zum Zählen der verschiedenen Konfigurationen von Elementen einer Menge, die bestimmte festgelegte Kriterien erfüllen.
Bei jedem kombinatorischen Problem gibt es mehrere Schlüsselbegriffe, die wir unterscheiden müssen:
1 Grundgesamtheit
Es handelt sich um die Menge der Elemente, die wir untersuchen. Wir bezeichnen die Anzahl der Elemente dieser Menge mit 
.
2 Stichprobe
Es handelt sich um eine Teilmenge der Grundgesamtheit. Die Anzahl der Elemente, aus denen sich die Stichprobe zusammensetzt, bezeichnen wir mit 
.
Die verschiedenen Arten von Stichproben werden durch zwei Aspekte bestimmt:
Reihenfolge
Das heißt, ob es wichtig ist, dass die Elemente der Stichprobe geordnet erscheinen oder nicht.
Wiederholung
Die Möglichkeit der Wiederholung oder Nichtwiederholung der Elemente.
Beispiel:
In einer Tanzklasse gibt es 10 Schüler*innen und man möchte ein Komitee aus 
Personen bilden, das die Aufführungen organisiert. Auf wie viele verschiedene Arten ist dies möglich?
Grundgesamtheit: Die 
Schüler*innen
Stichprobe: Ein mögliches Komittee: Anna, Rosa, Valerie und Carla.
Spielt die Reihenfolge eine Reihe?
In diesem Fall nicht, denn wenn wir die Elemente in unserer Stichprobe anders anordnen, erhalten wir dasselbe Komitee.
Das heißt, Anna, Rosa, Valerie und Carla bilden dasselbe Komitee wie Carla, Rosa, Anna und Valerie.
Können sich Elemente in der Stichprobe wiederholen?
Nein, da es sich um Personen handelt, also um Elemente, die nicht wiederholt werden können, und beispielsweise Anna, Anna, Rosa und Anna nicht als gültiges Komitee angesehen werden.
Später im Studium der Kombinatorik wirst du sehen, dass die Antwort auf diese Frage lautet:
Fakultät einer Zahl
Es ist das Produkt der aufeinanderfolgenden Faktoren von 
bis . Die Fakultät einer natürlichen Zahl wird mit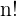 
angegeben.
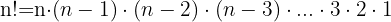
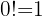
Beispiel:
Berechne die Fakultät 
.
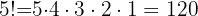
Grundprinzip der Zählung
Wenn eine bestimmte Aufgabe auf verschiedene Arten ausgeführt werden kann und für jede dieser Arten eine zweite Aufgabe auf verschiedene Arten ausgeführt werden kann, dann können die beiden Aufgaben auf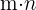 
verschiedene Arten ausgeführt werden.
Beispiele:
- Wenn ich verschiedene T-Shirts und
verschiedene Hosen habe, wie viele verschiedene Outfits kann ich dann zusammenstellen?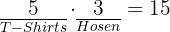
- Wie viele natürliche Zahlen mit oder weniger Ziffern gibt es?
- Die Antwort ist einfach: Es gibt
Zahlen, also alle ganzen Zahlen von 
bis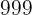 
.
Wir können es jedoch wie folgt betrachten:
Es gibt höchstens einstellige Zahlen: 
und 
. Um die Zahlen bis zu zwei Ziffern ( bis 
) zu zählen, müssen nicht alle geschrieben werden. Es reicht aus, zu beachten, dass die erste Ziffer eine beliebige der Ziffern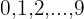 
sein kann und dass es für jede dieser Ziffern 10 verschiedene Endungen gibt; beispielsweise sind die Zahlen, die mit beginnen: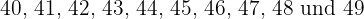 
, 10 insgesamt. Somit beträgt die Anzahl der ganzen Zahlen mit höchstens zwei Ziffern: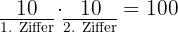 
Das Zählen von Zahlen mit maximal 3 Ziffern erfolgt auf ähnliche Weise:
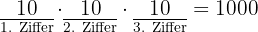
Mit KI zusammenfassen:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
