Kapitel
Permutationen
Auf wie viele verschiedene Arten können acht Personen in einer Sitzreihe sitzen?
Alle Elemente sind enthalten. In der Sitzreihe können sich 
Personen hinsetzen.
Die Reihenfolge spielte eine Rolle. Wenn die Personen anders angeordnet werden, zählt dies als eine andere Art.
Die Elemente wiederholen sich nicht. Eine Person kommt nur einmal vor.
Aufgrund der Merkmale handelt sich um eine Permutation.
Wie viele Zahlen können mit 
unterschiedlichen der folgenden Zahlen gebildet werden: 
?
In der Angabe steht, dass es sich um unterschiedliche Zahlen handeln muss.
Nicht alle Elemente sind enthalten. Von 
sind nur enthalten
Die Reihenfolge spielt eine Rolle. 
sind unterschiedliche Zahlen.
Die Elemente wiederholen sich nicht. Laut Angabe muss es sich um unterschiedliche Zahlen handeln
Aufgrund der Merkmale handelt es sich um eine Variation
Auf wie viele verschiedene Arten können acht Personen an einem runden Tisch angeordnet werden?
In diesem Fall wollen wir berechnen, wie viele Möglichkeiten es gibt, Personen im Kreis anzuordnen. Deshalb greifen wir auf kreisförmige Permutationen zurück.
Wie viele Fußballtippscheine müssen ausgefüllt werden, um sicherzustellen, dass alle 
Ergebnisse richtig sind?
Bei jedem der Spiele kann auf einen Sieg, ein Unentschieden oder eine Niederlage der Heimmannschaft gesetzt werden:
m < n
Alle Elemente sind enthalten. In diesem Fall ist die Anzahl der Spiele größer als die Anzahl der Elemente.
Die Reihenfolge spielt eine Rolle.
Die Elemente wiederholen sich.
Aufgrund der Merkmale handelt es sich um eine Variation
Gegeben sind die Zahlen 
und . Wie viele 5-stellige Zahlen können gebildet werden? Wie viele davon sind gerade Zahlen?
1 5-stellige Zahlen. Alle Elemente sind enthalten: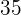 
Die Reihenfolge spielt eine Rolle
Die Elemente wiederholen sich
Aufgrund der Merkmale handelt es sich um eine Variation mit Wiederholung
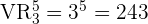
2 -stellige, gerade Zahlen
Wenn eine Zahl gerade ist, kann sie nur auf 
enden.
Gegeben sind die Zahlen 
. Wie viele neue Zahlen können mit diesen Zahlen gebildet werden?
Alle Elemente sind enthalten
Die Reihenfolge spielt eine Rolle
Die Elemente wiederholen sich
Aufgrund der Merkmale handelt es sich um eine Permutation mit Wiederholung
Gegeben ist das Wort Apfel. Wie viele Anordnungen gibt es, die mit einem Vokal beginnen?
Das Wort beginnt also mit a oder e, gefolgt von den restlichen 
Buchstaben aus in .
Alle Elemente sind enthalten
Die Reihenfolge spielt eine Rolle
Die Elemente wiederholen sich nicht
Aufgrund der Merkmale handelt es sich um Permutationen
Für den ersten Buchstaben gibt es 
Möglichkeiten und für den Rest gibt es 
Möglichkeiten. Es müssen also die Buchstaben p, f, l und der Buchstabe, der nicht am Anfang steht, angeordnet werden. Daraus ergibt sich
Wie viele verschiedene 5-stellige Zahlen können mit den ungeraden Zahlen gebildet werden? Wie viele von ihnen sind größer als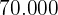 
?
1 Zahlen mit fünf unterschiedlichen Ziffern
Die ungeraden Zahlen:
Alle Elemente sind enthalten
Die Reihenfolge spielt eine Rolle
Die Elemente wiederholen sich nicht
Aufgrund der Merkmale handelt es sich um eine Permutation
2 Größer als 
Wenn eine Zahl ungerade ist, kann sie nur mit 7 oder 8 beginnen
An einem Schiffssignalmast können drei rote, zwei blaue und vier grüne Flaggen gehisst werden. Wie viele verschiedene Signale können durch die Platzierung der neun Flaggen angezeigt werden?
Alle Elemente sind enthalten.
Die Reihenfolge spielt eine Rolle
Die Elemente wiederholen sich
Aufgrund der Merkmale handelt es sich um eine Permutation mit Wiederholung
Ein Gremiumstisch besteht aus acht Personen. Wie viele verschiedene Sitzmöglichkeiten gibt es, wenn der Vorsitzende und der Sekretär immer zusammen sitzen?
Zunächst müssem wir überlegen, wie viele Möglichkeiten es gibt, den Platz für den Vorsitzenden und den Sekretär unterzubringen. Dieser Platz für zwei Personen kann vom ersten, zweiten, dritten bis zum siebten Platz reichen, wobei der Vorsitzende und der Sekretär die beiden letzten Plätze einnehmen. Insgesamt stehen für diesen Platz 
Möglichkeiten zur Auswahl.Es werden zwei Gruppen gebildet, von denen die erste Gruppe aus Personen (Vorsitzender und Sekretär) und die zweite Gruppe aus 
Personen besteht. Für beide Gruppen gilt Folgendes:
Alle Elemente sind enthalten
Die Reihenfolge spielt eine Rolle
Die Elemente wiederholen sich nicht
Aufgrund der Merkmale handelt es sich um Permutationen.
In einer Reihe befinden sich rote Kugeln, weiße Kugeln und blaue Kugeln. Wenn die Kugeln der gleichen Farbe nicht voneinander zu unterscheiden sind, auf wie viele Arten können sie angeordnet werden?
Alle Elemente sind enthalten
Die Reihenfolge spielt eine Rolle
Die Elemente wiederholen sich
Aufgrund der Merkmale handelt es sich um eine Permutation mit Wiederholung.
Vier verschiedene Mathematikbücher, sechs verschiedene Physikbücher und zwei verschiedene Chemiebücher stehen in einem Regal. Auf wie viele verschiedene Arten können sie angeordnet werden, wenn:
1Die Bücher für jedes Fach müssen zusammen aufbewahrt werden.
2Nur die Mathebücher müssen zusammen aufbewahrt werden.
1 Die Bücher für jedes Fach müssen zusammen aufbewahrt werden.
Nach Fach geordnet
Zunächst müssen wir die Reihenfolge der Fächer festlegen. Zum Beispiel: zuerst die Mathebücher, dann die Chemiebücher und schließlich die Physikbücher. Es gibt 3 Fächer, wobei
Alle Elemente sind enthalten
Die Reihenfolge spielt eine Rolle
Die Elemente wiederholen sich nicht
Aufgrund der Merkmale handelt es sich um eine Permutation.
Es gibt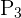 
Möglichkeiten zur Anordnung der Fächer.
Möchtes du dein Mathewissen mit Mathenachhilfe auffrischen?
Reihenfolge der Bücher nach Abschnitten
Nachdem wir uns für diese Anordnung entschieden haben, überlegen wir, wie wir die Bücher für jedes Fach an dem dafür vorgesehenen Platz anordnen können.
Wir beachten:
Alle Elemente sind enthalten
Die Reihenfolge spielt eine Rolle
Die Elemente wiederholen sich nicht
Aufgrund der Merkmale handelt es sich um Permutationen.
Es gibt Möglicheiten, die Mathematikbücher an ihrem Platz anzuordnen, 
Möglichkeiten für die Physikbücher und Möglichkeiten für die Chemiebücher.
Und somit:
2 Nur die Mathematikbücher stehen zusammen.
Anordnung des mathematischen Teils
Zuerst müssen wir überlegen, wie viele Möglichkeiten es gibt, die 4 Mathematikbücher im Regal unterzubringen.
Der Platz für die Mathematikbücher kann mit dem ersten Platz beginnen, mit dem zweiten, dritten, ... bis zum neunten Platz, so dass die Mathematikbücher am Ende stehen würden:
Insgesamt gibt es also 
Möglichkeiten, die Position des Mathebuchteils zu wählen.
Anordnung der Bücher im zugewiesenen Raum
Sobald der Bereich ausgewählt ist, gibt es Möglichkeiten, die Mathematikbücher in diesem Bereich anzuordnen.
Es sind noch 8 Plätze frei, um die restlichen Bücher ohne Einschränkung unterzubringen, wobei
Alle Elemente sind enthalten
Die Reihenfolge spielt eine Rolle
Die Elemente wiederholen sich nicht
Aufgrund der Merkmale handelt es sich um eine Permutation. Es gibt 
Möglichkeiten, die restlichen Bücher anzuordnen.
Insgesamt gibt es folgende Möglichkeiten, die Bücher in dem Regal anzuordnen, in dem die Mathematikbücher zusammen stehen:
Variationen
Wie viele 3-stellige Zahlen lassen sich mit den Ziffern bilden: 
?
1 Erste Zahl
Wir müssen die Zahl in zwei Blöcke aufteilen
Der erste Block einer Zahl kann nur mit einer von Ziffern belegt werden, da eine Zahl nicht mit Null beginnt (außer bei Nummernschildern, Lottozahlen und anderen Sonderfällen)
2 Zweite und dritte Zahl
Der zweite Block, der aus zwei Zahlen besteht, kann mit einer beliebigen Ziffer belegt werden.
In beiden Fällen:
Alle Elemente sind enthalten.
Die Reihenfolge spielt eine Rolle.
Die Elemente wiederholen sich.
Aufgrund der Merkmale handelt es sich um Variationen
Die Möglichkeiten, den ersten Block zu füllen, multipliziert mit den Möglichkeiten, den zweiten zu wählen, ergibt die Gesamtzahl von Ziffern
Wie viele verschiedene Signale können mit dem Morse-System (Punkt, Strich) mit maximal vier Tastenanschlägen gesendet werden?
Mit maximal Anschlägen sind Fälle zu berücksichtigen: Signale mit 
, , oder Anschlägen.Bei den Signalen mit Anschlag sind nicht alle Elemente enthalten, bei den anderen schon
Die Reihenfolge spielt eine Rolle
Die Elemente wiederholen sich
Aufgrund der Merkmale handelt es sich um eine Variation mit Wiederholung
Auf wie viele verschiedene Arten können die Posten des Präsidenten, des Vizepräsidenten und des Schatzmeisters eines Fußballvereins besetzt werden, wenn man weiß, dass es 
mögliche Kandidaten gibt?
Nicht alle Elemente sind enthalten
Die Reihenfolge spielt eine Rolle
Die Elemente wiederholen sich nicht
Aufgrund der Merkmale handelt es sich um eine Variation.
Bestimme die Anzahl der 8-stelligen symmetrischen Zahlen. Wie viele 9-stellige symmetrische Zahlen gibt es?
Symmetrische Zahlen werden von rechts nach links und links nach rechts gleich gelesen.
1 -stellige symmetrische Zahlen
Da die Zahlen ab der fünften in Funktion der ersten Zahlen erscheinen, fällt die Anzahl der 8-stelligen symmetrischen Zahlen mit den -stelligen Zahlen zusammen. Wir müssen uns nun ansehen, auf wie viele Arten wir die Werte für a, b, c und d wählen können, wobei 
.
Hierzu ermitteln wir die Zahlen mit Ziffern und subrahieren diejenigen, die mit 
beginnen.
Nicht alle Elemente sind enthalten. Wir haben 
Ziffern als Elemente und möchten Plätze zuordnen.
Die Reihenfolge spielt eine Rolle
Die Elemente wiederholen sich
Aufgrund der Merkmale handelt es sich um eine Variation mit Wiederholung.
2 -stellige symmetrische Zahlen
Analog zum vorhergehenden Fall gilt:
Wir sehen uns die -stelligen Zahlen an.
Wir subtrahieren die Zahlen, die mit beginnen.
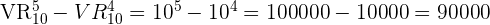
Kombinationen
Wie viele Möglichkeiten gibt es, die sieben Farben des Regenbogens zu mischen, wenn man jeweils drei Farben nimmt?
Nicht alle Elemente sind enthalten. Insgesamt gibt es Farben, von denen Gruppen aus Farben berücksichtigt werden.
Die Reihenfolge spielt keine Rolle. Die Farben werden gemischt, d. h. Rot, Blau und Gelb ergeben die gleiche Farbe wie Gelb, Blau und Rot.
Die Elemente wiederholen sich nicht. Der Regenbogen besteht aus verschiedenen Farben, von denen ausgewählt werden.
Aufgrund der Merkmale handelt es sich um eine Kombination
In einer Klasse sind 
Schüler. Drei Schüler sollen eine Arbeitsgruppe bilden. Wie viele verschiedene Arbeitsgruppen können gebildet werden?
Nicht alle Elemente sind enthalten. Das Komitee besteht nur aus Personen.
Die Reihenfolge spielt keine Rolle: Johann, Anna und Betti bilden genauso eine Gruppe wie Betti, Johann und Anna.
Die Elemente wiederholen sich nicht. Eine Person kann nur einmal vorkommen.
Aufgrund der Merkmale handelt es sich um eine Kombination
Wie viele einspaltige Lottoscheine müssen ausgefüllt werden, um sicherzustellen, dass alle sechs Ergebnisse von 
richtig sind?
Bei der Lotterie müssen Zahlen aus Zahlen ausgewählt werden. Schließlich werden Zahlen nach dem Zufallsprinzip gezogen. Wenn ein Lottospieler diese Zahlen tippt, gewinnt er.Nicht alle Elemente sind enthalten. Nur Elemente aus sind richtig.
Die Reihenfolge spielt keine Rolle.
Die Elemente wiederholen sich nicht.
Aufgrund der Merkmale handelt es sich um eine Kombination
Bei der Lotterie müssen Zahlen aus Zahlen ausgewählt werden. Schließlich werden Zahlen nach dem Zufallsprinzip gezogen. Wenn ein Lottospieler diese Zahlen tippt, gewinnt er.
Nicht alle Elemente sind enthalten. Nur Elemente aus sind richtig.
Die Reihenfolge spielt keine Rolle.
Die Elemente wiederholen sich nicht.
Aufgrund der Merkmale handelt es sich um eine Kombination
Nicht alle Elemente sind enthalten, sondern nur 4.
Die Reihenfolge spielt keine Rolle. Es ist egal, ob Flaschen Rotwein und Flaschen Weißwein oder Flaschen Weißwein und Flaschen Rotwein ausgewählt werden
Die Elemente wiederholen sich. Es kann mehr als eine Flasche vom selben Typ ausgewählt werden
Aufgrund der Merkmale handelt es sich um eine Kombination mit Wiederholung
Wie viele Diagonalen hat ein Fünfeck und wie viele Dreiecke können mit seinen Eckpunkten gebildet werden?
Wir bestimmen die Geraden, die mit Eckpunkten der verfügbaren Eckpunkte (und Dreiecke mit Eckpunkten) gezeichnet werden können.
Nicht alle Elemente sind enthalten
Die Reihenfolge spielt keine Rolle
Die Elemente wiederholen sich nicht
Aufgrund der Merkmale handelt es sich um Kombinationen
Es sind 
. Davon müssen wir die Seiten abziehen, die Geraden bilden, die keine Diagonalen sind.
Diagonalen
Dreiecke
Eine Gruppe besteht aus fünf Männern und sieben Frauen. Nun soll ein Komitee aus Männern und Frauen gebildet werden. Wie viele Möglichkeiten gibt es, dieses Komitee zu bilden, wenn:
1Jeder Mann und jede Frau kann ein Teil des Komitees sein.
2Eine bestimmte Frau muss zum Komitee gehören.
3Zwei bestimmmte Männer dürfen nicht im Komitee sein.
Nicht alle Elemente sind enthalten
Die Reihenfolge spielt keine Rolle
Die Elemente wiederholen sich nicht
Aufgrund der Merkmale handelt es sich hierbei um Kombinationen
1 Jeder Mann und jede Frau kann ein Teil des Komitees sein.
2 Eine bestimmte Frau muss zum Komitee gehören.
3 Zwei bestimmmte Männer dürfen nicht im Komitee sein.
Mit neun Schülern in einer Klasse sollen drei Teams mit je drei Schülern gebildet werden. Wie viele Möglichkeiten gibt es dafür?
Um dieses Problem zu lösen, sehen wir uns an, wie viele Möglichkeiten es gibt, das erste Team zu bilden. Wir multiplizieren dann mit den Möglichkeiten für das zweite Team und den Möglichkeiten für das dritte Team.Nicht alle Elemente sind enthalten. Es werden also Personen aus den verfügbaren Personen ausgewählt.
Die Reihenfolge spielt keine Rolle.
Die Elemente wiederholen sich nicht
Aufgrund der Merkmale handelt es sich um eine Kombination.
Eine Person hat fünf Münzen mit unterschiedlichem Wert. Wie viele verschiedene Summen können mit den fünf Münzen erzielt werden?
Wir betrachten die Summen, die aus Münze, Münzen, Münzen, Münzen oder Münzen bestehen.Nicht alle Elemente sind enthalten (Sie sind alle enthalten, wenn Münzen zum Einsatz kommen)
Die Reihenfolge spielt keine Rolle
Die Elemente wiederholen sich nicht
Aufgrund der Merkmale handelt es sich um Kombinationen.
Falls du immer noch Fragen zu bestimmten Themengebieten in Mathe hast, kannst du dich an einen Superprof-Profi wenden - egal, ob online oder persönlich in deiner Nähe
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
