Wenn eine Funktion an einem Punkt 
ableitbar ist, dann ist sie an stetig.
Das Gegenteil davon ist falsch, d. h. es gibt Funktionen, die an einem Punkt stetig sind, aber dennoch nicht abgeleitet werden können. Im Folgenden sehen wir einige Beispiele, anhand derer wir diese Aussagen untersuchen können.
Beispiele
Untersuche die Stetigkeit und Ableitbarkeit der Funktionen:
1 Wir nehmen
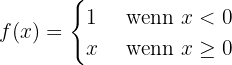
Zunächst untersuchen wir die Stetigkeit bei 
. Wir stellen fest, dass
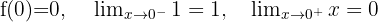
somit ist die Funktion nicht stetig bei und kann somit auch nicht abgeleitet werden.
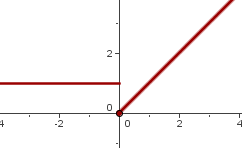
2 Wir nehmen
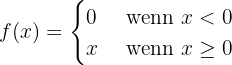
Zunächst untersuchen wir die Stetigkeit bei :
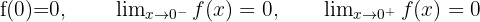
Die Funktion ist stetig, weshalb wir untersuchen können, ob sie abgeleitet werden kann
Da die seitlichen Ableitungen nicht übereinstimmen, ist sie bei nicht ableitbar.
3 Wir nehmen 
:
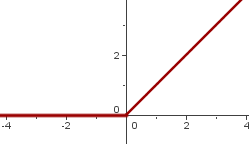
Die Funktion ist stetig bei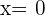 
, weshalb wir untersuchen können, ob sie abgeleitet werden kann.
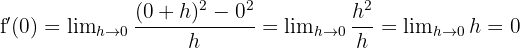
Das heißt, die Funktion ist bei 
stetig und ableitbar.
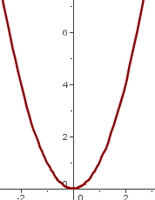
4 Untersuche, für welche Werte von 
und 
die Funktion stetig und ableitbar ist:
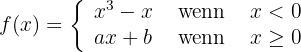
Wir stellen fest, dass
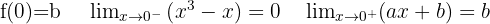
Das heißt, damit sie stetig bei ist, muss 
gelten.
Betrachten wir nun und sehen wir uns an, welchen Wert annehmen muss, damit sie ableitbar ist.
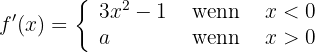
Wir haben
Sie muss also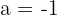 
annehmen.
5 Ermittle die Werte von und , so dass die folgende Funktion in all ihren Punkten abgeleitet werden kann:
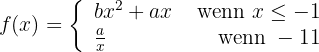
Damit eine Funktion ableitbar ist, muss sie stetig sein. In diesem Fall ist die Funktion für nicht stetig, egal, was und sind. Das heißt, es gibt keine Werte von es decir, no existen valores de und , für die die Funktion stetig wird. Daher gibt es keine Werte und , für die die Funktion ableitbar ist.
6 Untersuche, für welche Werte von und die Funktion stetig und ableitbar ist:
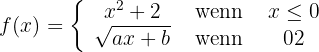
Wir stellen fest, dass
Damit sie bei stetig ist, muss gelten, dass
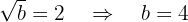
Andererseits für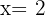 
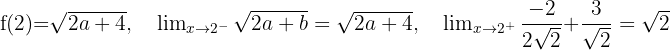
damit sie also stetig bei 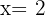ist, muss gelten, dass
Somit ist die Funktion für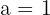 
und 
im gesamten Bereich 
stetig.
Nun haben wir
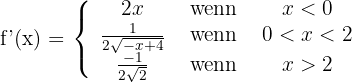
Wir stellen fest, dass
Somit ist sie bei nicht ableitbar und
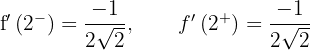
Das heißt, sie ist ableitbar bei 
.
7 Untersuche die Stetigkeit und Ableitbarkeit der wie folgt definierten Funktion
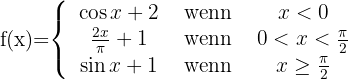
Die Funktion ist nicht stetig bei , da sie keine Abbildung hat. Somit ist sie an diesem Punkt auch nicht ableitbar.
Und nun bei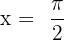 
:
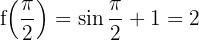
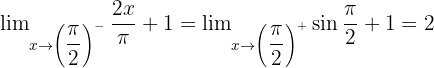
Da sie stetig ist, wollen wir sehen, ob sie sich durch die Formeln der unmittelbaren trigonometrischen Ableitungen ableiten lässt
und stellen fest, dass
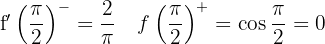
Da die seitlichen Ableitungen nicht übereinstimmen, ist sie an diesem Punkt nicht ableitbar.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
