Berechne die Punkte, an denen die Tangente an den Graphen 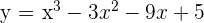 parallel zur x-Achse ist.
parallel zur x-Achse ist.
Berechne die Punkte, an denen die Tangente an den Graphen 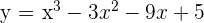 parallel zur x-Achse ist.
parallel zur x-Achse ist.
Die x-Achse hat die Gleichung  , weshalb
, weshalb 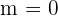
Wir setzen die 1. Ableitung gleich  , um die Berührungspunkte zu ermitteln.
, um die Berührungspunkte zu ermitteln.
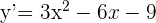 ;
;  (wir vereinfachen durch
(wir vereinfachen durch  )
)
Wir ermitteln die zweiten Koordinaten durch Einsetzen in die Funktion
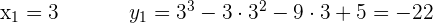


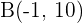
An den Graphen 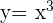 wurde eine Tangente gezeichnet, deren Steigung
wurde eine Tangente gezeichnet, deren Steigung  ist und die durch den Punkt
ist und die durch den Punkt  verläuft. Finde den Berührungspunkt.
verläuft. Finde den Berührungspunkt.
An den Graphen 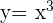 wurde eine Tangente gezeichnet, deren Steigung
wurde eine Tangente gezeichnet, deren Steigung  ist und die durch den Punkt
ist und die durch den Punkt  verläuft. Finde den Berührungspunkt.
verläuft. Finde den Berührungspunkt.
Der Berührungspunkt sei 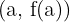

Wir setzen die 1. Ableitung mit der Steigung gleich

Die Gleichungen der Tangenten sind:

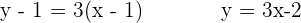


Der Punkt  gehört zur Geraden
gehört zur Geraden  .
.
Somit ist der Berührungspunkt 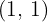 .
.
Finde die Punkte des Graphen  , für die die Tangente einen Winkel von
, für die die Tangente einen Winkel von  mit der x-Achse bildet.
mit der x-Achse bildet.
Finde die Punkte des Graphen  , für die die Tangente einen Winkel von
, für die die Tangente einen Winkel von  mit der x-Achse bildet.
mit der x-Achse bildet.
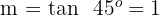
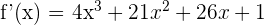
Wir setzen die 1. Ableitung mit der Steigung gleich und lösen die Gleichung
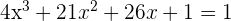
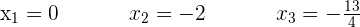
Die 2. Koordinaten erhalten wir durch Einsetzen in die Funktion
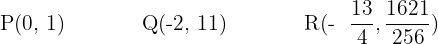
Gegeben ist die Funktion 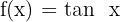 . Finde den Winkel, den die Tangente an den Graphen der Funktion
. Finde den Winkel, den die Tangente an den Graphen der Funktion  im Ursprung mit der x-Achse bildet.
im Ursprung mit der x-Achse bildet.
Gegeben ist die Funktion 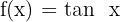 . Finde den Winkel, den die Tangente an den Graphen der Funktion
. Finde den Winkel, den die Tangente an den Graphen der Funktion  im Ursprung mit der x-Achse bildet.
im Ursprung mit der x-Achse bildet.


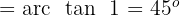
Berechne die Gleichung der Tangente und der Normalen des Graphen 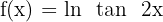 im Punkt der Abszisse:
im Punkt der Abszisse: 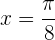 .
.
Berechne die Gleichung der Tangente und der Normalen des Graphen 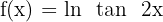 im Punkt der Abszisse:
im Punkt der Abszisse: 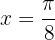 .
.
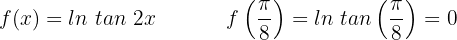
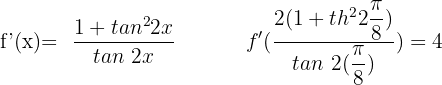
Tangentengleichung:

Normalengleichung:
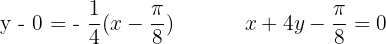
Ermittle die Koeffizienten der Gleichung  , wenn du weißt, dass ihr Graph durch
, wenn du weißt, dass ihr Graph durch  und
und  verläuft und in diesem letzten Punkt die Tangente die Steigung
verläuft und in diesem letzten Punkt die Tangente die Steigung  hat.
hat.
Ermittle die Koeffizienten der Gleichung  , wenn du weißt, dass ihr Graph durch
, wenn du weißt, dass ihr Graph durch  und
und  verläuft und in diesem letzten Punkt die Tangente die Steigung
verläuft und in diesem letzten Punkt die Tangente die Steigung  hat.
hat.
Verläuft durch 
Verläuft durch 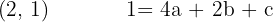

Wir lösen das System und erhalten:
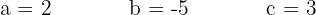
Der Graph der Funktion  verläuft durch die Punkte
verläuft durch die Punkte  und
und 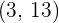 . Die Tangente im Punkt
. Die Tangente im Punkt  auf der x-Achse ist parallel zur Winkelhalbierenden des 1. Quadranten. Berechne den numerischen Wert von
auf der x-Achse ist parallel zur Winkelhalbierenden des 1. Quadranten. Berechne den numerischen Wert von  und
und  .
.
Der Graph der Funktion  verläuft durch die Punkte
verläuft durch die Punkte  und
und 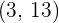 . Die Tangente im Punkt
. Die Tangente im Punkt  auf der x-Achse ist parallel zur Winkelhalbierenden des 1. Quadranten. Berechne den numerischen Wert von
auf der x-Achse ist parallel zur Winkelhalbierenden des 1. Quadranten. Berechne den numerischen Wert von  und
und  .
.
Verläuft durch 
Verläuft durch 

Wir lösen das System und erhalten
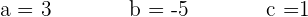
Gegeben ist die Funktion 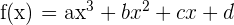 . Berechne
. Berechne  und
und  ; ihr Graph verläuft durch die Punkte
; ihr Graph verläuft durch die Punkte 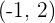 und
und  . Die Tangenten an den Abszissenpunkten
. Die Tangenten an den Abszissenpunkten  und
und  sind parallel zur x-Achse.
sind parallel zur x-Achse.
Gegeben ist die Funktion 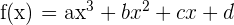 . Berechne
. Berechne  und
und  ; ihr Graph verläuft durch die Punkte
; ihr Graph verläuft durch die Punkte 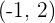 und
und  . Die Tangenten an den Abszissenpunkten
. Die Tangenten an den Abszissenpunkten  und
und  sind parallel zur x-Achse.
sind parallel zur x-Achse.
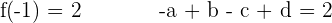
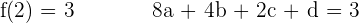
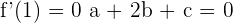
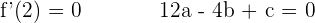
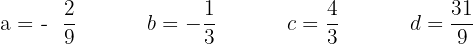
In welchem Punkt des Graphen  verläuft die Tangente parallel zur Sehne, die die Punkte
verläuft die Tangente parallel zur Sehne, die die Punkte  und
und 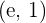 verbindet?
verbindet?
In welchem Punkt des Graphen  verläuft die Tangente parallel zur Sehne, die die Punkte
verläuft die Tangente parallel zur Sehne, die die Punkte  und
und 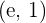 verbindet?
verbindet?
Die Steigung der Sehne muss gleich der Ableitung der Funktion sein.
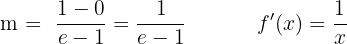

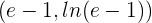
Die Gleichung für eine Kreisbewegung lautet: 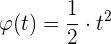 . Wie hoch sind die Geschwindigkeit und die Beschleunigung nach sieben Sekunden?
. Wie hoch sind die Geschwindigkeit und die Beschleunigung nach sieben Sekunden?
Die Gleichung für eine Kreisbewegung lautet: 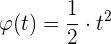 . Wie hoch sind die Geschwindigkeit und die Beschleunigung nach sieben Sekunden?
. Wie hoch sind die Geschwindigkeit und die Beschleunigung nach sieben Sekunden?
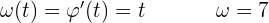
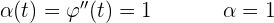
Ein Beobachter befindet sich  vom Startturm einer Rakete entfernt. Wenn sie senkrecht abhebt, misst sie die Veränderung des Winkels
vom Startturm einer Rakete entfernt. Wenn sie senkrecht abhebt, misst sie die Veränderung des Winkels  zwischen der Sichtlinie zur Rakete und dem horizontalen Bodenwinkel in Abhängigkeit von der verstrichenen Zeit. Wir wissen, dass
zwischen der Sichtlinie zur Rakete und dem horizontalen Bodenwinkel in Abhängigkeit von der verstrichenen Zeit. Wir wissen, dass 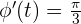 . Berechne:
. Berechne:
- Auf welcher Höhe befindet sich die Rakete, wenn
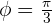 ?
? - Wie schnell ist die Rakete, wenn
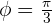 ?
?
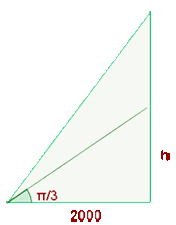
Ein Beobachter befindet sich  vom Startturm einer Rakete entfernt. Wenn sie senkrecht abhebt, misst sie die Veränderung des Winkels
vom Startturm einer Rakete entfernt. Wenn sie senkrecht abhebt, misst sie die Veränderung des Winkels  zwischen der Sichtlinie zur Rakete und dem horizontalen Bodenwinkel in Abhängigkeit von der verstrichenen Zeit. Wir wissen, dass
zwischen der Sichtlinie zur Rakete und dem horizontalen Bodenwinkel in Abhängigkeit von der verstrichenen Zeit. Wir wissen, dass 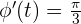 . Berechne:
. Berechne:
a Auf welcher Höhe befindet sich die Rakete, wenn 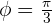 ?
?
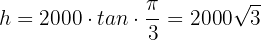
b Wie schnell ist die Rakete, wenn 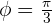 ?
?

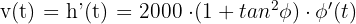
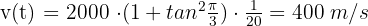
In einen kugelförmigen Ballon wird Gas mit einer Geschwindigkeit von 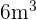 /min gepumpt. Wie schnell ändert sich der Radius des Ballons bei konstantem Druck, wenn der Durchmesser
/min gepumpt. Wie schnell ändert sich der Radius des Ballons bei konstantem Druck, wenn der Durchmesser 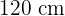 beträgt?
beträgt?
In einen kugelförmigen Ballon wird Gas mit einer Geschwindigkeit von 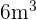 /min gepumpt. Wie schnell ändert sich der Radius des Ballons bei konstantem Druck, wenn der Durchmesser
/min gepumpt. Wie schnell ändert sich der Radius des Ballons bei konstantem Druck, wenn der Durchmesser 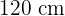 beträgt?
beträgt?
Um dieses Problem zu lösen, benötigen wir die Formel für das Volumen in Abhängigkeit vom Radius:
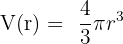
Außerdem wissen wir, dass die Änderungsrate des Volumens 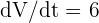 mit der Einheit
mit der Einheit  angegeben.
angegeben.
Um die Funktionen miteinander in Beziehung zu setzen, müssen wir das Volumen in Abhängigkeit von der Zeit schreiben. Wir tun dies, indem wir 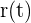 schreiben, da der Radius ebenfalls mit der Zeit variiert. Somit:
schreiben, da der Radius ebenfalls mit der Zeit variiert. Somit:

Nun leiten wir das Volumen in Abhängigkeit von der Zeit ab (wir verwenden die Kettenregel):
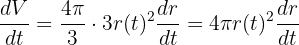
Wir stellen fest, dass wir in der obigen Gleichung bereits alles haben, was wir brauchen. Wir kennen bereits 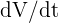 , das konstant ist. Außerdem ist
, das konstant ist. Außerdem ist  die Variable, nach der wir suchen. Wir bestimmen zunächst
die Variable, nach der wir suchen. Wir bestimmen zunächst  .
.
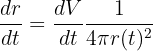
Wir kennen die Zeit nicht, aber wir wissen, dass der Durchmesser 120 cm beträgt, d.h. der Radius ist 60 cm oder 0,6 m. Wir setzen diese Werte ein:
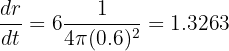
Die Antwort lautet also 1,33 m/min.
Finde den Schnittwinkel zwischen den Graphen 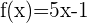 und
und 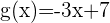
Finde den Schnittwinkel zwischen den Graphen 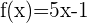 und
und 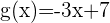
1 Wir wenden die Formel an

2 Wir setzen die beiden Graphen gleich
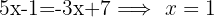
3 Wir berechnen die Steigungen
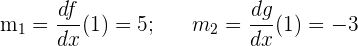
4 Wir setzen in die Formel für den Winkel zwischen zwei Graphen ein
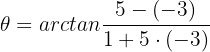
Mit KI zusammenfassen:


