Kapitel
- Ableitungen von trigonometrischen Funktionen
- Ableitungen von trigonometrischen Umkehrfunktionen
- Ableitungen von zusammengesetzten Logarithmusfunktionen und trigonometrischen Funktionen
- Ableitungen von zusammengesetzten Exponentialfunktionen und trigonometrischen Funktionen
- Höhere Ableitungen
- Implizite Ableitung
- Zusätzliche Problemstellungen zur Ableitung

Ableitungen von trigonometrischen Funktionen
Wir werden uns Übungen zur Ableitung trigonometrischer Funktionen ansehen und versuchen, das Verfahren so detailliert wie möglich zu beschreiben. Es wird vorausgesetzt, dass die Ableitungen der trigonometrischen Grundfunktionen bereits bekannt sind.
Leite folgende Funktion ab

Um die Ableitung zu erhalten, wenden wir die Kettenregel an, bei der die Zusammensetzung von zwei Funktionen Folgendes ergibt:

ihre Ableitung ist

Oftmals wird  anstelle von
anstelle von  verwendet, es geht lediglich um die Schreibweise.
verwendet, es geht lediglich um die Schreibweise.
Wir verwenden also in unserer Aufgabe  und
und 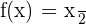 . Unsere Ableitung ist also
. Unsere Ableitung ist also
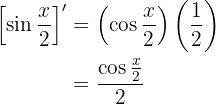
Leite folgende Funktion ab

Um die Ableitung zu erhalten, wenden wir die Kettenregel an, bei der die Zusammensetzung von zwei Funktionen Folgendes ergibt:

ihre Ableitung ist

Oftmals wird  anstelle von
anstelle von  verwendet, es geht lediglich um die Schreibweise.
verwendet, es geht lediglich um die Schreibweise.
Nun lösen wir also unsere Ableitung
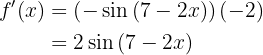
Leite folgende Funktion ab
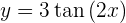
Um die Ableitung zu erhalten, wenden wir die Kettenregel an, bei der die Zusammensetzung von zwei Funktionen Folgendes ergibt:

ihre Ableitung ist

Oftmals wird  anstelle von
anstelle von  verwendet, es geht lediglich um die Schreibweise.
verwendet, es geht lediglich um die Schreibweise.
Nun lösen wir also unsere Ableitung
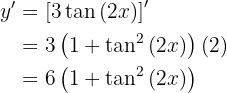
Leite folgende Funktion ab

Um die Ableitung zu erhalten, wenden wir die Kettenregel an, bei der die Zusammensetzung von zwei Funktionen Folgendes ergibt:

ihre Ableitung ist

Oftmals wird  anstelle von
anstelle von  verwendet, es geht lediglich um die Schreibweise.
verwendet, es geht lediglich um die Schreibweise.
Nun lösen wir also unsere Ableitung
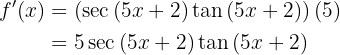
Leite folgende Funktion ab

Um die Ableitung zu erhalten, wenden wir die Kettenregel an, bei der die Zusammensetzung von zwei Funktionen Folgendes ergibt:

ihre Ableitung ist

Oftmals wird  anstelle von
anstelle von  verwendet, es geht lediglich um die Schreibweise.
verwendet, es geht lediglich um die Schreibweise.
Somit
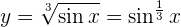
Nun lösen wir also unsere Ableitung
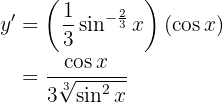
Leite folgende Funktion ab
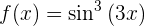
Um die Ableitung zu erhalten, wenden wir die Kettenregel an, bei der die Zusammensetzung von zwei Funktionen Folgendes ergibt:

ihre Ableitung ist

Oftmals wird  anstelle von
anstelle von  verwendet, es geht lediglich um die Schreibweise.
verwendet, es geht lediglich um die Schreibweise.
Nun lösen wir also unsere Ableitung
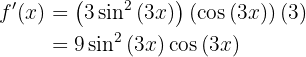
Leite folgende Funktion ab
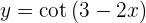
Um die Ableitung zu erhalten, wenden wir die Kettenregel an, bei der die Zusammensetzung von zwei Funktionen Folgendes ergibt:

ihre Ableitung ist

Oftmals wird  anstelle von
anstelle von  verwendet, es geht lediglich um die Schreibweise.
verwendet, es geht lediglich um die Schreibweise.
Nun lösen wir also unsere Ableitung
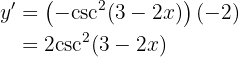
Leite folgende Funktion ab
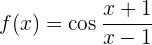
Um die Ableitung zu erhalten, wenden wir die Kettenregel an, bei der die Zusammensetzung von zwei Funktionen Folgendes ergibt:

ihre Ableitung ist

Oftmals wird  anstelle von
anstelle von  verwendet, es geht lediglich um die Schreibweise.
verwendet, es geht lediglich um die Schreibweise.
Nun lösen wir also unsere Ableitung
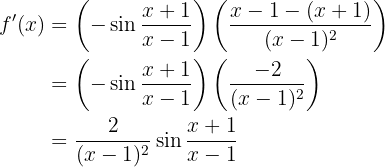
Leite folgende Funktion ab
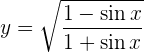
Um die Ableitung zu erhalten, wenden wir die Kettenregel an, bei der die Zusammensetzung von zwei Funktionen Folgendes ergibt:

ihre Ableitung ist

Oftmals wird  anstelle von
anstelle von  verwendet, es geht lediglich um die Schreibweise.
verwendet, es geht lediglich um die Schreibweise.
Nun lösen wir also unsere Ableitung
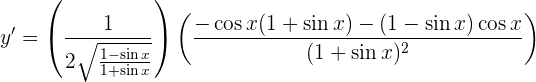
wir vereinfachen und erhalten
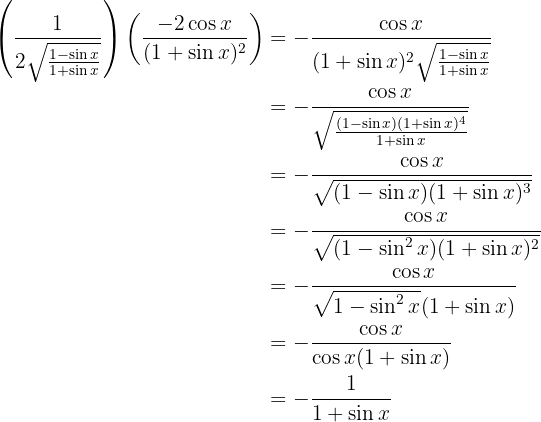
Daraus folgt:
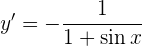
Ableitungen von trigonometrischen Umkehrfunktionen
Leite folgende Funktion ab
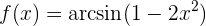
Um die Ableitung zu erhalten, wenden wir die Kettenregel an, bei der die Zusammensetzung von zwei Funktionen Folgendes ergibt:

ihre Ableitung ist

Oftmals wird  anstelle von
anstelle von  verwendet, es geht lediglich um die Schreibweise.
verwendet, es geht lediglich um die Schreibweise.
Nun lösen wir also unsere Ableitung
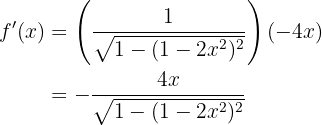
Leite folgende Funktion ab
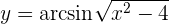
Um die Ableitung zu erhalten, wenden wir die Kettenregel an, bei der die Zusammensetzung von zwei Funktionen Folgendes ergibt:

ihre Ableitung ist

Oftmals wird  anstelle von
anstelle von  verwendet, es geht lediglich um die Schreibweise.
verwendet, es geht lediglich um die Schreibweise.
Nun lösen wir also unsere Ableitung
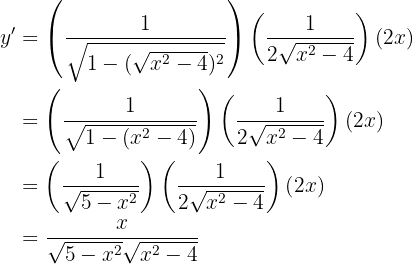
Leite folgende Funktion ab
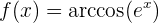
Um die Ableitung zu erhalten, wenden wir die Kettenregel an, bei der die Zusammensetzung von zwei Funktionen Folgendes ergibt:

ihre Ableitung ist

Oftmals wird  anstelle von
anstelle von  verwendet, es geht lediglich um die Schreibweise.
verwendet, es geht lediglich um die Schreibweise.
Nun lösen wir also unsere Ableitung
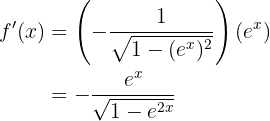
Leite folgende Funktion ab
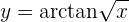
Um die Ableitung zu erhalten, wenden wir die Kettenregel an, bei der die Zusammensetzung von zwei Funktionen Folgendes ergibt:

ihre Ableitung ist

Oftmals wird  anstelle von
anstelle von  verwendet, es geht lediglich um die Schreibweise.
verwendet, es geht lediglich um die Schreibweise.
Lösen wir also unsere Ableitung
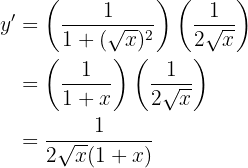
Leite folgende Funktion ab
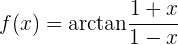
Um die Ableitung zu erhalten, wenden wir die Kettenregel an, bei der die Zusammensetzung von zwei Funktionen Folgendes ergibt:

ihre Ableitung ist

Oftmals wird  anstelle von
anstelle von  verwendet, es geht lediglich um die Schreibweise.
verwendet, es geht lediglich um die Schreibweise.
Nun lösen wir also unsere Ableitung
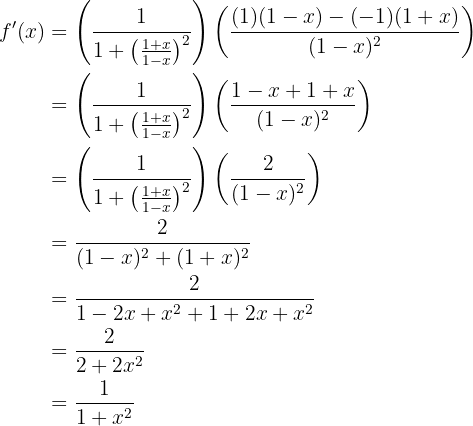
Ableitungen von zusammengesetzten Logarithmusfunktionen und trigonometrischen Funktionen
Leite folgende Funktion ab
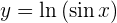
Um die Ableitung zu erhalten, wenden wir die Kettenregel an, bei der die Zusammensetzung von zwei Funktionen Folgendes ergibt:

ihre Ableitung ist

Oftmals wird  anstelle von
anstelle von  verwendet, es geht lediglich um die Schreibweise.
verwendet, es geht lediglich um die Schreibweise.
Nun lösen wir also unsere Ableitung
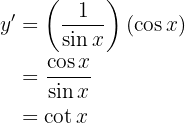
Leite folgende Funktion ab

Um die Ableitung zu erhalten, wenden wir die Kettenregel an, bei der die Zusammensetzung von zwei Funktionen Folgendes ergibt:

ihre Ableitung ist

Oftmals wird  anstelle von
anstelle von  verwendet, es geht lediglich um die Schreibweise.
verwendet, es geht lediglich um die Schreibweise.
Nun lösen wir also unsere Ableitung
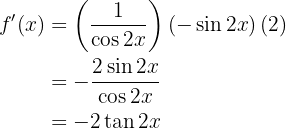
Leite folgende Funktion ab
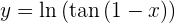
Um die Ableitung zu erhalten, wenden wir die Kettenregel an, bei der die Zusammensetzung von zwei Funktionen Folgendes ergibt:

ihre Ableitung ist

Oftmals wird  anstelle von
anstelle von  verwendet, es geht lediglich um die Schreibweise.
verwendet, es geht lediglich um die Schreibweise.
Nun lösen wir also unsere Ableitung
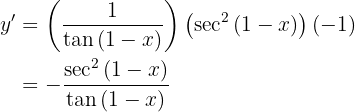
Leite folgende Funktion ab
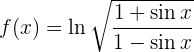
Um die Ableitung zu erhalten, wenden wir die Kettenregel an, bei der die Zusammensetzung von zwei Funktionen Folgendes ergibt:

ihre Ableitung ist

Oftmals wird  anstelle von
anstelle von  verwendet, es geht lediglich um die Schreibweise.
verwendet, es geht lediglich um die Schreibweise.
Bevor wir ableiten, sollten wir beachten, dass unsere Funktion aufgrund der Eigenschaften des Logarithmus wie folgt geschrieben werden kann

Wir nehmen

und erhalten
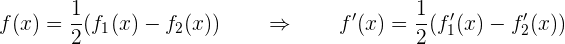
Nun lösen wir also unsere Ableitungen. Wir beginnen mit 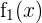
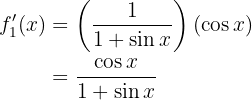
Nun leiten wir  ab
ab
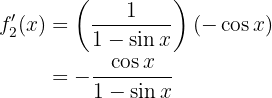
Und somit:
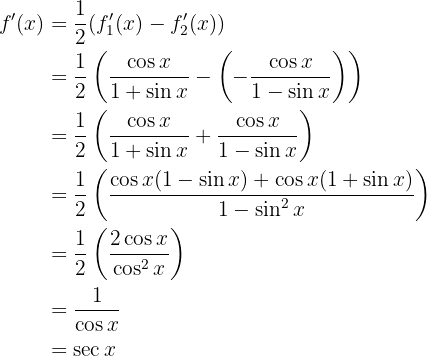
Leite folgende Funktion ab

Um die Ableitung zu erhalten, wenden wir die Kettenregel an, bei der die Zusammensetzung von zwei Funktionen Folgendes ergibt:

ihre Ableitung ist

Oftmals wird  anstelle von
anstelle von  verwendet, es geht lediglich um die Schreibweise.
verwendet, es geht lediglich um die Schreibweise.
Nun lösen wir also unsere Ableitung. Wir lösen zunächst die Ableitung der Funktion im Argument des Sinus und leiten wie folgt ab

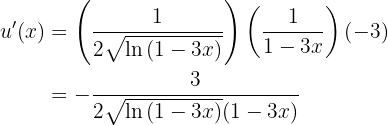
Somit:
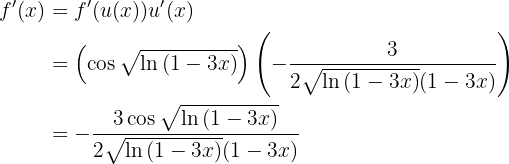
Ableitungen von zusammengesetzten Exponentialfunktionen und trigonometrischen Funktionen
Leite folgende Funktion ab
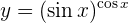
Um die Ableitung zu erhalten, wenden wir die Kettenregel an, bei der die Zusammensetzung von zwei Funktionen Folgendes ergibt:

ihre Ableitung ist

Oftmals wird  anstelle von
anstelle von  verwendet, es geht lediglich um die Schreibweise.
verwendet, es geht lediglich um die Schreibweise.
Zusätzlich zur Berücksichtigung der Kettenregel wenden wir die implizite Ableitung an, um die Ableitung von  zu ermitteln.
zu ermitteln.
Nun lösen wir also unsere Ableitung
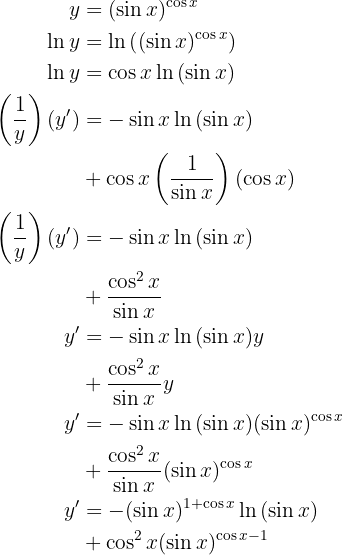
Leite folgende Funktion ab
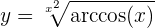

ihre Ableitung ist

Oftmals wird  anstelle von
anstelle von  verwendet, es geht lediglich um die Schreibweise.
verwendet, es geht lediglich um die Schreibweise.
Zusätzlich zur Berücksichtigung der Kettenregel wenden wir die implizite Ableitung an, um die Ableitung von  zu ermitteln.
zu ermitteln.
Wir lösen also unsere Ableitung
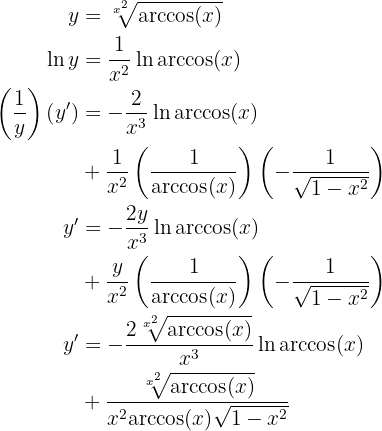
Leite folgende Funktion ab
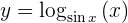
Um die Ableitung zu erhalten, wenden wir die Kettenregel an, bei der die Zusammensetzung von zwei Funktionen Folgendes ergibt:

ihre Ableitung ist

Oftmals wird  anstelle von
anstelle von  verwendet, es geht lediglich um die Schreibweise.
verwendet, es geht lediglich um die Schreibweise.
Zunächst können wir aufgrund der Eigenschaften von Logarithmen die Basis in den natürlichen Logarithmus ändern. Daraus folgt:

Und somit:
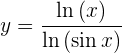
Nun wollen wir unsere Ableitung lösen, indem wir die Quotientenregel für die Ableitung anwenden
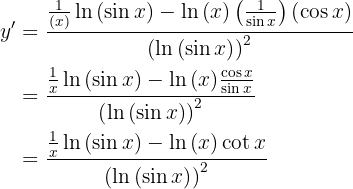
Höhere Ableitungen
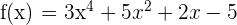
Um die Formel zu erhalten, müssen wir zunächst die ersten Ableitungen ermitteln und sehen, ob sich daraus ein Muster ergibt
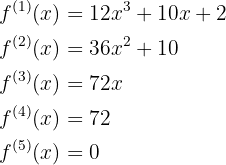
Hierbei ist zu beachten, dass die vierte Ableitung eine Konstante ist,  , sodass ab der fünften Ableitung die Ableitungen immer 0 sind, d. h.
, sodass ab der fünften Ableitung die Ableitungen immer 0 sind, d. h.


Um die Formel zu erhalten, müssen wir zunächst die ersten Ableitungen ermitteln und sehen, ob sich daraus ein Muster ergibt
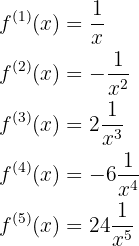
Im Allgemeinen ist die n-te Ableitung gegeben durch
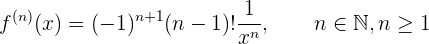
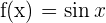
Um die Formel zu erhalten, müssen wir zunächst die ersten Ableitungen ermitteln und sehen, ob sich daraus ein Muster ergibt
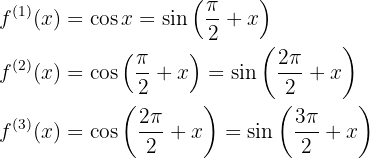
Mit diesen ersten Ableitungen erhält man, dass die n-te Ableitung die folgende Form hat
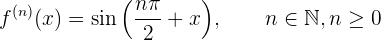

Um die Formel zu erhalten, müssen wir zunächst die ersten Ableitungen ermitteln und sehen, ob sich daraus ein Muster ergibt
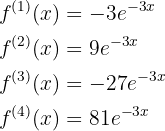
Die Formel für die n-te Ableitung ist gegeben durch
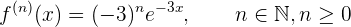
Implizite Ableitung
In den folgenden Aufgaben leiten wir implizit ab. Diese Ableitung erfolgt in der Regel, wenn wir eine Variable nicht durch eine andere ableiten können. Daher leiten wir die Variablen durch dieselbe unabhängige Variable ab, d. h. die Ableitung von  wird als
wird als  geschrieben, wann immer sie erscheint.
geschrieben, wann immer sie erscheint.

Wir leiten implizit ab. Unsere Funktion lautet

Wir leiten ab und erhalten
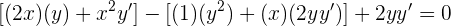
Wir schreiben die Ableitung in einer einfacheren Form
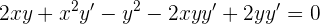
Wir lassen die Terme mit los términos con  auf der linken Seite des Ausdrucks stehen
auf der linken Seite des Ausdrucks stehen
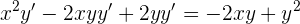
Wir können  auf der linken Seite bestimmen
auf der linken Seite bestimmen

Somit lautet unsere Ableitung

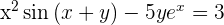
Zuerst werden wir unseren Ausdruck in eine etwas praktischere Form bringen und beginnen dann mit der Ableitung
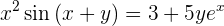
Wir leiten ab

Und vereinfachen

Wir können  auf der rechten Seite faktorisieren
auf der rechten Seite faktorisieren
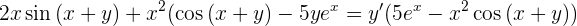
Wir erhalten das Ergebnis
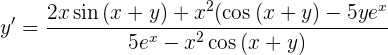
Zusätzliche Problemstellungen zur Ableitung
Leite folgende Funktion ab
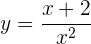
Um unsere Ableitung zu erhalten, wenden wir die Quotientenregel an
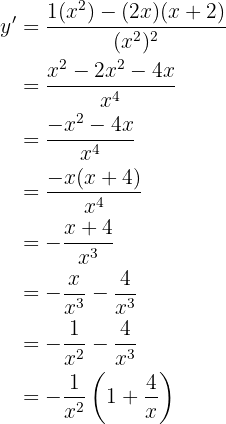
Leite folgende Funktion ab
Um die Ableitung zu erhalten, wenden wir die Kettenregel an, bei der die Zusammensetzung von zwei Funktionen Folgendes ergibt:

ihre Ableitung ist

Oftmals wird  anstelle von
anstelle von  verwendet, es geht lediglich um die Schreibweise.
verwendet, es geht lediglich um die Schreibweise.
Wir lösen nun unsere Ableitung
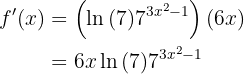
Leite folgende Funktion ab

Um die Ableitung zu erhalten, wenden wir die Kettenregel an, bei der die Zusammensetzung von zwei Funktionen Folgendes ergibt:

ihre Ableitung ist

Oftmals wird  anstelle von
anstelle von  verwendet, es geht lediglich um die Schreibeweise.
verwendet, es geht lediglich um die Schreibeweise.
Vor dem Lösen wenden wir die Eigenschaften von Logarithmen an, um den Ausdruck zu vereinfachen und etwas einfacher zu gestalten
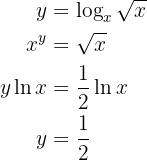
Das heißt, die Ableitung einer Konstanten ist unmittelbar
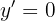
Leite folgende Funktion ab
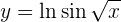
Um die Ableitung zu erhalten, wenden wir die Kettenregel an, bei der die Zusammensetzung von zwei Funktionen Folgendes ergibt:

ihre Ableitung ist

Oftmals wird  anstelle von
anstelle von  verwendet, es geht lediglich um die Schreibeweise.
verwendet, es geht lediglich um die Schreibeweise.
Nun lösen wir also unsere Ableitung
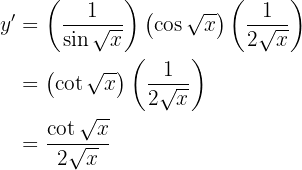
Mit KI zusammenfassen:












