Kapitel
Die Ableitung einer Funktion 
ist eine Funktion, die das Verhältnis der Änderung von 
bei 
darstellt. Aus geometrischer Sicht ist die Ableitung die Funktion, die jedem Punkt des Graphen von die Steigung der Tangente an den Graphen in diesem Punkt zuordnet.
Die Ableitung wird als 
geschrieben und wie folgt ausgedrückt
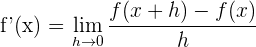
Wie wird die Ableitung berechnet?
Um die Ableitung einer Funktion zu berechnen, reicht es aus, den Grenzwert in den Ausdruck für die Ableitung einzusetzen und zu berechnen; dies kann jedoch manchmal zu Verwirrung bei der Bearbeitung des gesamten Ausdrucks führen. Aus diesem Grund ist es ratsam, die Ableitung in mehreren Schritten auszuführen
1 Berechne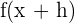 
2 Ermittle die Differenz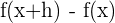 
3 Berechne den Quotienten 
4 Ermittle den Grenzwert, wenn 
gegen 
verläuft
Beispiele zur Ableitung
Beispiel 1: Berechne die Ableitung von 
mithilfe des Grenzwertes.
Um die Ableitung zu ermitteln, führen wir die folgenden vier Schritte aus
1 Berechne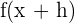
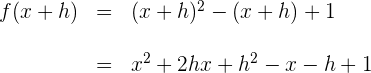
2 Berechne die Differenz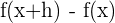
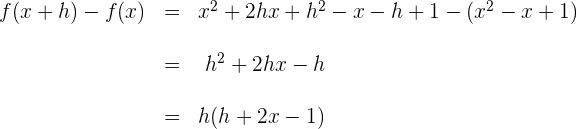
3 Berechne den Quotienten
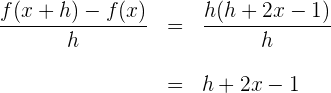
4 Bestimme den Grenzwert, wenn gegen verläuft
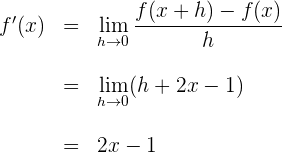
Beispiel 2: Berechne die Ableitung von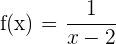 
mithilfe des Grenzwertes.
Um die Ableitung zu berechnen, führen wir die folgenden vier Schritte aus
1 Berechne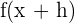
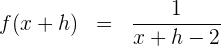
2 Berechne die Differenz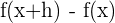
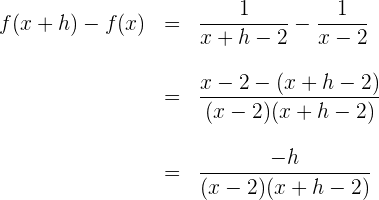
3 Berechne den Quotienten
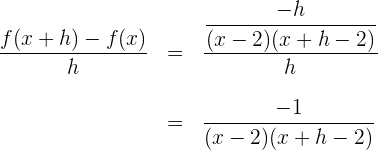
4 Ermittle den Grenzwert, wenn gegen verläuft
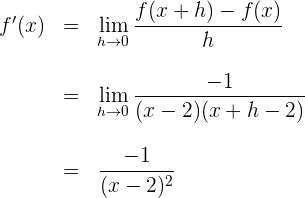
Ableitung von abschnittsweise definierten Funktionen
Bei Funktionen, die abschnittsweise definiert sind, müssen die links- und rechtsseitigen Ableitungen an den Trennpunkten der verschiedenen Abschnitte untersucht werden.
Wenn die beiden Ableitungen am fraglichen Punkt unterschiedlich sind, ist die Funktion an diesem Punkt nicht ableitbar.
Beispiel 1: Untersuche die Ableitbarkeit der Funktion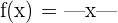 
.
1 Wir schreiben die Funktion als abschnittsweise definierte Funktion
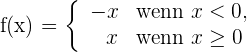
2 Wir berechnen die links- und rechtsseitigen Ableitungen vom Punkt 
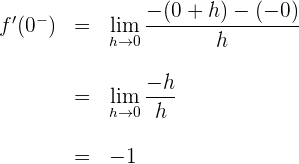
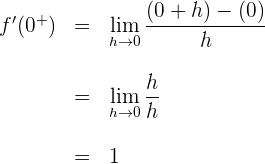
Wenn die links- und rechtsseitigen Ableitungen von 
unterschiedlich sind, ist die Funktion am gegebenen Punkt nicht ableitbar.
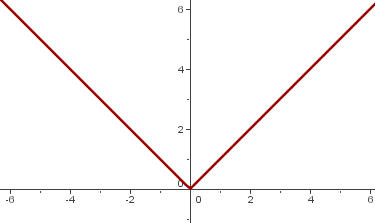
Beispiel 2: Untersuche die Ableitbarkeit der Funktion
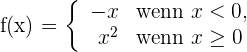
1 Wir berechnen die links- und rechtsseitigen Ableitungen vom Punkt
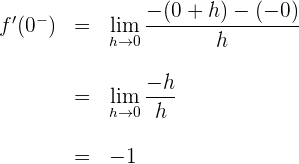
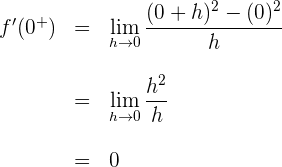
Wenn die links- und rechtsseitigen Ableitungen von unterschiedlich sind, ist die Funktion am gegebenen Punkt nicht ableitbar.
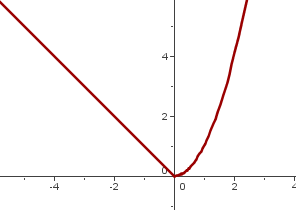
Beispiel 3: Untersuche die Ableitbarkeit der Funktion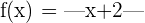 
.
1 Wir schreiben als abschnittsweise definierte Funktion
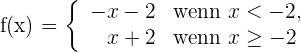
2 Wir berechnen die links- und rechtsseitigen Ableitungen vom Punkt 
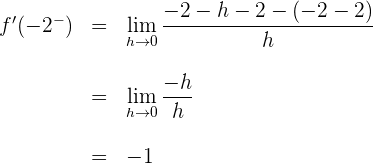
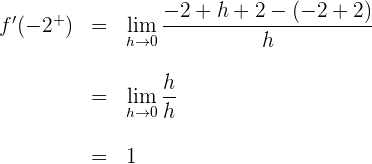
Wenn die links- und rechtsseitigen Ableitungen von 
unterschiedlich sind, ist die Funktion am gegebenen Punkt nicht ableitbar.
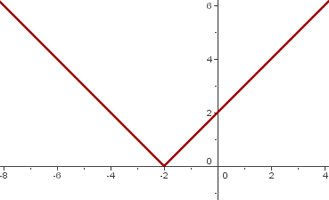
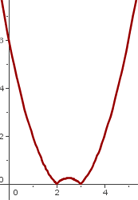
Beispiel 4: Untersuche die Ableitbarkeit der Funktion 
.
1 Wir schreiben als abschnittsweise definierte Funktion
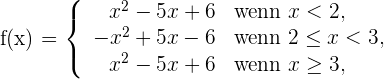
2 Wir berechnen die links- und rechtsseitigen Ableitungen am Punkt 
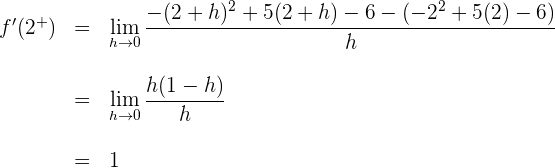
Wenn die links- und rechtsseitigen Ableitungen von 
unterschiedlich sind, ist die Funktion am gegebenen Punkt nicht ableitbar.
Wir berechnen die links- und rechtsseitigen Ableitungen am Punkt 
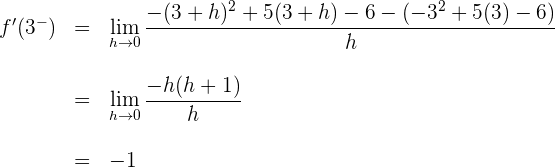
Wenn die links- und rechtsseitigen Ableitungen von 
unterschiedlich sind, ist die Funktion am gegebenen Punkt nicht ableitbar.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
