Kapitel

Definition der Ableitung
Es gibt mehrere Möglichkeiten, die Ableitung zu definieren, sie haben mit Geometrie, Physik und Wirtschaft zu tun, aber letztlich sind sie alle gleich.
Aus geometrischer Sicht stellt die Ableitung die Steigung der Tangente an den Graphen der Funktion dar. Die Ableitung der Funktion  ist gegeben durch
ist gegeben durch
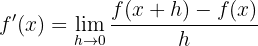
Die Ableitung von  existiert, wenn der Grenzwert existiert; gibt es keinen Grenzwert, so gibt es auch keine Ableitung
existiert, wenn der Grenzwert existiert; gibt es keinen Grenzwert, so gibt es auch keine Ableitung
Aufgabe zur Ableitung einer linearen Funktion
Berechne die Ableitung anhand der Grenzwerte von 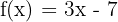
1Wir ermitteln 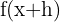

2Wir berechnen den Quotienten aus der Definition der Ableitung und vereinfachen
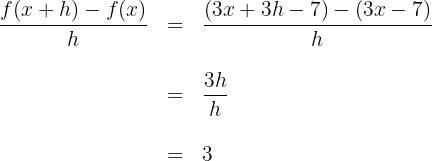
3Die Ableitung ergibt sich aus der Berechnung des Grenzwerts, wenn  gegen 0 zum obigen Quotienten konvergiert
gegen 0 zum obigen Quotienten konvergiert
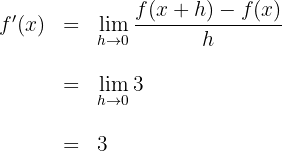
Aufgaben zu Ableitungen quadratischer Funktionen
Berechne die Ableitung anhand der Grenzwerte von 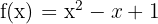
1Wir ermitteln 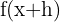
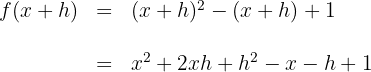
2Wir berechnen den Quotienten aus der Definition der Ableitung und vereinfachen
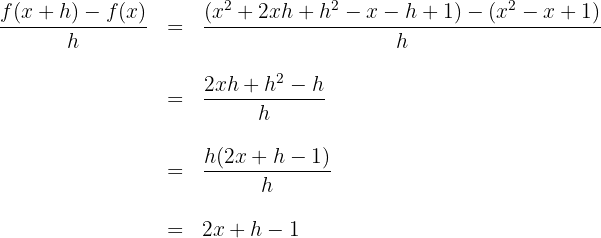
3Die Ableitung ergibt sich aus der Berechnung des Grenzwerts, wenn  gegen 0 zum obigen Quotienten konvergiert
gegen 0 zum obigen Quotienten konvergiert

Berechne die Ableitung anhand der Grenzwerte von 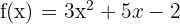
1Wir ermitteln 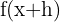
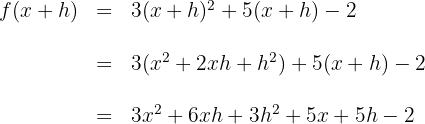
2Wir berechnen den Quotienten aus der Definition der Ableitung und vereinfachen

3Die Ableitung ergibt sich aus der Berechnung des Grenzwerts, wenn  gegen 0 konvergiert zum obigen Quotienten konvergiert
gegen 0 konvergiert zum obigen Quotienten konvergiert

Aufgaben zu Ableitungen kubischer Funktionen
Berechne die Ableitung anhand der Grenzwerte von 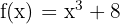
1Wir ermitteln 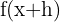

2Wir berechnen den Quotienten aus der Definition der Ableitung und vereinfachen
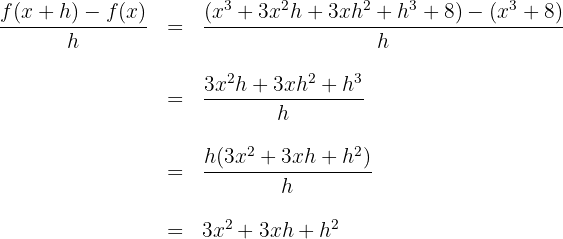
3Die Ableitung ergibt sich aus der Berechnung des Grenzwerts, wenn  gegen 0 zum obigen Quotienten konvergiert
gegen 0 zum obigen Quotienten konvergiert
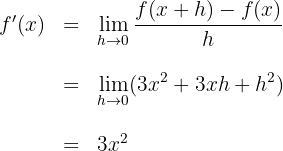
Berechne die Ableitung anhand der Grenzwerte von 
1Wir ermitteln 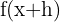
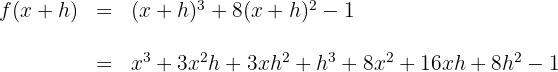
2Wir berechnen den Quotienten aus der Definition der Ableitung und vereinfachen
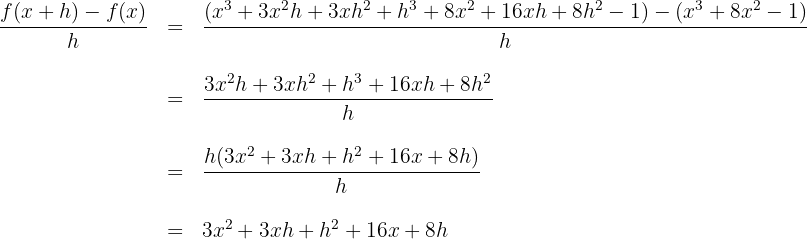
3Die Ableitung ergibt sich aus der Berechnung des Grenzwerts, wenn  gegen 0 zum obigen Quotienten konvergiert
gegen 0 zum obigen Quotienten konvergiert
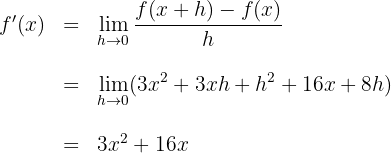
Aufgaben zur Ableitung von Quotienten
Berechne die Ableitung anhand der Grenzwerte von 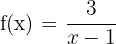
1Wir ermitteln 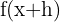

2Wir berechnen den Quotienten aus der Definition der Ableitung und vereinfachen
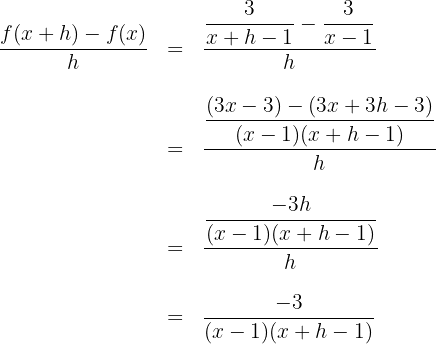
3Die Ableitung ergibt sich aus der Berechnung des Grenzwerts, wenn  gegen 0 zum obigen Quotienten konvergiert
gegen 0 zum obigen Quotienten konvergiert

Berechne die Ableitung anhand der Grenzwerte von 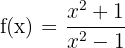
1Wir ermitteln 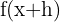

2Wir berechnen den Quotienten aus der Definition der Ableitung und vereinfachen

3Die Ableitung ergibt sich aus der Berechnung des Grenzwerts, wenn  gegen 0 zum obigen Quotienten konvergiert
gegen 0 zum obigen Quotienten konvergiert

Aufgaben zu Ableitungen von Wurzeln
Berechne die Ableitung anhand der Grenzwerte von 
1Wir ermitteln 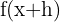

2Wir berechnen den Quotienten aus der Definition der Ableitung und rationalisieren, um mit dem Nenner  zu rechnen
zu rechnen
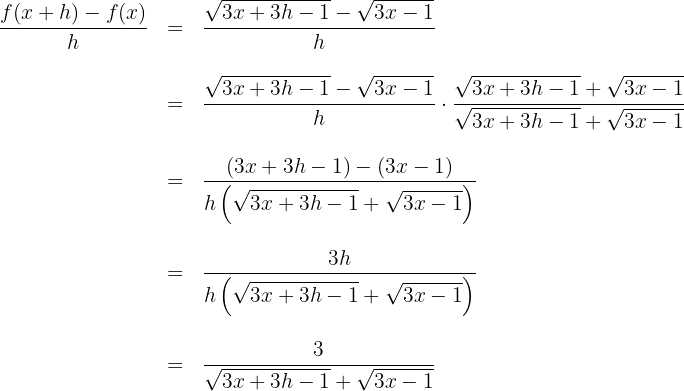
3Die Ableitung ergibt sich aus der Berechnung des Grenzwerts, wenn  gegen 0 zum obigen Quotienten konvergiert
gegen 0 zum obigen Quotienten konvergiert
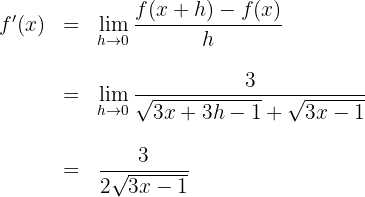
Berechne die Ableitung anhand der Grenzwerte von 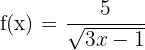
1Wir ermitteln 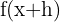
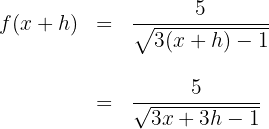
2Wir berechnen den Quotienten aus der Definition der Ableitung und rationalisieren, um mit dem Nenner  zu rechnen
zu rechnen
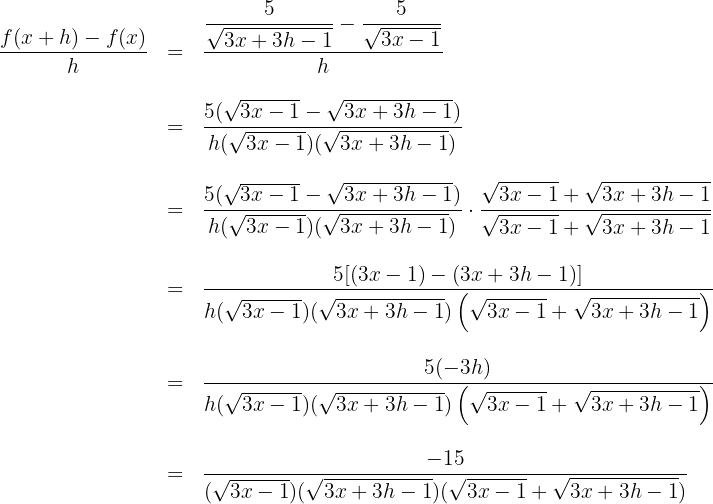
3Die Ableitung ergibt sich aus der Berechnung des Grenzwerts, wenn  gegen 0 zum obigen Quotienten konvergiert
gegen 0 zum obigen Quotienten konvergiert
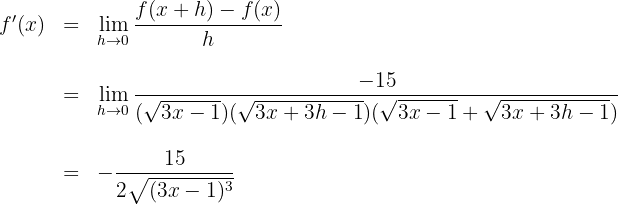
Aufgabe, bei der keine Ableitung existiert
Berechne die Ableitung anhand der Grenzwerte von 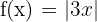 en
en 
1Wir ermitteln 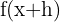

2Wir berechnen den Quotienten aus der Definition der Ableitung
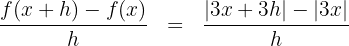
3Die Ableitung ergibt sich aus der Berechnung des Grenzwerts, wenn  gegen 0 zum obigen Quotienten bei
gegen 0 zum obigen Quotienten bei  konvergiert
konvergiert
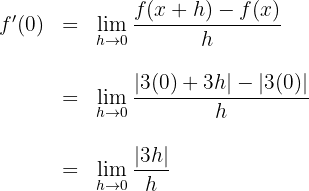
4Die Betragsfunktion wird wie folgt ausgedrückt
nicht gleich

Die Ableitung von  existiert daher bei
existiert daher bei  nicht
nicht
Mit KI zusammenfassen:












