Geometrische Interpretation der Ableitung
Geometrisch ist die Ableitung einer Funktion 
an einem Punkt 
die Steigung der
Tangente an , die durch den Punkt verläuft.
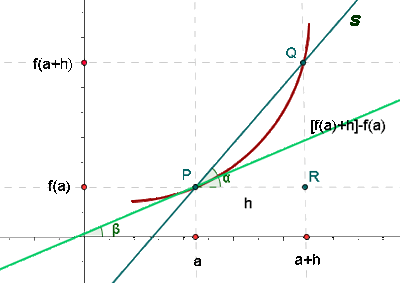
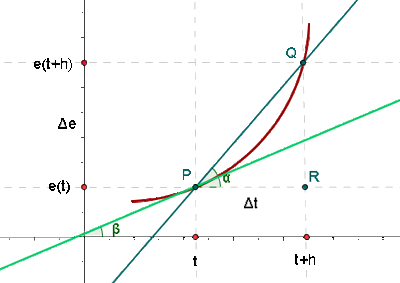
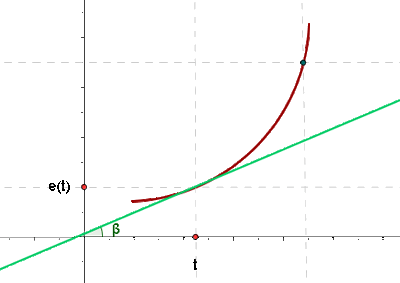
Wir sehen uns die Abbildung an: Wir nehmen die Punkte 
und 
und verbinden sie durch eine Sekante. Diese Sekante bildet einen Winkel 
mit der Horizontalen. Da wir die Steigung der Tangente berechnen möchten, stellen wir fest, dass dieser Wert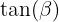 
ist, wobei
der Winkel zwischen der 
-Achse und der Tangente ist.
Wir kehren zum Winkel zurück, für den gilt:
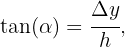
wobei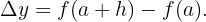 
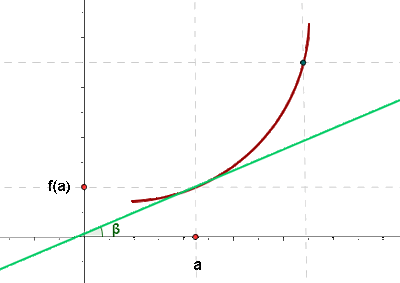
Wenn der Wert 
gegen 
konvergiert, wird der Punkt oftmals mit dem Punkt verwechselt. Dann ist die Sekante tendenziell die Tangente an die Funktion in und daher ist der Winkel tendenziell 
.
Daraus folgt, dass
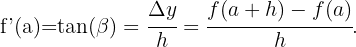
Beispiele
Gegeben ist 
. Berechne die Punkte, in denen die Tangente parallel zur Winkelhalbierenden des 1. Quadranten ist.
Die Gleichung der Winkelhalbierenden des ersten Quadranten ist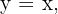 
ihre Steigung ist also 
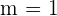. Da die beiden Geraden parallel sind, haben sie die gleiche Steigung: 
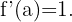Da die Steigung der Tangente an den Graphen gleich der Ableitung im Punkt 
ist.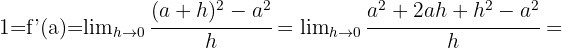
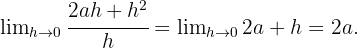Daraus folgt, dass 
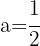und durch Einsetzen in die Funktion erhalten wir den gesuchten Punkt 
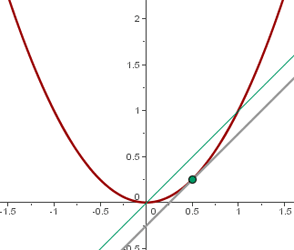
Gegeben ist der Graph der Gleichung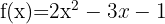 
. Ermittle die Koordinaten der Punkte auf dieser Kurve, in denen die Tangente mit der x-Achse einen Winkel von 
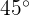bildet.
Aus der geometrischen Interpretation der Ableitung ergibt sich, dass 
Nun bestimmen wir anhand der Formel für die Ableitung den Wert von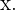 
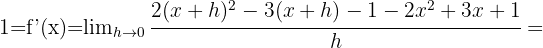
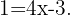Somit ist 
und wir setzen schließlich in die Funktion ein. Daraus folgt, dass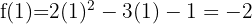 
und der gesuchte Punkt ist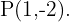 
Ermittle die Werte des Parameters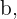 
so dass die Tangenten an den Graphen der Funktion 
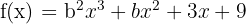an den Punkten 
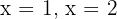auf der x-Achse parallel sind.
Damit sie parallel sind, müssen die Ableitungen für 
und 
gleich sein. Die Ableitung der Funktion ist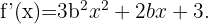 
Somit: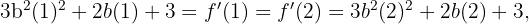 
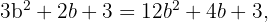
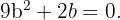Letzteres impliziert, dass 
oder 
Interpretation der Ableitung in der Physik
Durchschnittsgeschwindigkeit
Die Durchschnittsgeschwindigkeit ist der Quotient aus der zurückgelegten Strecke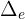 
und der vergangenen Zeit 
Wenn die Strecke durch eine Funktion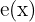 
bestimmt wird und wir eine verstrichene Zeit 
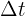betrachten, erhalten wir folgende Formel für die Durchschnittsgeschwindigkeit: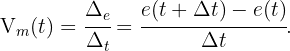 
Momentangeschwindigkeit
Die Momentangeschwindigkeit ist der Grenzwert der Geschwindigkeit, wenn 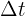gegen 0 konvergiert. Das heißt, die Ableitung der Strecke in Bezug auf die Zeit.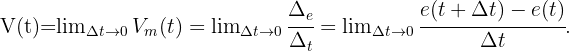 
Beispiele
Das Verhältnis zwischen der von einem Fahrzeug zurückgelegten Strecke in Metern und der Zeit in Sekunden ist 
. Berechne:
- Die Durchschnittsgeschwindigkeit zwischen
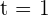und 
- Die Momentangeschwindigkeit für
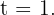
- Die Durchschnittsgeschwindigkeit ist der inkrementelle Quotient auf dem Intervall
- Die Momentangeschwindigkeit ist die Ableitung in
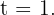
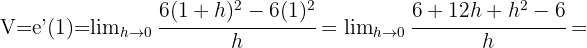
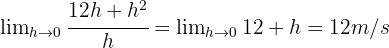
Wie hoch ist die Geschwindigkeit eines Fahrzeugs, das sich gemäß der Gleichung 
in der fünften Sekunde seiner Fahrt bewegt?
Die Entfernung wird in Metern und die Zeit in Sekunden gemessen.
Wir müssen nur die Momentangeschwindigkeit zu dem Zeitpunkt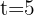 
berechnen: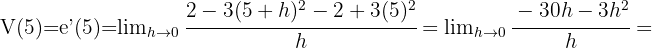 
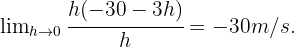
Eine bakterielle Population hat eine Wachstumsrate, die durch die Funktion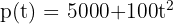 
gegeben ist, wobei 
die in Stunden gemessene Zeit ist. Es wird verlangt:
- Die Durchschnittsgeschwindigkeit der Wachstumsrate.
- Die Momentangeschwindigkeit der Wachstumsrate
- Die Momentangeschwindigkeit der Wachstumsrate für
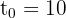Stunden.
- Dies wird durch die folgende Formel beschrieben:
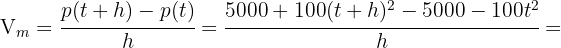
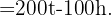
- Dies ist durch den folgenden Grenzwert gegeben:
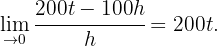
- Wir müssen lediglich die obige Formel in
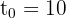auswerten. Wir erhalten 
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
