Kapitel
Die Tabelle der Ableitungen wurde von Charles Goodheart an der London School of Economics im Jahr 1947 eingeführt. Eine Ableitung ist ein Begriff, der sich auf eine Beziehung zwischen zwei oder mehreren Variablen bezieht. Eines der wichtigsten Konzepte von Ableitungen ist, dass sie gleich sind, wenn sie durch eine andere Konstante ausgedrückt werden. Es ist zwar auch möglich, die Ableitungen einer Funktion zu bestimmen, aber das kann sehr schwierig sein, weil Funktionen oftmals komplexe Bedingungen mit sich bringen.
Eine Tabelle der Ableitungen hilft dir, den Wert einer bestimmten Größe zu bestimmen, indem du feststellst, wie sich die Eingangsvariable auf die Ausgangsvariable auswirkt. In vielen Fällen hilft eine Ableitungsberechnung dabei, das Verhalten einer bestimmten Gleichung oder eines Integrals vorherzusagen. Für viele Anleger*innen ist es wichtig, über Veränderungen auf dem Aktienmarkt informiert zu sein, so dass sie beispielsweise die Ableitungstabelle als Instrument zur Bestimmung des Wertes von Aktien nutzen können.
Eine Ableitungstabelle kann auch zum Zeichnen einer Trendlinie verwendet werden, da sie eine Linie für jede Variable darstellen kann, die mit der Zeit in Beziehung steht. Die zeitliche Korrelation zwischen zwei Variablen ist für jeden Zeitabschnitt dieselbe, was das Zeichnen einer Trendlinie erleichtert.
Tabelle der gängisten Ableitungen
Nachfolgend findest du eine Tabelle mit einigen der am häufigsten in Lehrbüchern vorgestellten Funktionen und ihrer Ableitung:
| Funktion | Ableitung |
|---|---|
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
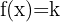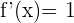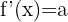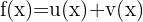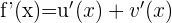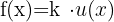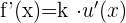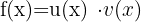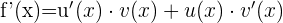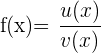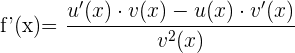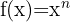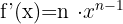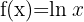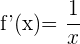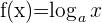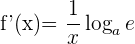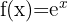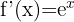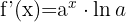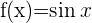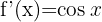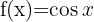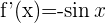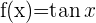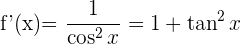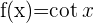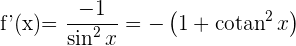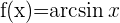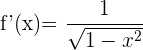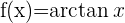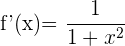Darüber hinaus klassifizieren wir in den folgenden Abschnitten die Ableitungsformeln:
Direkte Ableitungen
Ableitung Konstante
Ableitung von x
Ableitung affine Funktion
Ableitung Potenz
Ableitung Wurzel
Ableitung Quadratwurzel
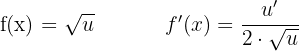
Ableitung Summe
Ableitung Produkt aus Konstante und Funktion
Ableitung Produkt
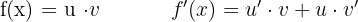
Ableitung Konstante dividiert durch Funktion
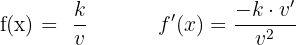
Ableitung Quotient
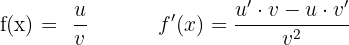
Exponential- und Logarithmusableitungen
Ableitung Exponentialfunktion
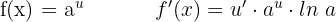
Ableitung Exponentialfunktion mit der Basis e
Ableitung Logarithmus
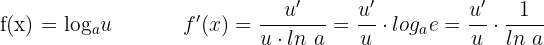
Ableitung natürlicher Logarithmus
Ableitungen trigonometrischer Funktionen
Ableitung Sinus
Ableitung Kosinus
Ableitung Tangens
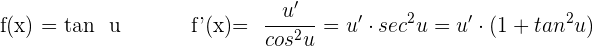
Ableitung Kotangens
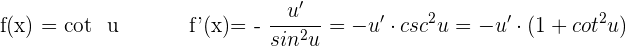
Ableitung Sekans
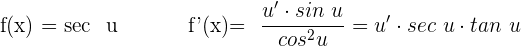
Ableitung Kosekans
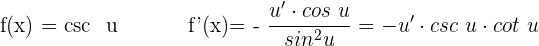
Ableitungen von trigonometrischen Umkehrfunktionen
Ableitung Arkussinus
Ableitung Arkuskosinus
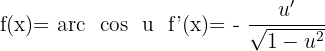
Ableitung Arkustangens
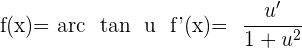
Ableitung Arkuskotangens
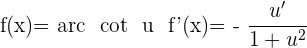
Ableitung Arkussekans
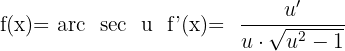
Ableitung Arkuskosekans
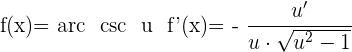
Ableitung Potenzfunktion - Exponentialfunktion
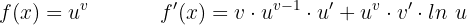
Kettenregel
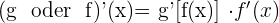
Formel der impliziten Ableitung
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
