In diesem Abschnitt werden wir uns mit der Ableitung des Tangens befassen und einige Aufgaben lösen, um ein besseres Verständnis zu erhalten.
Wir denken daran, dass der Tangens wie folgt definiert wird
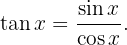
Um seine Ableitung zu berechnen, reicht es daher aus, die Ableitungsformel für Quotienten von Funktionen und die Ableitung von Sinus und Kosinus zu kennen. Fahren wir nun mit der Ableitung fort
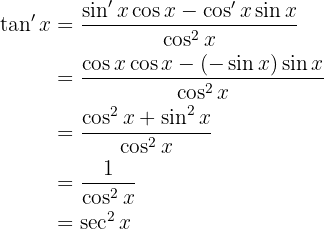
Somit haben wir
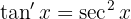
Oder auch mit der Kettenregel
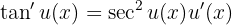
Wir sehen uns einige Beispiele an, in denen wir die Ableitung des Tangens nutzen. Mehrfach werden wir die Kettenregel anwenden. Falls du diese Methode noch nicht kennst, empfehlen wir dir, unseren Artikel zu diesem Thema zu lesen.
Leite die folgende Funktion ab

Wir integrieren
Wir stellen fest, dass wir in diesem Fall 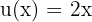 und
und 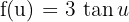 nehmen können. Wir erhalten also
nehmen können. Wir erhalten also
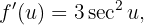
während

Unsere Ableitung lautet somit

Leite die folgende Funktion ab

Wir stellen fest, dass wir in diesem Fall 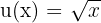 und
und 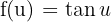 nehmen können. Wir erhalten also
nehmen können. Wir erhalten also
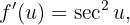
während
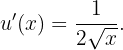
Unsere Ableitung lautet somit
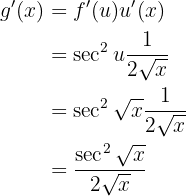
Leite die folgende Funktion ab

In diesem Fall haben wir eine dreifache Zusammensetzung, daher wenden wir die Kettenregel dreimal an. Als Erstes nehmen wir
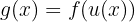 ,
,
wobei 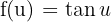 und
und  . Wir haben
. Wir haben
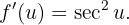
Nun leiten wir  ab. Wir stellen allerdings fest, dass wir
ab. Wir stellen allerdings fest, dass wir  auch als Zusammensetzung ausdrücken können, wobei
auch als Zusammensetzung ausdrücken können, wobei 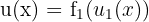 ,
,  und
und  . Ihre Ableitungen lauten
. Ihre Ableitungen lauten
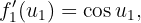
wobei wir  auch als Zusammensetzung ausdrücken können, wobei
auch als Zusammensetzung ausdrücken können, wobei  ,
, 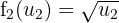 und
und 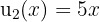 . Ihre Ableitungen lauten
. Ihre Ableitungen lauten
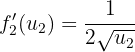
und

Somit lautet unsere Ableitung
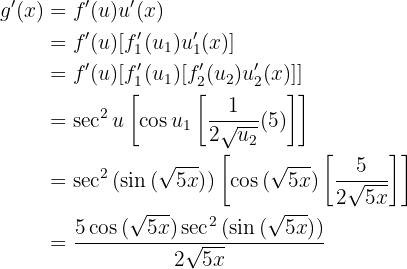
Mit KI zusammenfassen:


