Willkommen zu dieser Übungsreihe über Anwendungen der Ableitung! Wir werden untersuchen, wie man die Ableitung, ein grundlegendes Werkzeug in der Berechnung, verwenden kann, um eine Vielzahl von Problemen aus der realen Welt zu lösen. Ableitungen ermöglichen es uns zu verstehen, wie sich Funktionen in Abhängigkeit von einer Variablen verändern und sind in Bereichen wie Physik, Wirtschaft, Biologie und vielen anderen Disziplinen unerlässlich.
Mach dich bereit, deine mathematischen Fähigkeiten einzusetzen und herauszufinden, wie Ableitungen uns helfen können, Maxima und Minima zu verstehen und zu lösen!
Bestimme die Intervalle des Monotonieverhaltens der folgenden Funktion:
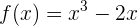
Die Definitionsmenge von  ist
ist
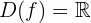
Um die Intervalle zu bestimmen, in denen der Graph der Funktion steigt, müssen wir die Intervalle ermitteln, in denen die Ableitung positiv ist. Und um die Intervalle zu bestimmen, in denen der Graph der Funktion fällt, müssen wir die Intervalle ermitteln, in denen die Ableitung negativ ist. Daher müssen wir zunächst die Funktion ableiten:
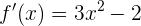
Wir ermitteln nun die Intervalle, in denen  positiv oder negativ ist. Hierzu berechnen wir die Nullstellen von
positiv oder negativ ist. Hierzu berechnen wir die Nullstellen von  :
:
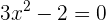
Da 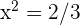 , erhalten wir
, erhalten wir 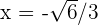 und
und 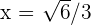 .
.
Beachte, dass mit der Ableitung  ein Vorzeichenwechsel einhergeht.
ein Vorzeichenwechsel einhergeht.
Wenn also 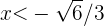 (das heißt
(das heißt  ), dann
), dann 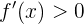 ). Um dies feststellen zu können, probieren wir (zum Beispiel) mit
). Um dies feststellen zu können, probieren wir (zum Beispiel) mit  , wodurch wir
, wodurch wir 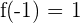 erhalten.
erhalten.
Und wenn 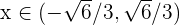 , ist
, ist 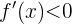 .
.
Und schließlich, wenn  , ist
, ist 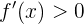 .
.
Somit sind die Intervalle, in denen die Funktion  streng monoton steigend ist,
streng monoton steigend ist,
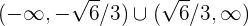
Die Intervalle, in denen  streng monoton fallend ist, sind
streng monoton fallend ist, sind
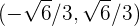
Ermittle die Intervalle des Monotonieverhaltens der folgenden Funktion:
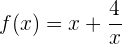
Die Definitionsmenge von  ist
ist
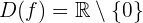
Die Funktion ist also für die Zahl 0 nicht definiert.
Um die Intervalle zu bestimmen, in denen der Graph der Funktion steigt, müssen wir die Intervalle ermitteln, in denen die Ableitung positiv ist. Und um die Intervalle zu bestimmen, in denen der Graph der Funktion fällt, müssen wir die Intervalle ermitteln, in denen die Ableitung negativ ist. Daher müssen wir zunächst die Funktion ableiten:

Um nun die Intervalle bestimmen zu können, in denen  positiv oder negativ ist, müssen wir zunächst die Nullstellen von
positiv oder negativ ist, müssen wir zunächst die Nullstellen von  ermitteln:
ermitteln:

Wir erhalten somit 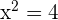 , weshalb
, weshalb  und
und  . Außerdem müssen wir beachten, dass
. Außerdem müssen wir beachten, dass  und
und  dort nicht definiert ist.
dort nicht definiert ist.
Die Logik, der wir hier folgen, ist, dass  das Vorzeichen um die Nullstellen oder Punkte der Unbestimmtheit ändert.
das Vorzeichen um die Nullstellen oder Punkte der Unbestimmtheit ändert.
Wir stellen fest, dass wenn 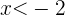 (das heißt
(das heißt 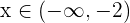 ), ist
), ist 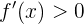 . Um dies feststellen zu können, probieren wir (zum Beispiel) mit
. Um dies feststellen zu können, probieren wir (zum Beispiel) mit  , wodurch wir
, wodurch wir 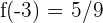 erhalten.
erhalten.
Und wenn 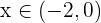 , ist
, ist 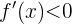 .
.
Wenn  , ist
, ist 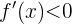 .
.
Und wenn 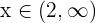 , ist
, ist 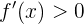 .
.
Die Intervalle, in denen  streng monoton steigend ist, sind
streng monoton steigend ist, sind

Die Intervalle, in denen  streng monoton fallend ist, sind
streng monoton fallend ist, sind
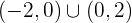
Bestimme die Maxima und Minima der folgenden Funktion:
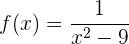
Um die Maxima und Minima der Funktion zu bestimmen, müssen wir die Ableitung der Funktion berechnen.

Die Funktion hat ein Maximum oder Minimum, wenn 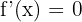 . Das heißt
. Das heißt
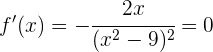 ,
,
was erfüllt ist, wenn 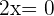 . Und somit
. Und somit  .
.
Um bestimmen zu können, ob  ein Maximum ist, können wir die 1. oder 2. Ableitung nutzen. In diesem Fall ist es einfacher, die 1. Ableitung zu verwenden, um die Berechnung der 2. Ableitung zu vermeiden. Hierfür werten wir
ein Maximum ist, können wir die 1. oder 2. Ableitung nutzen. In diesem Fall ist es einfacher, die 1. Ableitung zu verwenden, um die Berechnung der 2. Ableitung zu vermeiden. Hierfür werten wir  an einem Punkt links von
an einem Punkt links von  und an einem Punkt rechts davon aus (nur nicht bei -3 und 3). Da -1 links von
und an einem Punkt rechts davon aus (nur nicht bei -3 und 3). Da -1 links von  liegt, prüfen wir:
liegt, prüfen wir:
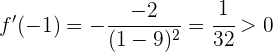
Da 1 rechts von  liegt, prüfen wir:
liegt, prüfen wir:
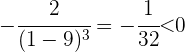
Wir stellen fest, dass die Ableitung links von  positiv ist (die Funktion steigt) und rechts von
positiv ist (die Funktion steigt) und rechts von  negativ ist (die Funktion fällt).
negativ ist (die Funktion fällt).
Der Wert von  bei
bei  ist:
ist:
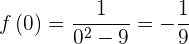
Dies bedeutet, dass 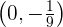 ein Maximum (und der einzige Extrempunkt von
ein Maximum (und der einzige Extrempunkt von  ) ist.
) ist.
Ermittle die Maxima und Minima der folgenden Funktion:

Um die Maxima und Minima der Funktion zu bestimmen, müssen wir die Ableitung der Funktion berechnen.
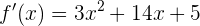
Die Funktion hat ein Maximum oder Minimum, wenn 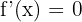 . Das heißt
. Das heißt
 ,
,
was erfüllt ist, wenn  .
.
Um bestimmen zu können, ob 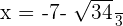 ein Maximum ist, können wir die 1. oder 2. Ableitung nutzen. In diesem Fall ist es einfacher, die 1. Ableitung zu verwenden, um die Berechnung der 2. Ableitung zu vermeiden. Hierfür werten wir
ein Maximum ist, können wir die 1. oder 2. Ableitung nutzen. In diesem Fall ist es einfacher, die 1. Ableitung zu verwenden, um die Berechnung der 2. Ableitung zu vermeiden. Hierfür werten wir  an einem Punkt links von
an einem Punkt links von 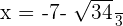 und an einem Punkt rechts davon aus. Da -6 links von
und an einem Punkt rechts davon aus. Da -6 links von  liegt, prüfen wir:
liegt, prüfen wir:
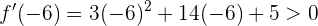
Da -4 rechts von  liegt, prüfen wir::
liegt, prüfen wir::
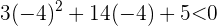
Wir stellen fest, dass die Ableitung links von  positiv (die Funktion steigt) und rechts von
positiv (die Funktion steigt) und rechts von  negativ (die Funktion fällt) ist.
negativ (die Funktion fällt) ist.
Der Wert von  bei
bei  ist:
ist:
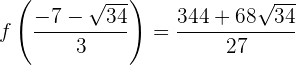
Dies bedeutet, dass 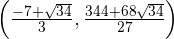 ein Maximum von
ein Maximum von  ist.
ist.
Um bestimmen zu können, ob 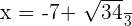 ein Minimum ist, können wir die 2. oder 1. Ableitung nutzen. In diesem Fall ist es einfacher, die 1. Ableitung zu verwenden, um die Berechnung der 2. Ableitung zu vermeiden. Hierfür werten wir
ein Minimum ist, können wir die 2. oder 1. Ableitung nutzen. In diesem Fall ist es einfacher, die 1. Ableitung zu verwenden, um die Berechnung der 2. Ableitung zu vermeiden. Hierfür werten wir  an einem Punkt links von
an einem Punkt links von 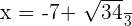 aus. Wir wie zuvor gesehen haben, ist
aus. Wir wie zuvor gesehen haben, ist 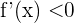 .
.
Da 2 außerdem rechts von  liegt, prüfen wir:
liegt, prüfen wir:
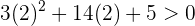
Wir stellen fest, dass die Ableitung links von  negativ (die Funktion fällt) und rechts von
negativ (die Funktion fällt) und rechts von  positiv ist (die Funktion steigt).
positiv ist (die Funktion steigt).
Der Wert von  bei
bei  ist:
ist:

Dies bedeutet, dass 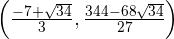 ein Maximum von
ein Maximum von  ist.
ist.
Bestimme die Maxima und Minima der folgenden Funktion:
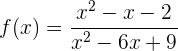
Um die Maxima und Minima der Funktion zu bestimmen, müssen wir die Ableitung der Funktion berechnen. Wir stellen fest, dass wir die Funktion wie folgt vereinfachen können:

Die Ableitung ist also:
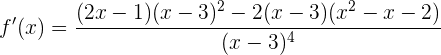
Wir vereinfachen den Zähler und erhalten:
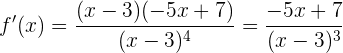
Die Funktion hat ein Maximum oder Minimum, wenn 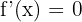 . Das heißt
. Das heißt
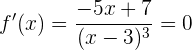 ,
,
was erfüllt ist, wenn 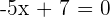 . Und somit
. Und somit 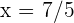 .
.
Um bestimmen zu können, ob determianr si 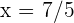 ein Maximum ist, können wir die 2. oder 1. Ableitung nutzen. In diesem Fall ist es jedoch einfacher, die 1. Ableitung zu verwendnen, um die Berechnung der 2. Ableitung zu vermeiden. Hierfür werten wir
ein Maximum ist, können wir die 2. oder 1. Ableitung nutzen. In diesem Fall ist es jedoch einfacher, die 1. Ableitung zu verwendnen, um die Berechnung der 2. Ableitung zu vermeiden. Hierfür werten wir  an einem Punkt links von
an einem Punkt links von 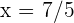 und an einem Punkt rechts davon aus (jedoch niemals größer als 3). Da 1 links von
und an einem Punkt rechts davon aus (jedoch niemals größer als 3). Da 1 links von  liegt, prüfen wir:
liegt, prüfen wir:
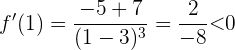
Da 2 außerdem rechts von  liegt, prüfen wir:
liegt, prüfen wir:
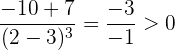
Wir stellen fest, dass die Ableitung links von  negativ (die Funktion fällt) und rechts von
negativ (die Funktion fällt) und rechts von  positiv ist (die Funktion steigt).
positiv ist (die Funktion steigt).
Der Wert von  bei
bei  ist:
ist:

Dies bedeutet, dass 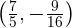 ein Minimum (und der einzige Extrempunkt von
ein Minimum (und der einzige Extrempunkt von  ) ist.
) ist.
Bestimme die Gleichung der Tangente sowie die allgemeine Gleichung der Geraden für  der folgenden Funktion:
der folgenden Funktion:
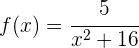
Die 1. Ableitung ist gegeben durch:
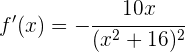
Die Steigung der Tangente für  ist gegeben durch
ist gegeben durch

Die Funktion von  ist
ist

Daher verläuft die Funktion durch den Punkt 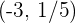 und die Tangente muss durch denselben Punkt verlaufen.
und die Tangente muss durch denselben Punkt verlaufen.
1 Um die Gleichung der Tangente zu bestimmen, verwenden wir die Punkt-Steigungs-Formel mit  und
und  :
:

Die Gleichung der Tangente ist also
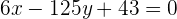
2 Um nun die Gleichung der Geraden zu bestimmen, gehen wir ganz ähnlich vor, nun aber mit 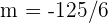 und
und  :
:
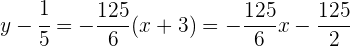
Die Gleichung der Geraden ist somit
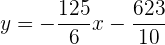
oder

Bestimme die Gleichung der Tangente und die allgemeine Geradengleichung am Wendepunkt der folgenden Funktion:

Zunächst müssen wir den Wendepunkt der der Ableitung finden. Diesen ermitteln wir mit der 2. Ableitung der Funktion. Die 1. Ableitung ist gegeben durch

Die 2. Ableitung ist gegeben durch
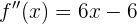
Der Wendepunkt ist gefunden, wenn  . Das heißt
. Das heißt

 ist somit der Wendepunkt.
ist somit der Wendepunkt.
Der Wert der Ableitung am Wendepunkt ist:
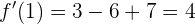
Die Steigung von  für
für  ist also 4. Die Tangente muss diese Steigung haben.
ist also 4. Die Tangente muss diese Steigung haben.
Wenn wir die Funktion für  auswerten, erhalten wir:
auswerten, erhalten wir:
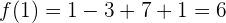
Daher verläuft die Funktion durch den Punkt 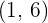 und die Tangente muss durch denselben Punkt verlaufen.
und die Tangente muss durch denselben Punkt verlaufen.
1 Um die Gleichung der Tangente bestimmen zu können, verwenden wir die Punkt-Steigungs-Formel mit  und
und 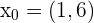 :
:
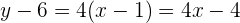
Die Gleichung der Tangente ist also
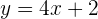
2 Um nun die Gleichung der Geraden zu bestimmen, gehen wir ganz ähnlich vor, nun aber mit 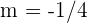 und
und 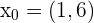 :
:
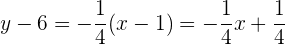
Die Gleichung der Geraden ist also
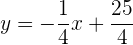
oder
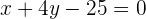
Die Menge  drückt das Geld aus, das sich während eines Tages in einem Spielautomaten angesammelt hat, und wird wie folgt berechnet:
drückt das Geld aus, das sich während eines Tages in einem Spielautomaten angesammelt hat, und wird wie folgt berechnet:
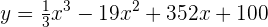 ,
,
wobei die Variable  die Zeit in Stunden ausdrückt (zwischen 0 und 24). Beantworte folgende Fragen:
die Zeit in Stunden ausdrückt (zwischen 0 und 24). Beantworte folgende Fragen:
a Geht dem Automaten jemals das Geld aus?
b Wenn die "Abrechnung" nach 24 Stunden erfolgt, macht der Automat dann einen Gewinn für die Besitzer des Automaten?
c Zu welchem Zeitpunkt ist der Geldbetrag am höchsten und zu welchem Zeitpunkt am niedrigsten?
d Zu welchem Zeitpunkt zahlt der Automat den höchsten Gewinn aus?
a Geht dem Automaten jemals das Geld aus?
Um diese Frage zu beantworten, müssen wir verifizieren, dass 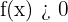 für alle
für alle 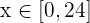 . Das ist gar nicht so einfach, da wir die Nullstellen von
. Das ist gar nicht so einfach, da wir die Nullstellen von  bestimmen müssen und es sich um eine Gleichung 3. Grades handelt. Der einfachste Weg ist, die Funktion grafisch darzustellen:
bestimmen müssen und es sich um eine Gleichung 3. Grades handelt. Der einfachste Weg ist, die Funktion grafisch darzustellen:
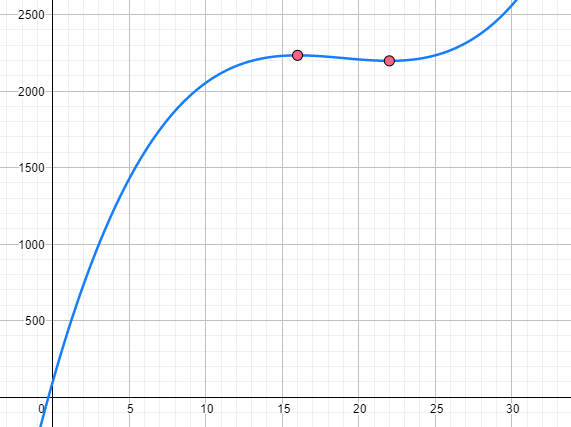
Wir stellen fest, dass der Graph im gesamten Intervall 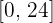 positiv ist. Wir sehen auch, dass der Graph sehr große Werte, sogar größere als
positiv ist. Wir sehen auch, dass der Graph sehr große Werte, sogar größere als 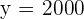 , annimmt.
, annimmt.
Daraus können wir schließen, dass dem Automaten nie die Münzen ausgehen.
b Die Abrechnung wird nach 24 Stunden gemacht. Erzielt die Maschine einen Gewinn für die Besitzer des Automaten?
Um diese Frage zu beantworten, müssen wir den Geldbetrag zu Beginn und am Ende des 24-Stunden-Zeitraums ermitteln. Also 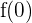 und
und 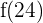 . Wir erhalten
. Wir erhalten
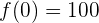
und
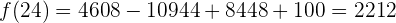
Nach 24 Stunden sind also 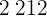 Euro im Automaten. Dies bedeutet einen Gewinn von
Euro im Automaten. Dies bedeutet einen Gewinn von 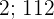 Euro pro Tag.
Euro pro Tag.
c Zu welchem Zeitpunkt ist der Geldbetrag am höchsten und zu welchem Zeitpunkt am niedrigsten?
Wir definieren die Zeitpunkte der höchsten und niedrigsten Einnahmen als die Momente, in denen das meiste bzw. das wenigste Geld im Automaten ist.
Aus der Abbildung geht hervor, dass der Automat am wenigsten Geld hat, wenn  ist, da dies der einzige Fall ist, in dem
ist, da dies der einzige Fall ist, in dem 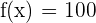 ist. Dieses Minimum kann nicht mit der Ableitung ermittelt werden.
ist. Dieses Minimum kann nicht mit der Ableitung ermittelt werden.
Für die höchste Einnahme müssen wir das Maximum der Funktion bestimmen. Wir müssen also ableiten:
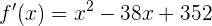
Wir ermitteln die Nullstellen wie folgt:
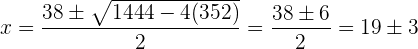
Die Nullstellen sind also 16 und 22.
Wir berechnen die 2. Ableitung:
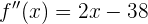
und stellen fest, dass 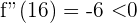 . Ein Maximum befindet sich somit bei
. Ein Maximum befindet sich somit bei  . Bei der Auswertung von
. Bei der Auswertung von 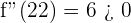 ist
ist  ein lokales Minimum (dessen Wert jedoch größer ist als der von
ein lokales Minimum (dessen Wert jedoch größer ist als der von 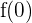 .
.
Bevor wir zu dem Schluss kommen, dass der Zeitpunkt des maximalen Ertrags  ist, müssen wir prüfen, ob
ist, müssen wir prüfen, ob 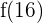 größer ist als
größer ist als 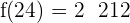 :
:
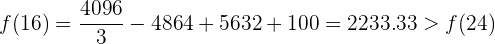
Der Zeitpunkt des höchsten Betrags ist also, wenn  . Das heißt in Stunde 16.
. Das heißt in Stunde 16.
d Zu welchem Zeitpunkt zahlt der Automat den höchsten Gewinn aus?
Der höchste Gewinn wird ausgezahlt, wenn  so stark wie möglich fällt. Die Funktion fällt nur zwischen 16 und 22, sodass zu einem dieser Zeitpunkte der höchste Gewinn ausgezahlt wird. Dies kann auf zwei Arten ermittelt werden. Eine Möglichkeit besteht darin, das Minimum von
so stark wie möglich fällt. Die Funktion fällt nur zwischen 16 und 22, sodass zu einem dieser Zeitpunkte der höchste Gewinn ausgezahlt wird. Dies kann auf zwei Arten ermittelt werden. Eine Möglichkeit besteht darin, das Minimum von  zu bestimmen, das, da es sich um eine Parabel handelt, der Mittelpunkt ihrer Nullstellen (16 und 22) ist, also 19.
zu bestimmen, das, da es sich um eine Parabel handelt, der Mittelpunkt ihrer Nullstellen (16 und 22) ist, also 19.
Eine andere Möglichkeit besteht darin, den Wendepunkt mithilfe der 2. Ableitung zu ermitteln. In diesem Fall 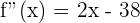 . Wenn wir gleich 0 setzen, erhalten wir
. Wenn wir gleich 0 setzen, erhalten wir

und somit 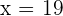 . Genau wie wir es vorher berechnet hatten. Folglich wird in Stunde 19 der höchste Gewinn ausgezahlt.
. Genau wie wir es vorher berechnet hatten. Folglich wird in Stunde 19 der höchste Gewinn ausgezahlt.
Gegeben ist 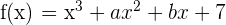 . Ermittle die Werte für
. Ermittle die Werte für  und
und  , sodass der Graph der Funktion
, sodass der Graph der Funktion  einen Wendepunkt bei
einen Wendepunkt bei  hat und seine Tangente an diesem Punkt einen Winkel von
hat und seine Tangente an diesem Punkt einen Winkel von 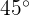 mit der x-Achse bildet.
mit der x-Achse bildet.
Um den Wendepunkt zu bestimmen, benötigen wir die 2. Ableitung. Daher beginnen wir mit der Berechnung der 1. Ableitung:
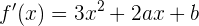
Die 2. Ableitung ist

Da wir möchten, dass sich der Wendepunkt bei  befindet, gehen wir wie folgt vor:
befindet, gehen wir wie folgt vor:
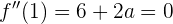
Wir erhalten die Gleichung 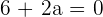 und somit
und somit  . Außerdem soll die Tangente an diesem Punkt einen Winkel von
. Außerdem soll die Tangente an diesem Punkt einen Winkel von 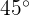 mit der x-Achse bilden. Wir wissen, dass der Tangens dieses Winkels die Steigung ist und somit
mit der x-Achse bilden. Wir wissen, dass der Tangens dieses Winkels die Steigung ist und somit

Die Tangente muss eine Steigung von 1 haben muss, das heißt 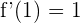 . Wir erhalten
. Wir erhalten
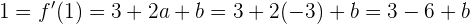
Daraus folgt, dass 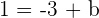 oder
oder  .
.
Deshalb ist  und
und  .
.
Bestimme die Gleichung der Tangente an den Graphen von 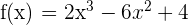 an seinem Wendepunkt.
an seinem Wendepunkt.
Zunächst müssen wir den Wendepunkt ermitteln. Dazu muss die 2. Ableitung gleich null sein. Wir berechnen zuerst die 1. Ableitung:
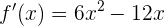
Die 2. Ableitung ist also
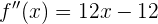
Wenn wir also gleich 0 setzen, erhalten wir 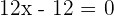 oder
oder  . Der Wendepunkt liegt also bei
. Der Wendepunkt liegt also bei  . Nun werten wir
. Nun werten wir  für
für  aus:
aus:
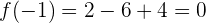 ,
,
sodass der Wendepunkt der Punkt  ist.
ist.
Die Steigung der Tangente ist 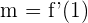 . Wir werten
. Wir werten  also für
also für  aus:
aus:
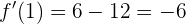
Damit können wir nun die Gleichung der Tangente mit Hilfe der Punkt-Steigungs-Formel ermitteln:
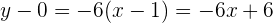
Die Gleichung der Tangente ist somit

Bestimme  ,
,  und
und  , sodass die Funktion
, sodass die Funktion 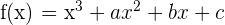 ein Maximum bei
ein Maximum bei 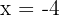 und ein Minimum bei
und ein Minimum bei  hat und den Wert 1 bei
hat und den Wert 1 bei  annimmt.
annimmt.
Da wir bereits wissen, wo sich die Maxima und Minima befinden, benötigen wir die 1. Ableitung der Funktion:
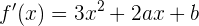 ,
,
wobei die kritischen Werte bei 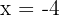 und
und  liegen müssen (beachte, dass es keine Rolle spielt, ob es sich um Minima oder Maxima handelt, da der Leitkoeffizient 1 ist und sich das Maximum immer auf der linken Seite befindet). Es muss also gelten, dass
liegen müssen (beachte, dass es keine Rolle spielt, ob es sich um Minima oder Maxima handelt, da der Leitkoeffizient 1 ist und sich das Maximum immer auf der linken Seite befindet). Es muss also gelten, dass 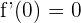 und
und 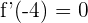 :
:
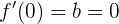
Daraus folgt, dass  sowie
sowie
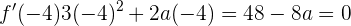
Wir erhalten  , wenn wir
, wenn wir  bestimmen.
bestimmen.
Und schließlich wissen wir, dass 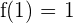 . Somit:
. Somit:
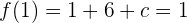
Wir erhalten 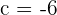 . Die Werte sind also
. Die Werte sind also
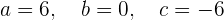
und die Funktion ist 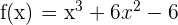 .
.
Bestimme  ,
,  ,
,  ,
,  und
und  , sodass der Graph
, sodass der Graph 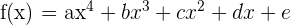 einen kritischen Punkt bei
einen kritischen Punkt bei  sowie einen Wendepunkt, der die Gerade
sowie einen Wendepunkt, der die Gerade  tangiert, am Punkt
tangiert, am Punkt  hat.
hat.
Wir wissen, dass  einen Wendepunkt bei
einen Wendepunkt bei  hat. Das bedeutet:
hat. Das bedeutet:
1  muss durch den Punkt
muss durch den Punkt  verlaufen:
verlaufen:

Deshalb ist 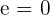 .
.
2 Die 2. Ableitung von  muss 0 sein bei
muss 0 sein bei  . Wir berechnen also die Ableitungen:
. Wir berechnen also die Ableitungen:
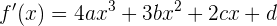
und
 ,
,
wobei erfüllt sein muss, dass 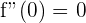 :
:
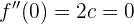
Daraus folgt, dass 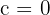 .
.
Wir müssen nun noch die Konstanten  ,
,  und
und  bestimmen. Wir wissen jedoch bereits, dass die Funktion folgende Form hat
bestimmen. Wir wissen jedoch bereits, dass die Funktion folgende Form hat
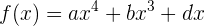
Wir wissen, dass die Funktion  (Steigung 2) am Punkt
(Steigung 2) am Punkt  tangiert. Daraus folgt, dass
tangiert. Daraus folgt, dass 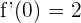 sein muss:
sein muss:
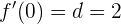
Wir erhalten also  .
.
Wir wissen außerdem, dass  einen kritischen Punkt bei
einen kritischen Punkt bei  hat. Dies bedeutet, dass
hat. Dies bedeutet, dass
1  durch den Punkt
durch den Punkt  verläuft, oder dass
verläuft, oder dass 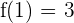 . Somit:
. Somit:
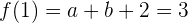
oder

2 Die Ableitung von  für
für  muss 0 sein. Das heißt:
muss 0 sein. Das heißt:
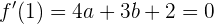
oder
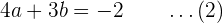
Wir stellen fest, dass (1) und (2) ein Gleichungssystem bilden. Eine Möglichkeit, dieses zu lösen, besteht darin, (1) mit 3 zu multiplizieren und das Ergebnis von (2) zu subtrahieren. Wir erhalten:
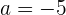
Im Anschluss setzen wir diesen Wert in (1) ein, um  oder
oder  zu erhalten.
zu erhalten.
Somit
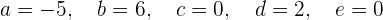
Der Graph 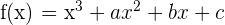 schneidet die x-Achse bei
schneidet die x-Achse bei  und hat einen Wendepunkt bei
und hat einen Wendepunkt bei 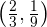 . Bestimmte die Werte für
. Bestimmte die Werte für  ,
,  und
und  .
.
Da der Graph die x-Achse bei  schneidet, muss
schneidet, muss  sein. Das heißt
sein. Das heißt
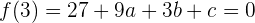
oder

Uns ist außerdem ein Wendepunkt von  bekannt. Dies bedeutet zwei Dinge:
bekannt. Dies bedeutet zwei Dinge:
1  muss durch den Punkt
muss durch den Punkt 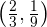 verlaufen
verlaufen

das heißt
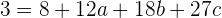
oder

2 Außerdem wissen wir, dass der Wendepunkt bei 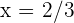 liegt. Wir benötigen also die 2. Ableitung von
liegt. Wir benötigen also die 2. Ableitung von  und berechnen zunächst die 1. Ableitung:
und berechnen zunächst die 1. Ableitung:
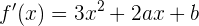
Die 2. Ableitung ist

Hieraus folgt, dass 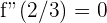 . Das heißt
. Das heißt
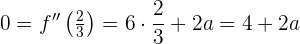
Und schließlich  .
.
Wir setzen nun  in die beiden vorherigen Gleichungen ein. Wenn wir in Gleichung (2) einsetzen, erhalten wir
in die beiden vorherigen Gleichungen ein. Wenn wir in Gleichung (2) einsetzen, erhalten wir  . Das heißt
. Das heißt
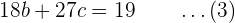
und wenn wir in Gleichung (1) einsetzen, erhalten wir 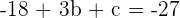 . Das heißt
. Das heißt

Wenn wir in Gleichung (3) einsetzen, erhalten wir
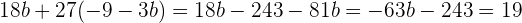
Das heißt 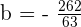 . Wenn wir dann in den Ausdruck für
. Wenn wir dann in den Ausdruck für  einsetzen, erhalten wir
einsetzen, erhalten wir
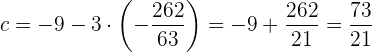
Die Werte sind also
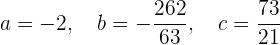
Gegeben ist die Funktion
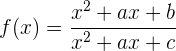
ermittle die Werte für  ,
,  und
und  , sodass die Funktion
, sodass die Funktion  bei
bei  einen lokalen Extrempunkt hat und der Graph durch den Koordinatenursprung verläuft.
einen lokalen Extrempunkt hat und der Graph durch den Koordinatenursprung verläuft.
Wir möchten, dass der Graph durch den Koordinatenursprung verläuft. Das heißt  . Wenn wir die Funktion im Ursprung auswerten, erhalten wir:
. Wenn wir die Funktion im Ursprung auswerten, erhalten wir:
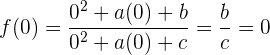
Daraus folgt, dass  sowie
sowie  . Wir haben also bereits einen der drei Werte gefunden.
. Wir haben also bereits einen der drei Werte gefunden.
Außerdem wissen wir, dass  einen lokalen Extrempunkt bei
einen lokalen Extrempunkt bei  haben muss. Dies bedeutet zwei Dinge:
haben muss. Dies bedeutet zwei Dinge:
1 Erstens: 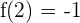 . Das heißt, dass
. Das heißt, dass  durch den Punkt
durch den Punkt  verlaufen muss. Wenn wir also
verlaufen muss. Wenn wir also  für 2 auswerten, erhalten wir
für 2 auswerten, erhalten wir

Wir bringen den Nenner durch Multiplikation auf die andere Seite und erhalten
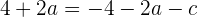
das heißt

2 Außer dass  durch
durch  verlaufen muss, muss auch gelten, dass
verlaufen muss, muss auch gelten, dass 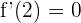 , damit die Funktion einen lokalen Extrempunkt an diesem Punkt hat. Deshalb müssen wir die Ableitung von
, damit die Funktion einen lokalen Extrempunkt an diesem Punkt hat. Deshalb müssen wir die Ableitung von  mithilfe der Quotientenregel bestimmen:
mithilfe der Quotientenregel bestimmen:
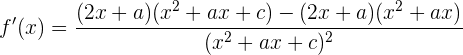
Wir vereinfachen und erhalten

Wir werten für die Zahl 2 aus und erhalten:
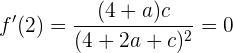
Es muss gelten, dass 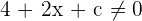 , damit die Ableitung definiert ist. Der Ausdruck ist also äquivalent zu
, damit die Ableitung definiert ist. Der Ausdruck ist also äquivalent zu 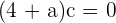 . Da wir wissen, dass
. Da wir wissen, dass  , muss
, muss 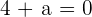 sein. Somit ist
sein. Somit ist 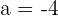 .
.
Setzen wir dann die Gleichung des vorherigen Falls ein, erhalten wir:
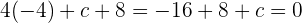
das heißt 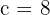 .
.
Unsere Ergebnisse sind 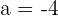 ,
, 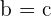 und
und 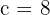 .
.
Bestimme die Werte von  und
und  , sodass die Funktion
, sodass die Funktion 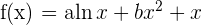 Extremstellen an den Punkten
Extremstellen an den Punkten 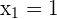 und
und  hat. Angesichts dieser Werte von
hat. Angesichts dieser Werte von  und
und  , welche Art von Extremstellen hat die Funktion bei
, welche Art von Extremstellen hat die Funktion bei  und
und  ?
?
Da die Funktion Extremstellen für 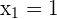 und
und  haben soll, müssen
haben soll, müssen  und
und 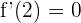 sein.
sein.
Deshalb berechnen wir zunächst die Ableitung der Funktion
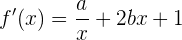
Nun werten wir für 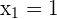 aus:
aus:
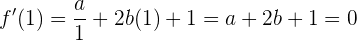
Und wir werten für  aus:
aus:
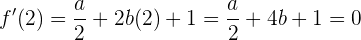
Daraus ergibt sich folgendes Gleichungssystem
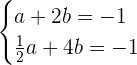
Die Lösung ist  und
und  . Deshalb sind die Werte
. Deshalb sind die Werte

und unsere Funktion ist
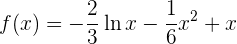
Um festzustellen, ob es sich um Minima oder Maxima handelt, berechnen wir dann die 2. Ableitung:

Wir werten für 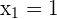 aus:
aus:
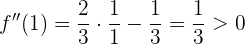
und erhalten ein Minimum für 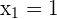 . Ähnlich verhält es sich, wenn wir für
. Ähnlich verhält es sich, wenn wir für  auswerten:
auswerten:
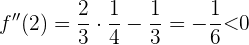
Wir erhalten ein Maximum für  .
.
Mit KI zusammenfassen:


