Kapitel

Erste Ableitung
Die Ableitung ist ein Grenzwert, gegen der Quotient aus der Zunahme einer Funktion und der willkürlichen Zunahme der unabhängigen Variablen konvergiert, wenn letztere gegen 0 konvergiert.
Ein reales Beispiel für die Ableitung ist ein nach oben geworfener Ball, dessen Höhenänderung durch 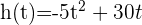 gegeben ist. Durch die Ableitung kann man ermitteln, wie hoch die Geschwindigkeit zu einem bestimmten Zeitpunkt ist.
gegeben ist. Durch die Ableitung kann man ermitteln, wie hoch die Geschwindigkeit zu einem bestimmten Zeitpunkt ist.
Wenn wir eine Funktion  ableiten, erhalten wir die 1. Ableitung
ableiten, erhalten wir die 1. Ableitung  .
.
Wenn wir wieder ableiten, erhalten wir eine neue Funktion, die 2. Ableitung 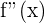 .
.
Und wenn wir nochmals ableiten, erhalten wir die 3. Ableitung 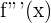 .
.
Wenn wir erneut ableiten, erhalten wir die 4. Ableitung 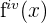 usw.
usw.
Formeln für Ableitungen
Ableitung einer Konstante.
1 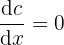 .
.
Ableitung von  .
.
2 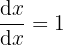 .
.
Ableitung eines Produkts aus Konstante und Variable.
3 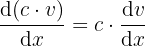 .
.
Ableitung einer Summe und Differenz von Variablen.
4 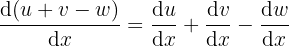 .
.
Ableitung von  zu einer Potenz.
zu einer Potenz.
5 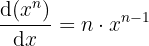 .
.
Ableitung der Multiplikation von zwei Variablen.
6 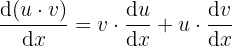 .
.
Ableitung einer rationalen Funktion.
7 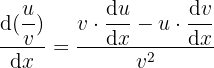 .
.
Ableitung der Sinusfunktion.
8 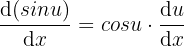 .
.
Ableitung der Kosinusfunktion.
9 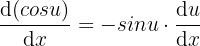 .
.
Ableitung der Logarithmusfunktion.
10 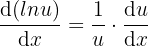 .
.
Ableitung der Exponentialfunktion.
11 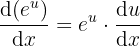 .
.
Beispiel für die 1. Ableitung
1 Berechne die 1. Ableitung der Funktion 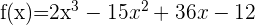 .
.
Da es sich um ein Polynom handelt, leiten wir Term für Term ab
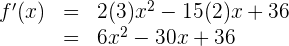
2 Berechne die 1. Ableitung der Funktion  .
.
Da es sich um ein Polynom handelt, leiten wir Term für Term ab
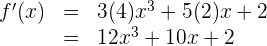
Ejemplo de la segunda derivada
1 Berechne die 2. Ableitung der Funktion 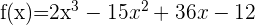 .
.
Im obigen Beispiel berechneten wir die 1. Ableitung 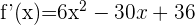 .
.
Da es sich um ein Polynom handelt, leiten wir Term für Term ab
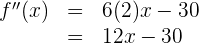
2 Berechne die 2. Ableitung der Funktion  .
.
Im obigen Beispiel berechneten wir die 1. Ableitung 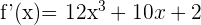 .
.
Da es sich um ein Polynom handelt, leiten wir Term für Term ab
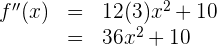
Ejemplo de la tercera derivada
1 Berechne die 3. Ableitung der Funktion 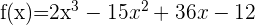 .
.
Im obigen Beispiel berechneten wir die 2. Ableitung  .
.
Da es sich um ein Polynom handelt, leiten wir Term für Term ab
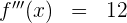
2 Berechne die 3. Ableitung der Funktion  .
.
Im obigen Beispiel berechneten wir die 2. Ableitung 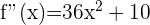 .
.
Da es sich um ein Polynom handelt, leiten wir Term für Term ab
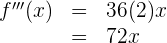
Beispiel für die 4. Ableitung
1 Berechne die 4. Ableitung der Funktion 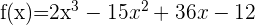 .
.
Im obigen Beispiel berechneten wir die 3. Ableitung 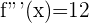 .
.
Da es sich um eine Konstante handelt, bleibt
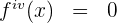
2 Berechne die 4. Ableitung der Funktion  .
.
Im obigen Beispiel berechneten wir die 3. Ableitung 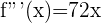 .
.
Da es sich um ein Polynom handelt, leiten wir Term für Term ab
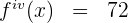
Beispiel für die 5. Ableitung
1 Berechne die 5. Ableitung der Funktion  .
.
Im obigen Beispiel berechneten wir die 4. Ableitung  .
.
Da es sich um ein Polynom handelt, leiten wir Term für Term ab
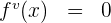
n-te Ableitung
In einigen Fällen können wir eine allgemeine Formel für jede (und alle) der aufeinanderfolgenden Ableitungen finden. Diese Formel ist die n-te Ableitung f'n(x).
Beispiel für die n-te Ableitung einer rationalen Funktion
Berechne die n-te Ableitung der Funktion 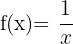 .
.
Wir berechnen die 1. Ableitung
Da es sich um eine rationale Funktion handelt,
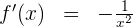
Wir berechnen die 2. Ableitung
Da es sich um eine rationale Funktion handelt,
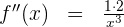
Wir berechnen die 3. Ableitung
Da es sich um eine rationale Funktion handelt,
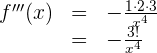
Da es sich um eine rationale Funktion handelt, vereinfachen wir und erhalten die n-te Ableitung
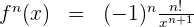
Beispiel für die n-te Ableitung einer Logarithmusfunktion
Berechne die n-te Ableitung der Funktion 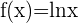 .
.
Wir berechnen die 1. Ableitung
Da es sich um eine Logarithmusfunktion handelt,
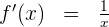
Wir berechnen die 2. Ableitung
Da es sich um eine rationale Funktion handelt,
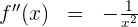
Wir berechnen die 3. Ableitung
Da es sich um eine rationale Funktion handelt,
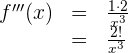
Wir berechnen die 4. Ableitung
Da es sich um eine rationale Funktion handelt,
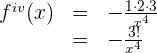
Da es sich um eine rationale Funktion handelt, vereinfachen wir und erhalten die n-te Ableitung
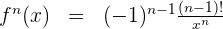
Beispiel für die n-te Ableitung einer trigonometrischen Funktion
Berechne die n-te Ableitung der Funktion 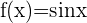 .
.
Wir berechnen die 1. Ableitung
Da es sich um eine trigonometrische Funktion handelt, wenden wir die entsprechenden Formeln an
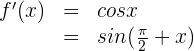
Wir berechnen die 2. Ableitung
Da es sich um eine trigonometrische Funktion handelt, wenden wir die entsprechenden Formeln an
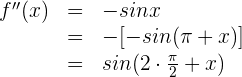
Wir berechnen die 3. Ableitung
Da es sich um eine trigonometrische Funktion handelt, wenden wir die entsprechenden Formeln an
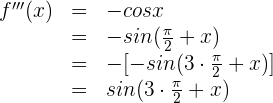
Da es sich um eine trigonometrische Funktion handelt, vereinfachen wir und erhalten die n-te Ableitung
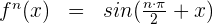
Beispiel für die n-te Ableitung einer Exponentialfunktion
Berechne die n-te Ableitung der Funktion 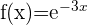 .
.
Wir berechnen die 1. Ableitung
Da es sich um eine Exponentialfunktion handelt,
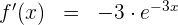
Wir berechnen die 2. Ableitung
Da es sich um eine Exponentialfunktion handelt,
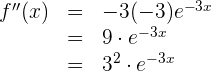
Wir berechnen die 3. Ableitung
Da es sich um eine Exponentialfunktion handelt,
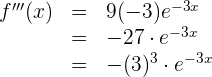
Da es sich um eine Exponentialfunktion handelt, vereinfachen wir und erhalten die n-te Ableitung
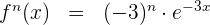
Mit KI zusammenfassen:












