Untersuche die Stetigkeit und die Ableitbarkeit der Funktion 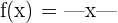 .
.
Untersuche die Stetigkeit und die Ableitbarkeit der Funktion 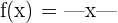 .
.
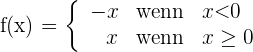
1 Zunächst untersuchen wir die Stetigkeit bei 

Die Funktion ist stetig.
2 Wir untersuchen die Ableitbarkeit.
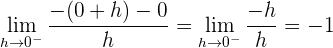
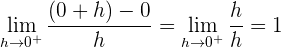
Da die seitlichen Ableitungen bei  unterschiedlich sind, ist die Funktion an diesem Punkt nicht ableitbar.
unterschiedlich sind, ist die Funktion an diesem Punkt nicht ableitbar.
Untersuche die Stetigkeit und die Ableitbarkeit der Funktion
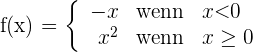
Untersuche die Stetigkeit und die Ableitbarkeit der Funktion
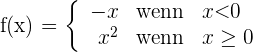
1 Zunächst untersuchen wir die Stetigkeit bei 

Die Funktion ist stetig.
2 Wir untersuchen die Ableitbarkeit.
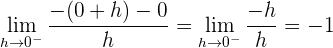
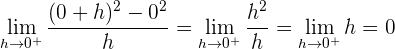
Da die seitlichen Ableitungen bei  unterschiedlich sind, ist die Funktion an diesem Punkt nicht ableitbar.
unterschiedlich sind, ist die Funktion an diesem Punkt nicht ableitbar.
Untersuche die Stetigkeit und die Ableitbarkeit der Funktion
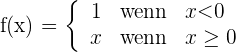
Untersuche die Stetigkeit und die Ableitbarkeit der Funktion
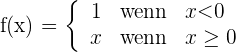
1 Zunächst untersuchen wir die Stetigkeit bei 

Die Funktion ist nicht stetig und somit auch nicht ableitbar.
Untersuche die Stetigkeit und die Ableitbarkeit der Funktion
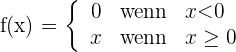
Untersuche die Stetigkeit und die Ableitbarkeit der Funktion
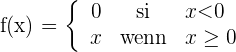
1 Zunächst untersuchen wir die Stetigkeit bei 
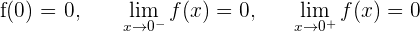
Die Funktion ist stetig.
2 Wir untersuchen die Ableitbarkeit.
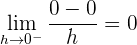
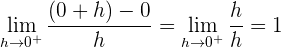
Da die seitlichen Ableitungen bei  unterschiedlich sind, ist die Funktion an diesem Punkt nicht ableitbar.
unterschiedlich sind, ist die Funktion an diesem Punkt nicht ableitbar.
Ermittle den Punkt, an dem 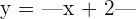 keine Ableitung hat. Begründe das Ergebnis, indem du es grafisch darstellst.
keine Ableitung hat. Begründe das Ergebnis, indem du es grafisch darstellst.
Ermittle den Punkt, an dem 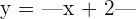 keine Ableitung hat. Begründe das Ergebnis, indem du es grafisch darstellst.
keine Ableitung hat. Begründe das Ergebnis, indem du es grafisch darstellst.
1 Wir wandeln in eine abschnittsweise definierte Funktion um
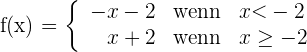
2 Wir untersuchen die Stetigkeit bei 
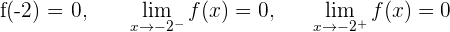
Die Funktion ist im gesamten Bereich  stetig.
stetig.
3 Wir untersuchen die Ableitbarkeit.
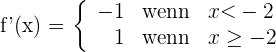
Da die seitlichen Ableitungen bei 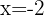 unterschiedlich sind, ist die Funktion an diesem Punkt nicht ableitbar.
unterschiedlich sind, ist die Funktion an diesem Punkt nicht ableitbar.
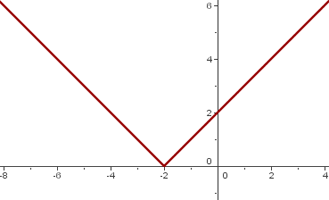
Bei 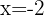 gibt es eine Spitze, sodass sie an diesem Punkt nicht ableitbar ist.
gibt es eine Spitze, sodass sie an diesem Punkt nicht ableitbar ist.
Ermittle die Punkte, an denen 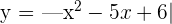 keine Ableitung hat. Begründe das Ergebnis durch Darstellung des Graphen.
keine Ableitung hat. Begründe das Ergebnis durch Darstellung des Graphen.
Ermittle die Punkte, an denen 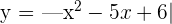 keine Ableitung hat. Begründe das Ergebnis durch Darstellung des Graphen.
keine Ableitung hat. Begründe das Ergebnis durch Darstellung des Graphen.
1 Wir wandeln in eine abschnittsweise definierte Funktion um
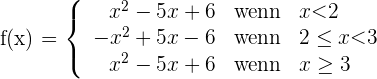
2 Wir untersuchen die Stetigkeit bei  und
und 

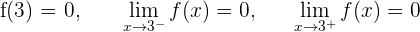
Die Funktion ist im gesamten Bereich  stetig.
stetig.
3 Wir untersuchen die Ableitbarkeit.
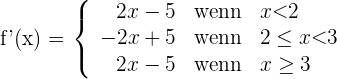
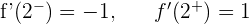
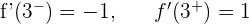
Da die seitlichen Ableitungen bei  und
und  unterschiedlich sind, ist die Funktion an diesen Punkten nicht ableitbar.
unterschiedlich sind, ist die Funktion an diesen Punkten nicht ableitbar.
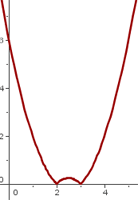
Wir sehen, dass wir bei x = 2 und x = 3 zwei Winkelpunkte haben, sodass die Funktion an diesen Punkten nicht ableitbar ist.
Untersuche die Stetigkeit und Ableitbarkeit der wie folgt definierten Funktion:
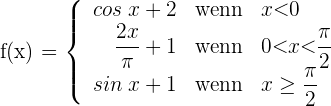
Untersuche die Stetigkeit und Ableitbarkeit der wie folgt definierten Funktion:
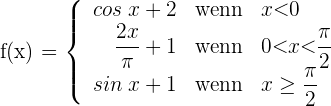
1 Die Funktion ist bei  nicht stetig, da sie keine Abbildung besitzt. Sie kann deshalb auch nicht abgeleitet werden. Wir untersuchen die Stetigkeit bei
nicht stetig, da sie keine Abbildung besitzt. Sie kann deshalb auch nicht abgeleitet werden. Wir untersuchen die Stetigkeit bei 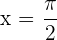
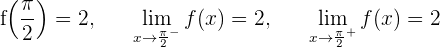
Die Funktion ist bei 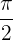 stetig.
stetig.
2 Wir untersuchen die Ableitbarkeit.
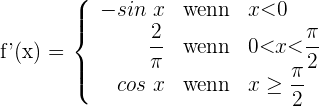
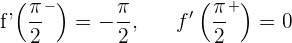
Da die seitlichen Ableitungen unterschiedlich sind, ist die Funktion bei 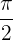 nicht ableitbar.
nicht ableitbar.
Gegeben ist die Funktion:
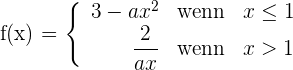
Für welche Werte von  ist sie ableitbar?
ist sie ableitbar?
Gegeben ist die Funktion:
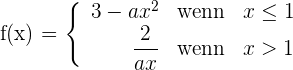
Für welche Werte von  kann sie abgeleitet werden?
kann sie abgeleitet werden?
1 Wir untersuchen die Stetigkeit bei 

Damit die Funktion bei  stetig ist, müssen die seitlichen Grenzwerte gleich sein
stetig ist, müssen die seitlichen Grenzwerte gleich sein

2 Wir untersuchen die Ableitbarkeit bei 
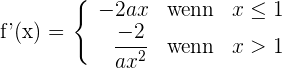
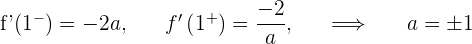
Ableitbar für 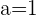 . Für
. Für 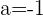 ist die Funktion nicht stetig.
ist die Funktion nicht stetig.
Untersuche, für welche Werte von  und
und  die Funktion stetig und ableitbar ist:
die Funktion stetig und ableitbar ist:
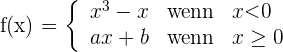
Untersuche, für welche Werte von  und
und  die Funktion stetig und ableitbar ist:
die Funktion stetig und ableitbar ist:
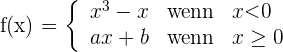
1 Wir untersuchen die Stetigkeit bei 

Damit die Funktion bei  stetig ist, müssen die seitlichen Grenzwerte gleich sein, also
stetig ist, müssen die seitlichen Grenzwerte gleich sein, also 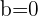
2 Wir untersuchen die Ableitbarkeit bei 
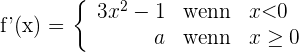
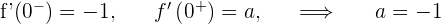
Ableitbar für 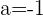 .
.
Ermittle die Werte von  und
und  , für die die folgende Funktion an allen Punkten ableitbar ist:
, für die die folgende Funktion an allen Punkten ableitbar ist:
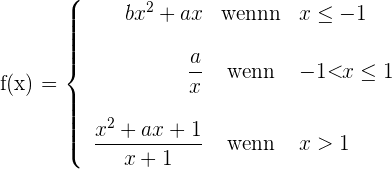
Ermittle die Werte von  und
und  , für die die folgende Funktion an allen Punkten ableitbar ist:
, für die die folgende Funktion an allen Punkten ableitbar ist:
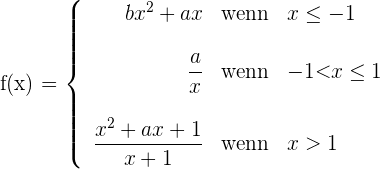
Damit eine Funktion an allen Punkten ableitbar ist, muss sie an allen Punkten stetig sein. In diesem Fall ist die Funktion bei  nicht stetig, da sie keine Abbildung hat. Die Funktion ist an diesem Punkt nicht definiert, das Ergebnis von
nicht stetig, da sie keine Abbildung hat. Die Funktion ist an diesem Punkt nicht definiert, das Ergebnis von  ist keine reelle Zahl.
ist keine reelle Zahl.
Für  und
und  existieren keine Werte, für die die Funktion stetig ist.
existieren keine Werte, für die die Funktion stetig ist.
Es gibt also keine Werte von  und
und  , für die die Funktion ableitbar ist.
, für die die Funktion ableitbar ist.
Untersuche, für welche Werte von  und
und  die Funktion stetig und ableitbar ist:
die Funktion stetig und ableitbar ist:
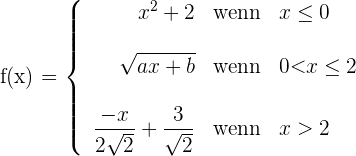
Untersuche, für welche Werte von  und
und  die Funktion stetig und ableitbar ist:
die Funktion stetig und ableitbar ist:
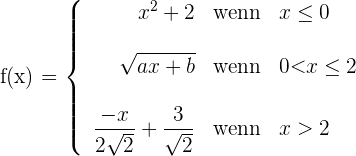
1 Wir untersuchen die Stetigkeit bei  und
und 
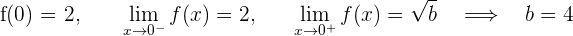
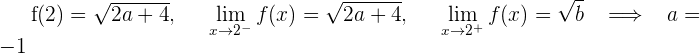
Damit die Funktion im gesamten Bereich  stetig ist, muss
stetig ist, muss 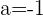 und
und 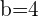 sein
sein
2 Wir untersuchen die Ableitbarkeit bei  und
und 
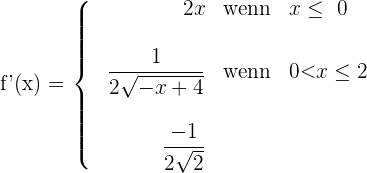
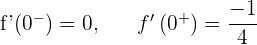
Sie ist nicht ableitbar bei  .
.
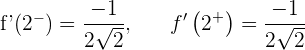
Sie ist ableitbar bei  .
.
Mit KI zusammenfassen:


