Die Ableitung berechnen
Berechne die Ableitungen für die angegebenen Punkte:
-
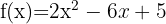 bei
bei 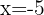 .
. -
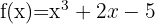 bei
bei  .
. -
 bei
bei  .
. -
 bei
bei  .
.
Es sei daran erinnert, dass eine Möglichkeit zur Berechnung der Ableitung in ihrer Definition besteht, d. h. in der Berechnung des folgenden Grenzwerts

1 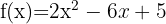 bei
bei 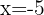
Die Ableitung berechnen

Wir eliminieren die Klammern und berechnen

Wir streichen Terme und faktorisieren  im Zähler
im Zähler

Wir vereinfachen und berechnen den Grenzwert
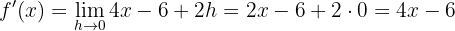
Und schließlich

Wir werten aus
Wir werten die Ableitung am Punkt 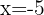 aus
aus
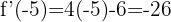
2 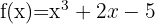 bei
bei  .
.
Die Ableitung berechnen
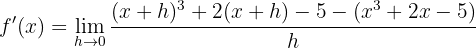
Wir eliminieren die Klammern und berechnen

Wir streichen Terme und faktorisieren  im Zähler
im Zähler

Wir vereinfachen und berechnen den Grenzwert

Schließlich

Auswerten
Wir werten die Ableitung am Punkt  aus
aus

3  bei
bei 
Die Ableitung berechnen
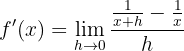
Wir berechnen

Wir vereinfachen und berechnen den Grenzwert

Auswerten
Wir werten die Ableitung am Punkt  aus
aus

4  bei
bei  .
.
Die Ableitung berechnen

Mutliplikation mit dem Konjugierten, um zu rationalisieren

Wir berechnen

Wir vereinfachen und berechnen den Grenzwert

Auswerten
Wir werten die Ableitung am Punkt  aus
aus

Wie hoch ist die Geschwindigkeit eines Fahrzeugs, das sich gemäß der Gleichung  in der fünften Sekunde seiner Fahrt bewegt? Die Strecke wird in Metern und die Zeit in Sekunden gemessen.
in der fünften Sekunde seiner Fahrt bewegt? Die Strecke wird in Metern und die Zeit in Sekunden gemessen.
Wir berechnen die Ableitung
Die Geschwindigkeit ist gleich der Ableitung der Gleichung der Position, in diesem Fall 
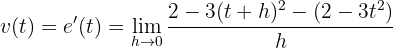
Wir eliminieren die Klammern und berechnen

Wir streichen Terme und faktorisieren  im Zähler
im Zähler

Wir vereinfachen und berechnen den Grenzwert

Auswerten

Bestimme die Koordinaten
Gegeben ist der Graph der Gleichung  . Bestimme die Koordinaten der Punkte auf diesem Graphen, an denen die Tangente einen Winkel von 45° mit der x-Achse bildet.
. Bestimme die Koordinaten der Punkte auf diesem Graphen, an denen die Tangente einen Winkel von 45° mit der x-Achse bildet.
Wir berechnen die Ableitung
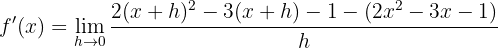
Wir eliminieren die Klammern und berechnen
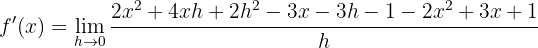
Wir streichen Terme und faktorisieren  im Zähler
im Zähler

Wir vereinfachen und berechnen den Grenzwert
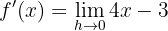
Wir setzen die Ableitung gleich und erhalten den Wert der Abszisse
Wir möchten, dass die Tangente an den Graphen einen Winkel von 45° mit der x-Achse bildet. Ihre Steigung muss also einen Wert von  haben
haben

Somit
4x-3=1 \hspace{2cm} 4x=4 \hspace{2cm} x=1
Die Ordinate erhalten und den Punkt ermitteln
Wir setzen den Punkt  in
in  ein und erhalten so die Ordinate des Punktes
ein und erhalten so die Ordinate des Punktes

Auf Stetigkeit und Ableitbarkeit untersuchen
Aufgrund der schlechten Umweltbedingungen beginnt eine Kolonie von einer Million Bakterien erst nach zwei Monaten mit der Vermehrung. Die Funktion, die die Population der Kolonie in Abhängigkeit von der Zeit (ausgedrückt in Monaten) darstellt, ist gegeben durch:
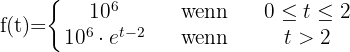
Folgendes wird verlangt:
-
Überprüfe, ob die Population eine stetige Funktion der Zeit ist.
-
Berechne die mittlere Änderungsrate der Population auf den Intervallen [0, 2] und [0, 4].
-
Berechne die momentane Änderungsrate bei t = 4.
1 Stetigkeit
Eine konstante Exponentialfunktion ist stetig, da  bei
bei  stetig ist.
stetig ist.
Es muss nur noch überprüft werden, ob  am Punkt
am Punkt  stetig ist
stetig ist
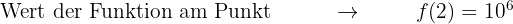


Da diese drei Werte gleich sind, ist die Funktion bei 2 stetig und somit in allen Punkten stetig.
2 Mittlere Änderungsrate bei [0, 2] und [0, 4]
[0, 2]
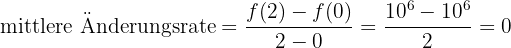
[0, 4]
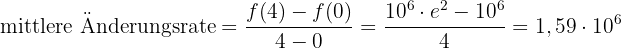
3 Momentane Änderungsrate bei t = 4
Die Ableitung ist durch folgende Funktion gegeben

Die Ableitung bei t=4 ist
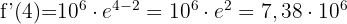
Die Ableitung der Exponentialfunktion wurde mit Hilfe der direkten Formel ermittelt.
Finde den Punkt, an dem  keine Ableitung hat. Begründe das Ergebnis, indem du es grafisch darstellst.
keine Ableitung hat. Begründe das Ergebnis, indem du es grafisch darstellst.
Die Funktion  ist äquivalent zu der folgenden Funktion
ist äquivalent zu der folgenden Funktion
überprüfen
Wir untersuchen die Stetigkeit bei 
Wir stellen fest, dass

Somit ist ist die Funktion stetig im gesamten Bereich 
Die Ableitung ist andererseits gegeben durch

Wir untersuchen die Ableitbarkeit bei 
Also sind der linksseitige und der rechtsseitige Grenzwert gegeben durch


Da sie nicht gleich sind, können wir daraus schließen, dass  nicht ableitbar ist bei:
nicht ableitbar ist bei:  .
.
Wir analysieren den Graphen
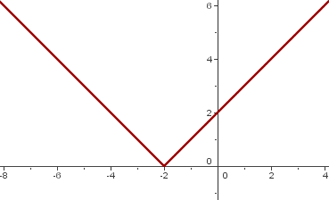
Bei  gibt es eine Spitze. Somit ist an diesem Punkt keine Ableitung möglich.
gibt es eine Spitze. Somit ist an diesem Punkt keine Ableitung möglich.
Finde die Punkte, an denen  keine Ableitung hat. Begründe das Ergebnis, indem du es grafisch darstellst.
keine Ableitung hat. Begründe das Ergebnis, indem du es grafisch darstellst.
Die Funktion  ist äquivalent zu der folgenden Funktion
ist äquivalent zu der folgenden Funktion
und  überprüfen
überprüfen
Wir untersuchen die Stetigkeit bei  y en
y en 
Wir stellen fest, dass
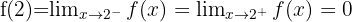

Somit ist ist die Funktion stetig im gesamten Bereich  .
.
Wir untersuchen die Ableitbarkeit bei  und
und 
Wir überprüfen die seitlichen Grenzwerte für 


Und die seitlichen Grenzwerte von  sind
sind


Da die seitlichen Ableitungen nicht übereinstimmen, kann die Funktion nicht abgeleitet werden bei:  und
und  .
.
Wir analysieren den Graphen
Wir sehen, dass wir bei  und
und  zwei winklige Punkte haben, so dass die Funktion dort nicht ableitbar ist.
zwei winklige Punkte haben, so dass die Funktion dort nicht ableitbar ist.
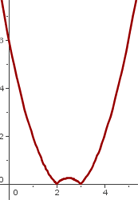
Untersuche die Stetigkeit und Ableitbarkeit der wie folgt definierten Funktion:
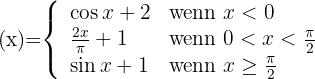
Die Funktion ist bei x = 0 nicht stetig, da sie keine Abbildung hat. Somit ist sie auch nicht ableitbar.
Wir untersuchen die Stetigkeit bei 
Der Wert in der Funktion lautet
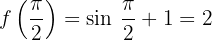
Die seitlichen Grenzwerte sind
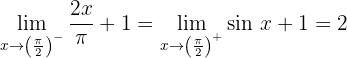
Da diese gleich sind, hat die Funktion an diesem Punkt einen Grenzwert und außerdem

Somit ist  stetig bei
stetig bei 
Wir möchten sehen, ob sie mit den Formeln der unmittelbaren trigonometrischen Ableitung ableitbar ist.
Wir berechnen die seitlichen Grenzwerte für 
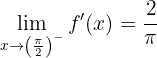

Da die seitlichen Ableitungen nicht übereinstimmen, ist die Ableitung an diesem Punkt nicht möglich.
Parameter bestimmen
Gegeben ist die Funktion:
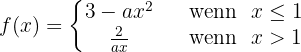
Für welche Werte von a ist sie ableitbar
Wir untersuchen die Stetigkeit bei 


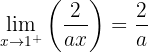
Damit sie stetig ist, müssen die seitlichen Grenzwerte gleich sein

Wir lösen die quadratische Gleichung

Wir untersuchen die Stetigkeit bei 
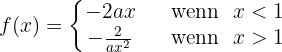
Die seitlichen Grenzwerte der Ableitung sind
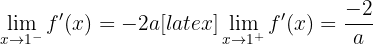
Damit sie ableitbar ist, müssen die seitlichen Grenzwerte gleich sein
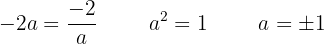
Um ableitbar zu sein, muss sie auch stetig sein, also ist sie nur für 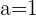 ableitbar, denn für
ableitbar, denn für 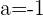 ist sie nicht stetig
ist sie nicht stetig
Untersuche, für welche Werte von a und b die Funktion stetig und ableitbar ist:
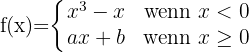
Wir untersuchen die Stetigkeit bei x = 0

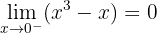

Damit sie stetig ist, müssen die seitlichen Grenzwerte gleich sein

Wir untersuchen die Ableitbarkeit bei x = 0
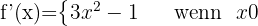


Damit sie ableitbar ist, müssen die seitlichen Grenzwerte gleich sein
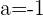
Bestimme die Werte von a und b, sodass die folgende Funktion an allen Punkten ableitbar ist:
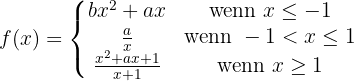
Damit eine Funktion an allen Punkten ableitbar ist, muss sie an allen Punkten stetig sein. In diesem Fall ist die Funktion bei x = 0 nicht stetig, da sie keine Abbildung hat. Die Funktion ist an diesem Punkt nicht definiert, das Ergebnis von a/0 ist keine reelle Zahl.
Es gibt keine Werte für a und b, durch die die Funktion stetig wird.
Daher gibt es keine Werte von a und b, für die die Funktion ableitbar ist.
Mit KI zusammenfassen:


