Kapitel
Wie wir wissen, können Ableitungen auf zwei Arten gelöst werden:
1. anhand des Grenzwerts mit der Formel
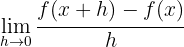
2. anhand konkreter Formeln für jeden einzelnen Fall.
In diesem Artikel lösen wir Ableitungsaufgaben über den zweiten Weg.

Berechne die Ableitungen der Funktionen
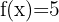
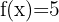
In diesem Fall verwenden wir die Formel 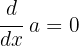 , die besagt, dass die Ableitung jeder beliebigen Konstante gleich Null ist.
, die besagt, dass die Ableitung jeder beliebigen Konstante gleich Null ist.



In diesem Fall verwenden wir die Formel  :
:
bei einer Variablen, die mit einer Konstante multipliziert wird, ist die Ableitung die Konstante.

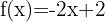
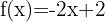
In diesem Fall verwenden wir die Regel 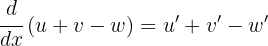 :
:
wenn eine Summe oder eine Differenz aus Funktionen (oder algebraischen Termen) vorliegt, ist die Ableitung gleich der Summe und/oder der Differenz der Ableitungen jeder einzelnen Funktion (oder jedes einzelnen algebraischen Terms).



In diesem Fall muss jeder algebraische Term abgeleitet werden.
Für den ersten verwenden wir die Formel 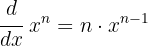 .
.



In diesem Fall muss jeder algebraische Term abgeleitet werden:
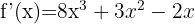
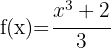
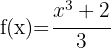
Hier kann die Funktion umgeschrieben werden:
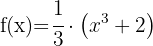
Die Ableitung ist also  mal die Ableitung der Funktion
mal die Ableitung der Funktion 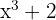
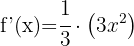

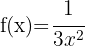
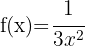
Bei dieser Art von Funktionen, bei denen die Variable im Nenner steht, können wir die Potenzregel anwenden:
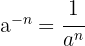
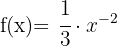
Für die Ableitung verwenden wir die Formel 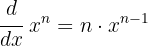
Wir erhalten:
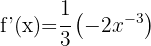



Um einen Quotienten abzuleiten, verwenden wir die Formel:

Als Ableitung erhalten wir:
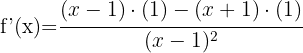

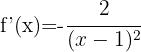


Um ein Produkt abzuleiten, verwenden wir die Formel:

Als Ableitung erhalten wir:
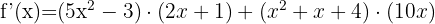
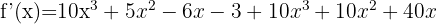
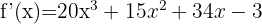
Berechne mit der Formel für Ableitungen von Potenzen
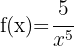
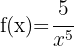
Wende die Potenzregeln an und schreibe die Funktion um:

Verwende die Formel für die Ableitung von Potenzen:
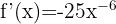
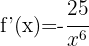
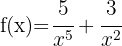
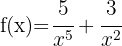
Wende die Potenzregeln an und schreibe die Funktion um:

Verwende die Formel für die Ableitung von Potenzen:
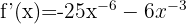



Wende die Potenzregeln an und schreibe die Funktion um:
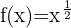
Verwende die Formel für die Ableitung von Potenzen:


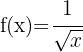
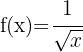
Wende die Potenzregeln an und schreibe die Funktion um:

Verwende die Formel für die Ableitung von Potenzen:
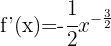
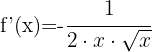


Wende die Potenzregeln an und schreibe die Funktion um:
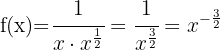
Verwende die Formel für die Ableitung von Potenzen:
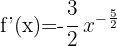
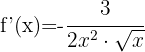
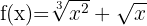
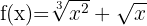
Wende die Potenzregeln an und schreibe die Funktion um:
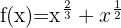
Verwende die Formel für die Ableitung von Potenzen:
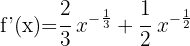
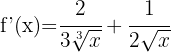
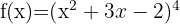
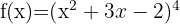
In diesem Beispiel liegt eine Funktion mit einem Exponenten vor. Wende daher die folgende Formel an:
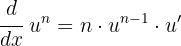

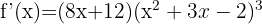
Berechne mit der Formel für Ableitungen von Wurzeln
Berechne mit der Formel für Ableitungen von Potenzen
Um Funktionen abzuleiten, die eine Wurzel enthalten, können wir sie zuerst in Potenzen umwandeln (wie in der vorherigen Aufgabe) oder die folgenden Formeln für die Ableitung verwenden:
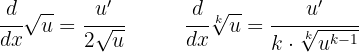


Da eine Quadratwurzel vorliegt, können wir die erste Formel verwenden:
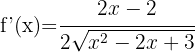
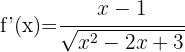


Da der Wurzelexponent 4 ist, verwenden wir die zweite Formel

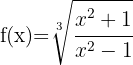
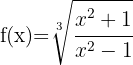
Da der Wurzelexponent 3 ist, verwenden wir die zweite Formel.
Die Funktion innerhalb der Wurzel kann anhand der Quotientenregel abgeleitet werden:

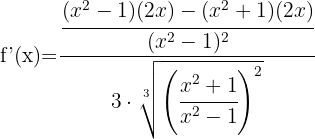
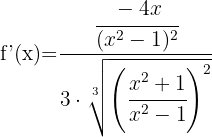
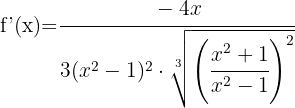
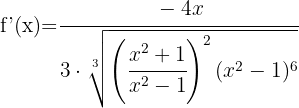
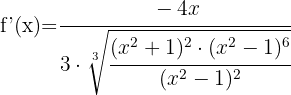
Wir vereinfachen den Ausdruck 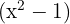 in Zähler und Nenner der Wurzel und lösen so den Nenner auf. Wir erhalten:
in Zähler und Nenner der Wurzel und lösen so den Nenner auf. Wir erhalten:
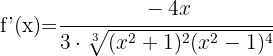

Leite die Exponentialfunktionen ab
Leite die Exponentialfunktionen ab
In dieser Aufgabe werden wir die folgenden Formeln anwenden:



Wir wenden die erste Formel an und erhalten:
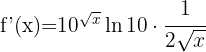
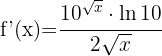
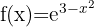
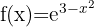
Wir wenden die zweite Formel an und erhalten::


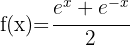
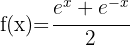
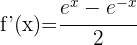
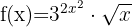
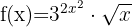
Wir wenden zuerst die Regel für Produkte an: 

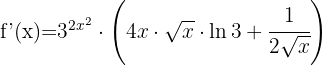
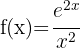
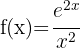
Wir wenden zuerst die Regel für Quotienten an: 
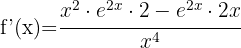
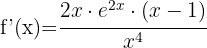

Berechne die Ableitungen der Logarithmusfunktionen
Berechne die Ableitungen der Logarithmusfunktionen
In dieser Aufgabe kommen folgende Formeln zum Einsatz:
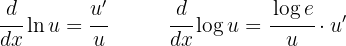
Außerdem können wir Logarithmusgesetze anwenden, um die Funktion in eine vereinfachte Form zu bringen und leichter ableiten zu können:
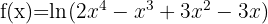
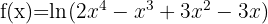
Wende die Formel für die Ableitung von Logarithmen an:
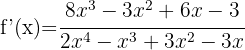


Wende die Logarithmusregel 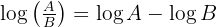 an und du erhältst:
an und du erhältst:

Leiten jeden der Terme mit der Formel für die Ableitung von Logarithmen ab:
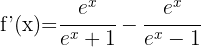
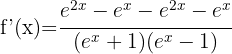
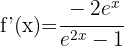


Wende die Logarithmusregeln 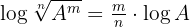 und
und 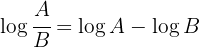 an und du erhältst:
an und du erhältst:

Wende die Formel für die Ableitung von Logarithmen an:


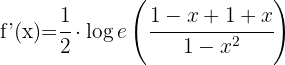
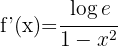
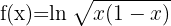
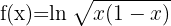
Wende die Logarithmusregeln 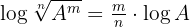 und
und 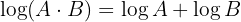 an und du erhältst:
an und du erhältst:
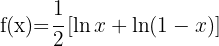
Wende die Formel für die Ableitung von Logarithmen an:
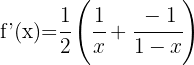
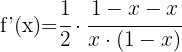
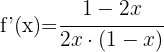
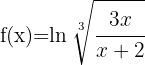
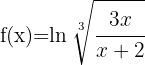
Wende die Logarithmusregeln 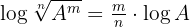 und
und 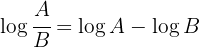 an und du erhältst:
an und du erhältst:

Wende die Formel für die Ableitung von Logarithmen an:

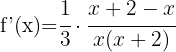

Mit KI zusammenfassen:













