
Was sind implizite Funktionen?
Implizite Funktionen sind solche, die sich auf 'x' und 'y' beziehen und bei denen keine der Variablen eindeutig ist. Um die Ableitung in impliziter Form zu ermitteln, ist es nicht notwendig, 'y' zu bestimmen und bei einigen impliziten Funktionen ist es sogar nicht möglich, 'y' zu bestimmen; es genügt, Glied für Glied nach den Regeln der Ableitung abzuleiten und dabei zu berücksichtigen, dass:
A x'=1
B Im Allgemeinen ist y'≠1
C Wir lassen also x' weg und behalten y' bei.
D Bei komplexeren Funktionen verwenden wir zur Erleichterung der Berechnung eine Regel:
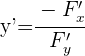
Aufgaben zu impliziten Funktionen
Leite die folgenden impliziten Funktionen ab

Leite  ab
ab
1 Wir leiten jeden Term einzeln ab.

2 Wir lösen nach y' auf




Leite  ab
ab
1 Wir leiten jeden Term einzeln ab: Denjenigen, der 'y' enthält, in Bezug auf 'y' und denjenigen, der 'x' enthält, in Bezug auf 'x'. Die Terme, die beide Variablen enthalten, werden zweimal abgeleitet, einmal in Bezug auf 'x' und einmal in Bezug auf 'y'.

2 Wir müssen y' ermitteln. Hierzu lassen wir die Terme, die y' enthalten, auf einer Seite und bringen die anderen Terme auf die andere Seite
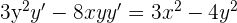
3 Wir klammern den gemeinsamen Faktor aus und lösen
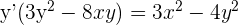
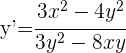
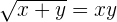
Leite 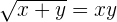 ab
ab
1 Wir leiten jeden Term einzeln ab. In diesem Fall müssen wir beide Terme ableiten, einmal in Bezug auf 'x' und einmal in Bezug auf 'y'.
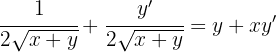
2 Wir müssen y' ermitteln. Hierzu lassen wir die Terme, die y' enthalten, auf einer Seite und bringen die anderen Terme auf die andere Seite
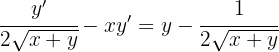
3 Wir führen die Berechnungen mit den Brüchen durch und klammern den gemeinsamen Faktor aus. Schließlich lösen wir nach y' auf'
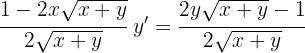

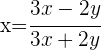
Leite 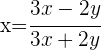 ab
ab
1 Wir leiten jeden Term einzeln ab, diejenigen, die 'x' und 'y' enthalten, werden zweimal abgeleitet. Für den zweiten Term der Gleichung müssen wir die Formel für die Ableitung eines Quotienten verwenden.

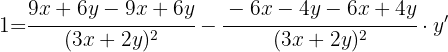

2 Wir müssen y' ermitteln. Hierzu lassen wir die Terme, die y' enthalten, auf einer Seite und bringen die anderen Terme auf die andere Seite. Wir führen die Berechnungen mit den Brüchen aus



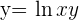
Leite 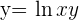 ab
ab
1 Wir leiten jeden Term einzeln ab. Denjenigen, der 'y' enthält, in Bezug auf 'y' und denjenigen, der 'x' enthält, in Bezug auf 'x'. Die Terme, die beide Variablen enthalten, werden zweimal abgeleitet, einmal in Bezug auf 'x' und einmal in Bezug auf 'y'.
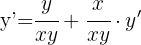
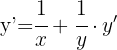
2 Wir müssen y' ermitteln. Hierzu lassen wir die Terme, die y' enthalten, auf einer Seite und bringen die anderen Terme auf die andere Seite
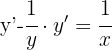
3 Wir klammern den gemeinsamen Faktor aus und lösen nach y' auf
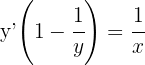
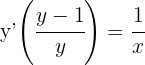

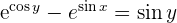
Leite 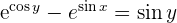 ab
ab
1 Da wir mehrere transzendente Funktionen haben, bringen wir alle Terme auf eine Seite der Gleichung. Wir wenden an: 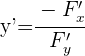
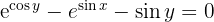
2 Wir berechnen  und
und 
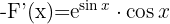
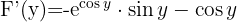
3 Wir setzen in 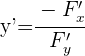 ein
ein

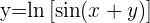
Leite 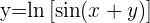 ab
ab
1 Da wir mehrere transzendente Funktionen haben, bringen wir alle Terme auf eine Seite der Gleichung. Wir wenden an: 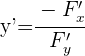

2 Wir berechnen  und
und 
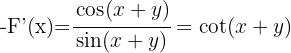
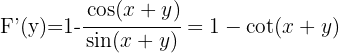
3 Wir setzen in 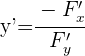 ein
ein


Leite  ab
ab
1 Wir berechnen  und
und 
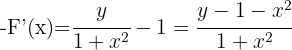
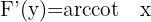
2 Wir setzen in 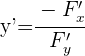 ein
ein


Leite  ab
ab
1 Wir multiplizieren beide Seiten mit  , um den Bruch zu eliminieren und bringen alle Terme auf eine Seite der Gleichung
, um den Bruch zu eliminieren und bringen alle Terme auf eine Seite der Gleichung
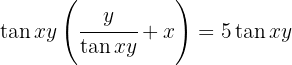

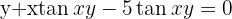
2 Wir berechnen  und
und 
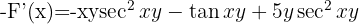

3 Wir setzen in 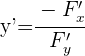 ein
ein
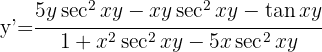

Leite  ab
ab
1 Da wir mehrere transzendente Funktionen haben, bringen wir alle Terme auf eine Seite der Gleichung. Wir wenden an: 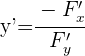
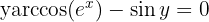
2 Wir berechnen  und
und 


3 Wir setzen in 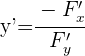 ein
ein

Mit KI zusammenfassen:












