Kapitel

Wie kann man feststellen, ob eine Funktion steigt oder fällt?
Eine Funktion  ist im Intervall
ist im Intervall 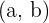 streng monoton steigend, wenn
streng monoton steigend, wenn 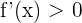 für alle Werte von
für alle Werte von  in
in 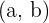 .
.
Eine Funktion  ist im Intervall
ist im Intervall 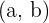 streng monoton fallend, wenn
streng monoton fallend, wenn 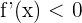 für alle Werte von
für alle Werte von  in
in 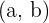 .
.
Intervalle des Monotonieverhaltens
Um die Intervalle 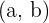 zu ermitteln, in denen die Funktion
zu ermitteln, in denen die Funktion  steigt oder fällt, führen wir folgende Schritte durch:
steigt oder fällt, führen wir folgende Schritte durch:
1 Wir leiten die Funktion ab.
2 Wir berechnen die Nullstellen der 1. Ableitung. Das heißt, wir finden die Werte  , für die
, für die 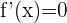 gilt.
gilt.
3 Wir bilden offene Intervalle mit den Nullstellen der 1. Ableitung und den Unstetigkeitsstellen (falls vorhanden).
4 Wir wählen einen Wert aus jedem Intervall und bestimmen das Vorzeichen der 1. Ableitung.
5 Wir wählen die Intervalle, in denen die Funktion steigt und fällt, entsprechend dem Vorzeichen, das wir im vorherigen Schritt ermittelt haben.
Aufgaben
Ermittle die Intervalle des Monotonieverhaltens von 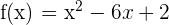
1 Wir leiten die Funktion ab.
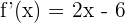
2 Wir berechnen die Nullstellen der 1. Ableitung. Hierfür setzen wir die Ableitung gleich 0 und lösen nach  auf
auf
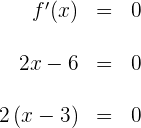
Wir setzen die Faktoren gleich 0 und erhalten die Nullstelle  .
.
3 Wir bilden offene Intervalle mit den Nullstellen der 1. Ableitung; in diesem Fall gibt es keine Unstetigkeitsstellen. Wir stützen uns dabei auf die Darstellung der Punkte auf der Zahlengeraden.
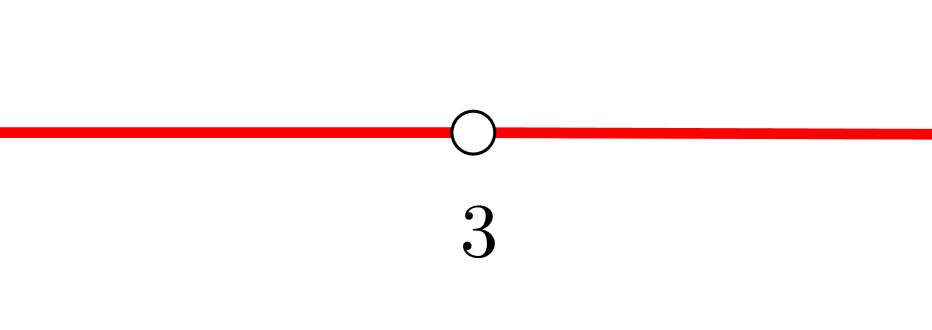
Wir erhalten die Intervalle  und
und 
4 Wir nehmen einen Wert in jedem Intervall (du kannst jeden Wert im Intervall nehmen) und finden das Vorzeichen, das er in der 1. Ableitung hat
Für das Intervall  nehmen wir
nehmen wir  . Wir setzen in die Ableitung ein und erhalten
. Wir setzen in die Ableitung ein und erhalten
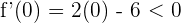
Für das Intervall  nehmen wir
nehmen wir 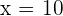 . Wir setzen in die Ableitung ein und erhalten
. Wir setzen in die Ableitung ein und erhalten
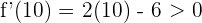
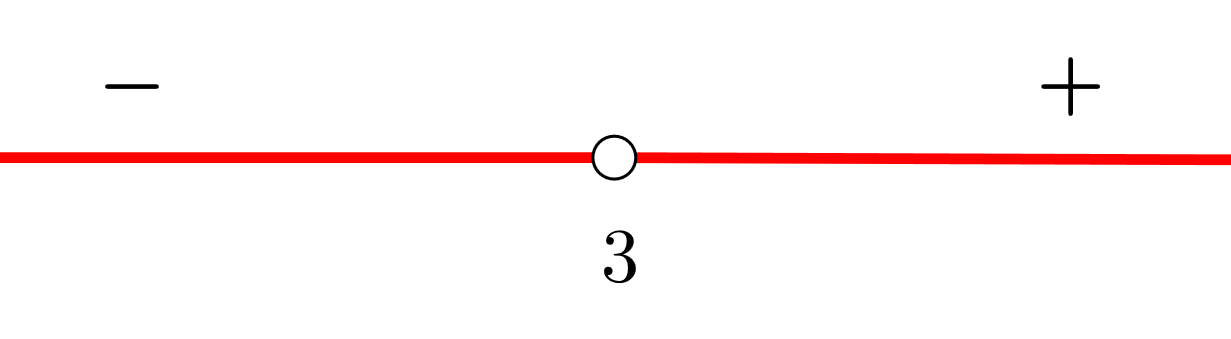
5 Wir schreiben die Intervalle des Monotonieverhaltens
Streng monoton steigend: 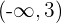
Streng monoton fallend: 
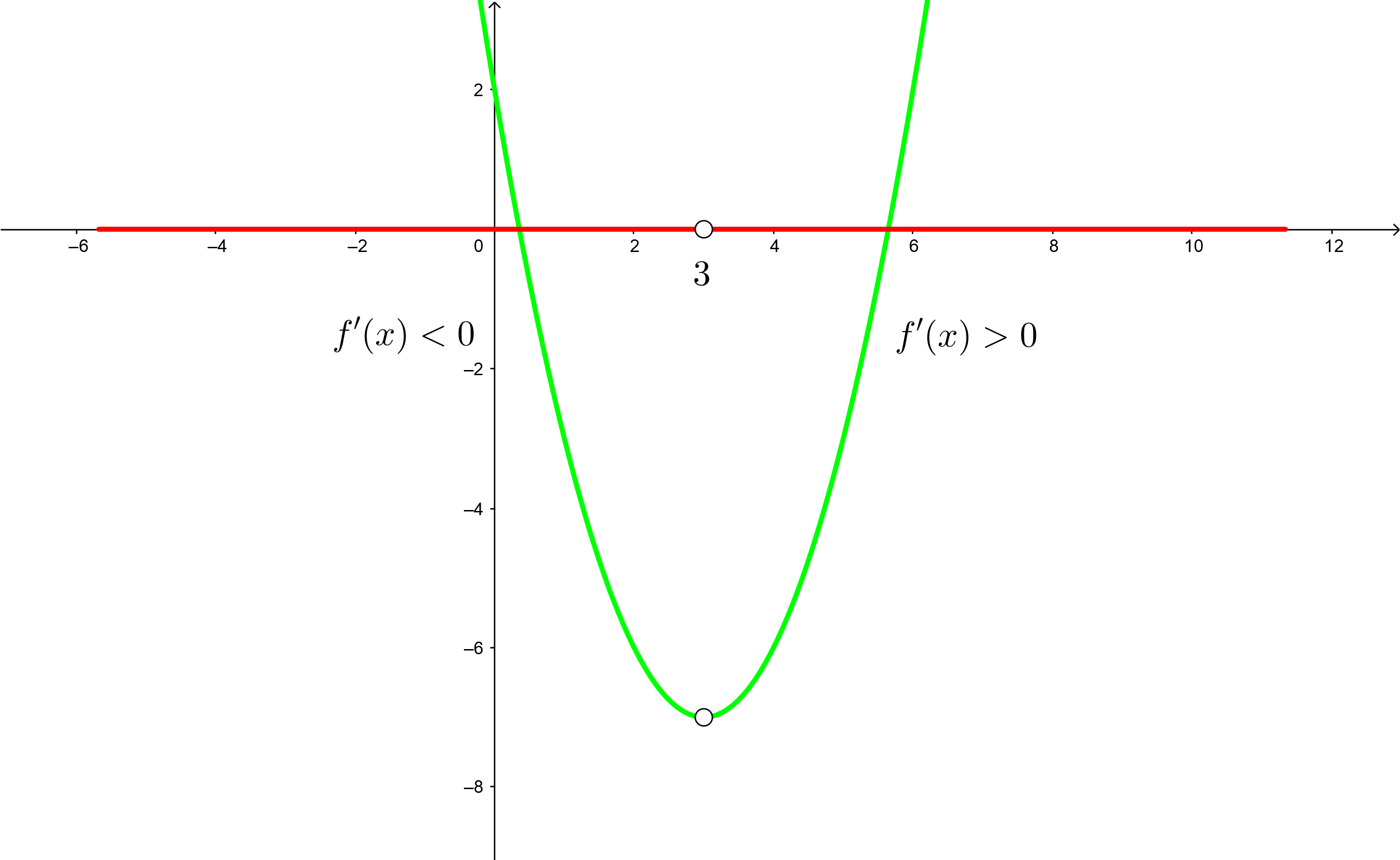
Ermittle die Intervalle des Monotonieverhaltens von 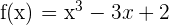
1 Wir leiten die Funktion ab
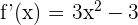
2 Wir berechnen die Nullstellen der 1. Ableitung. Hierzu setzen wir die Ableitung gleich 0 und lösen nach  auf
auf
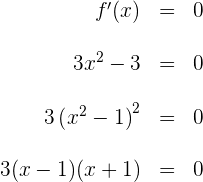
Wir setzen die Faktoren gleich 0 und erhalten die Nullstellen 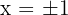 .
.
3 Wir bilden offene Intervalle mit den Nullstellen der 1. Ableitung. In diesem Fall gibt es keine Unstetigkeitsstellen. Wir stützen uns auf die Darstellung der Punkte auf der Zahlengeraden

Wir erhalten die Intervalle 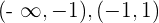 und
und 
4 Wir nehmen einen Wert in jedem Intervall (du kannst jeden Wert im Intervall nehmen) und finden das Vorzeichen, das er in der 1. Ableitung hat
Für das Intervall 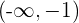 nehmen wir
nehmen wir  . Wir setzen in die Ableitung ein und erhalten
. Wir setzen in die Ableitung ein und erhalten
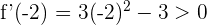
Für das Intervall  nehmen wir
nehmen wir  . Wir setzen in die Ableitung ein und erhalten
. Wir setzen in die Ableitung ein und erhalten
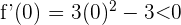
Für das Intervall  nehmen wir
nehmen wir  . Wir setzen in die Ableitung ein und erhalten
. Wir setzen in die Ableitung ein und erhalten
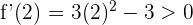

5 Wir schreiben die Intervalle des Monotonieverhaltens
Streng monoton steigend: 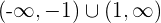
Streng monoton fallend: 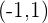
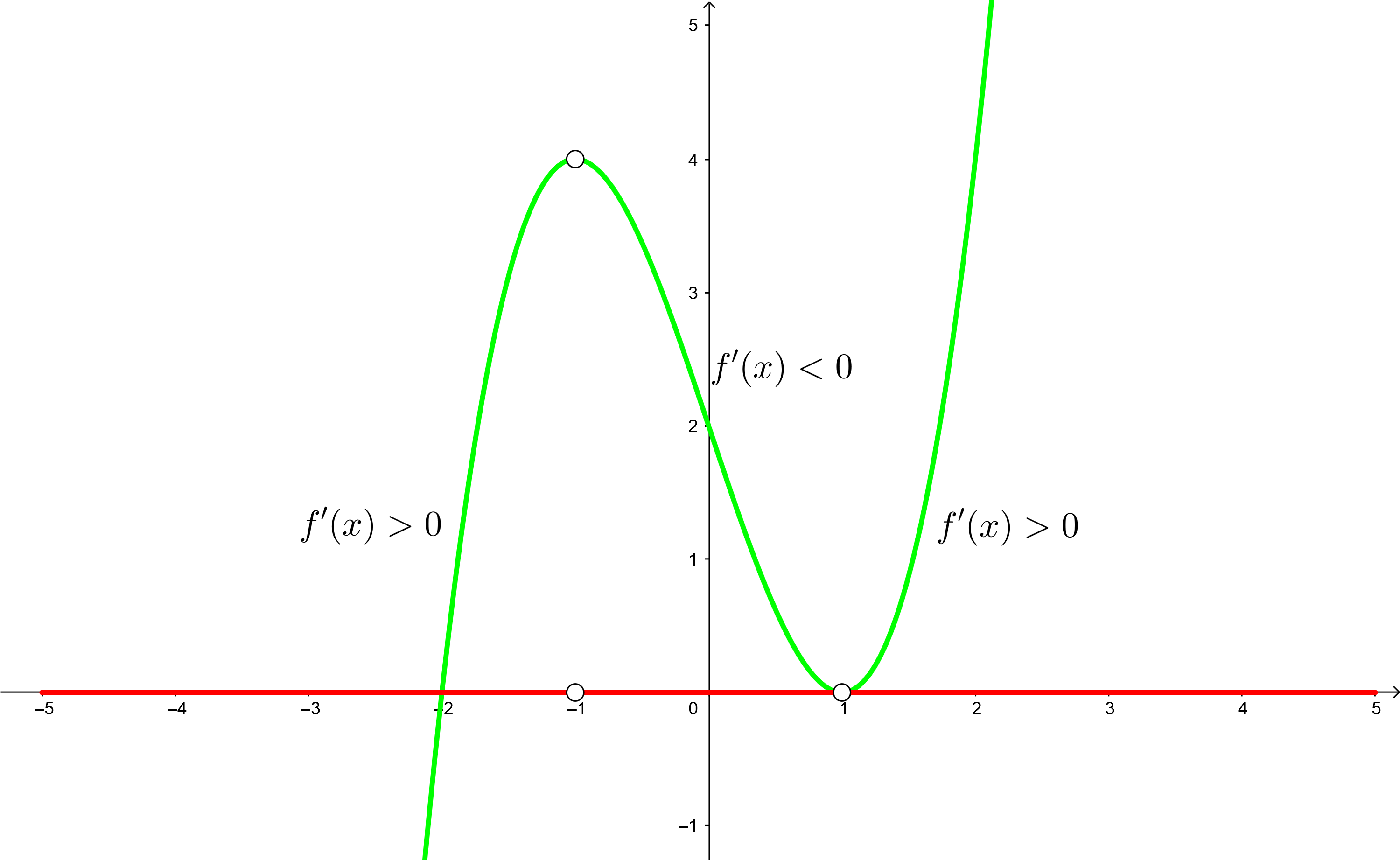
Bestimme die Intervalle des Monotonieverhaltens von 
1 Wir leiten die Funktion ab
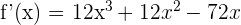
2 Wir berechnen die Nullstellen der 1. Ableitung. Hierzu setzen wir die Ableitung gleich 0 und lösen nach  auf
auf
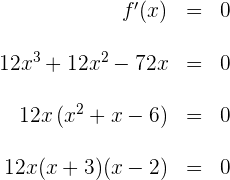
Wir setzen die Faktoren gleich 0 und erhalten die Nullstellen 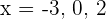 .
.
3 Wir bilden offene Intervalle mit den Nullstellen der 1. Ableitung. In diesem Fall gibt es keine Unstetigkeitsstellen. Wir stützen uns auf die Darstellung der Punkte auf der Zahlengeraden
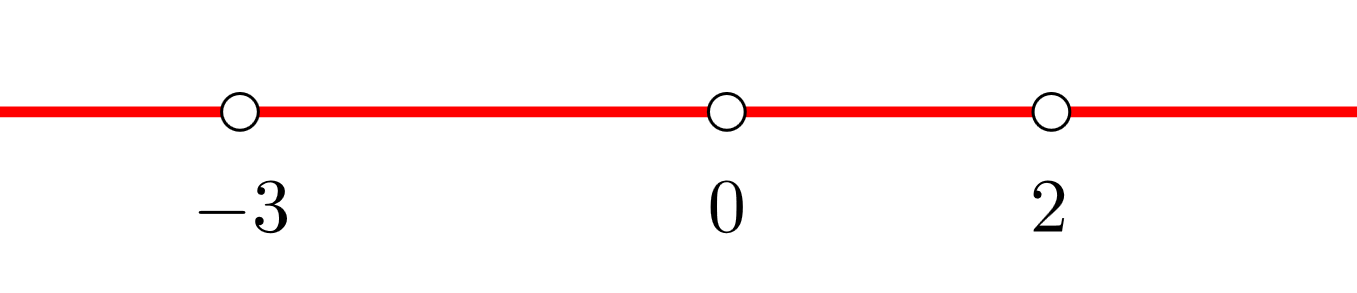
5 Wir schreiben die Intervalle des Monotonieverhaltens
Streng monoton fallend: 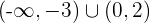
Streng monoton steigend: 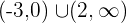
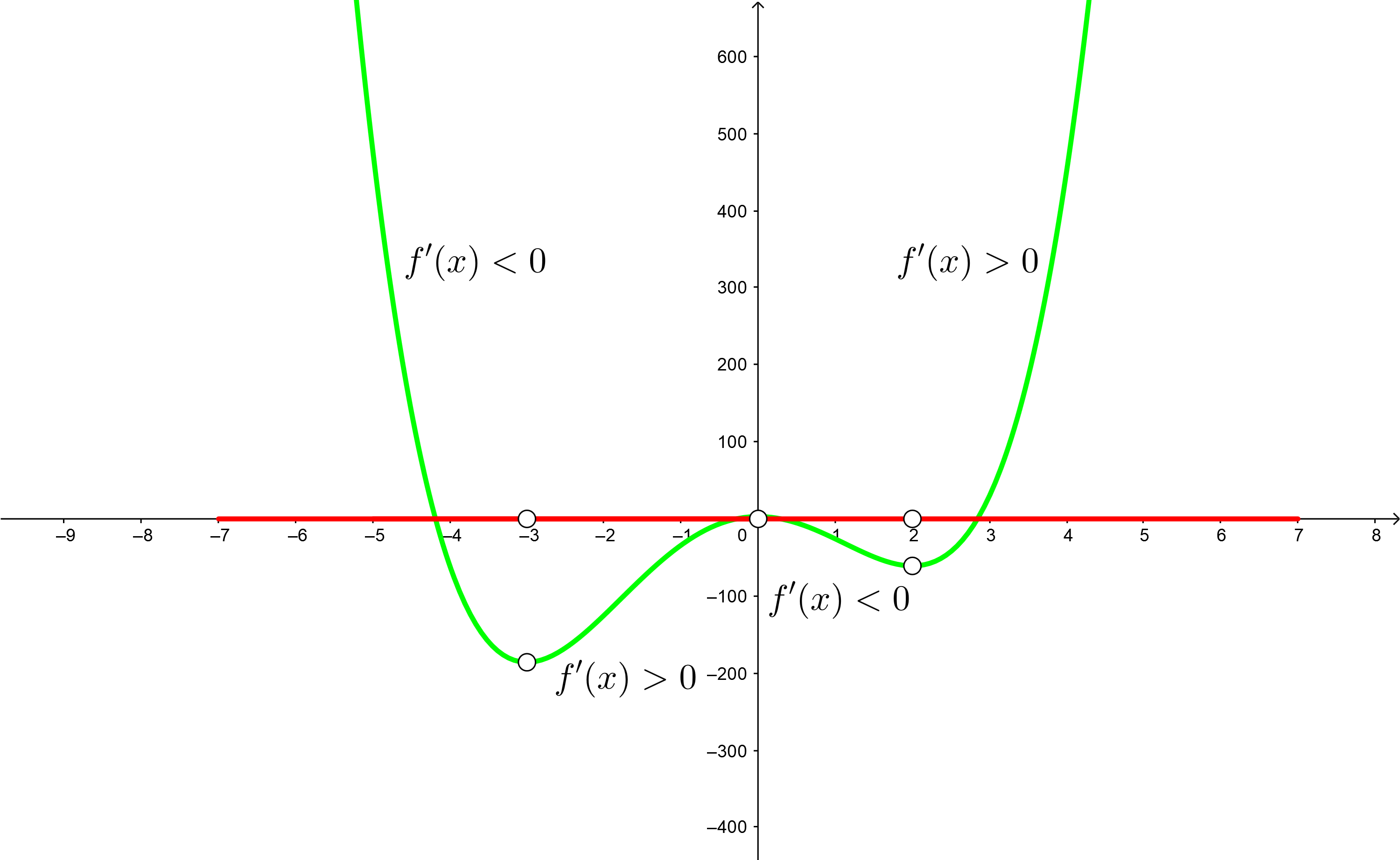
Bestimme die Intervalle, in denen die Funktion  steigt und fällt
steigt und fällt
1 Wir leiten die Funktion ab

2 Wir berechnen die Nullstellen der 1. Ableitung (sofern es welche gibt). Hierzu setzen wir die Ableitung gleich 0 und lösen nach  auf
auf
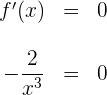
Es gibt keine Werte für  in den reellen Zahlen, die die obige Gleichung erfüllen, also hat die 1. Ableitung keine Nullstellen. Wir stellen fest, dass die Funktion und ihre Ableitung eine Unstetigkeitsstelle bei
in den reellen Zahlen, die die obige Gleichung erfüllen, also hat die 1. Ableitung keine Nullstellen. Wir stellen fest, dass die Funktion und ihre Ableitung eine Unstetigkeitsstelle bei  haben.
haben.
3 Wir bilden offene Intervalle mit der Unstetigkeitsstelle; in diesem Fall hat die Ableitung keine Nullstellen. Wir stützen uns auf die Darstellung der Punkte auf der Zahlengeraden
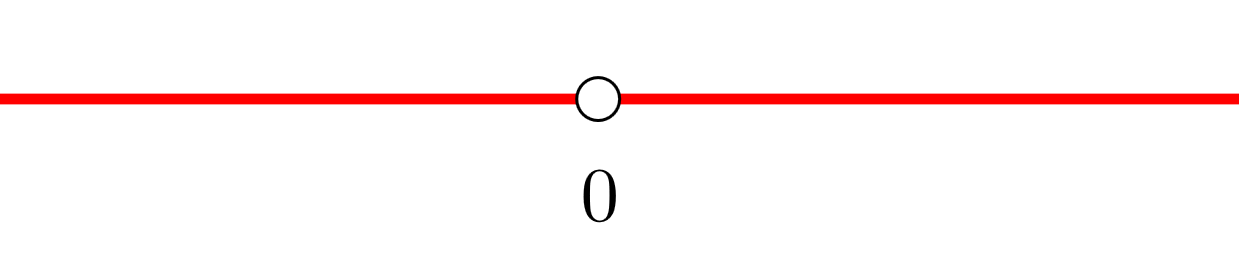
Wir erhalten die Intervalle 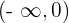 und
und 
4 Wir nehmen einen Wert in jedem Intervall (du kannst jeden Wert im Intervall nehmen) und finden das Vorzeichen, das er in der 1. Ableitung hat
Für das Intervall  nehmen wir
nehmen wir  . Wir setzen in die Ableitung ein und erhalten
. Wir setzen in die Ableitung ein und erhalten
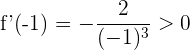
Für das Intervall 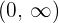 nehmen wir
nehmen wir  . Wir setzen in die Ableitung ein und erhalten
. Wir setzen in die Ableitung ein und erhalten
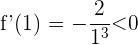

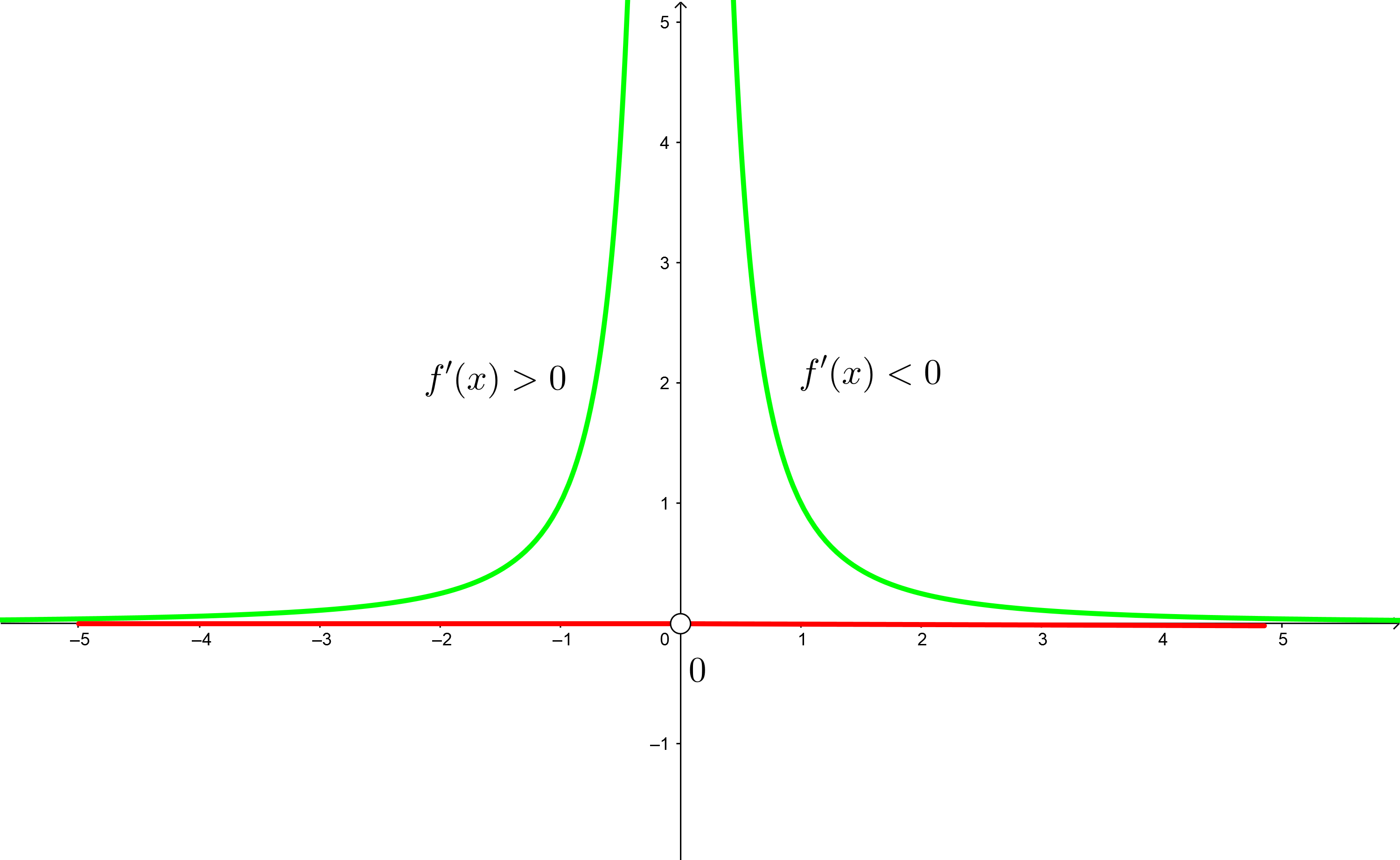
5 Wir schreiben die Intervalle des Monotonieverhaltens
Streng monoton steigend: 
Streng monoton fallend: 
Bestimme die Intervalle, in denen die Funktion  steigt und fällt
steigt und fällt
1 Wir leiten die Funktion ab
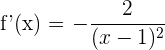
2 Wir berechnen die Nullstellen der 1. Ableitung (sofern es welche gibt). Hierfür setzen wir die Ableitung gleich 0 und lösen nach  auf
auf

Es gibt keine Werte für  in den natürlichen Zahlen, die die vorherige Gleichung erfüllen. Die Ableitung besitzt also keine Nullstellen. Allerdings haben die Funktion und ihre Ableitung eine Unstetigkeitsstelle bei
in den natürlichen Zahlen, die die vorherige Gleichung erfüllen. Die Ableitung besitzt also keine Nullstellen. Allerdings haben die Funktion und ihre Ableitung eine Unstetigkeitsstelle bei  .
.
3 Wir bilden offene Intervalle mit der Unstetigkeitsstelle. In diesem Fall besitzt die Ableitung keine Nullstellen. Wir stützen uns auf die Darstellung der Punkte auf der Zahlengeraden
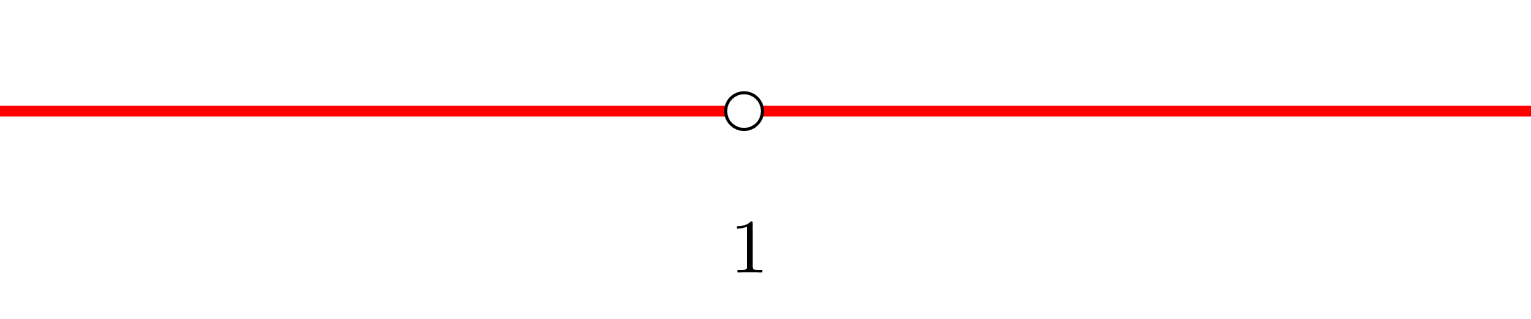
Wir erhalten die Intervalle 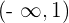 und
und 
4 Wir nehmen einen Wert in jedem Intervall (du kannst jeden Wert im Intervall nehmen) und finden das Vorzeichen, das er in der 1. Ableitung hat
Für das Intervall  nehmen wir
nehmen wir  . Wir setzen in die Ableitung ein und erhalten
. Wir setzen in die Ableitung ein und erhalten
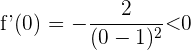
Für das Intervall  nehmen wir
nehmen wir  . Wir setzen in die Ableitung ein und erhalten
. Wir setzen in die Ableitung ein und erhalten
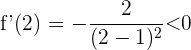
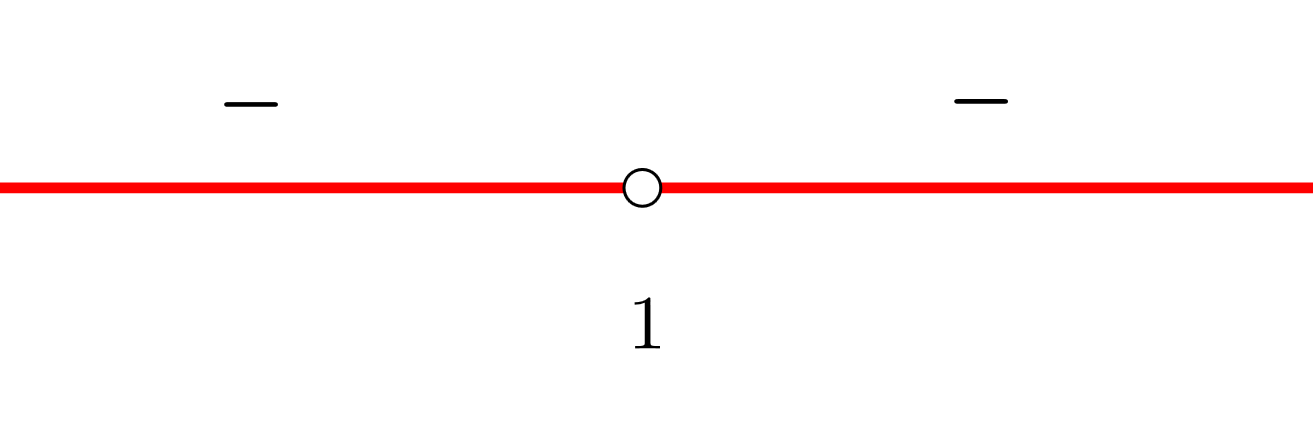
5 Da das Ergebnis bei der Auswertung in der Ableitung immer negativ war, hat man nur Intervalle, in denen die Funktion fällt
Streng monoton fallend: 
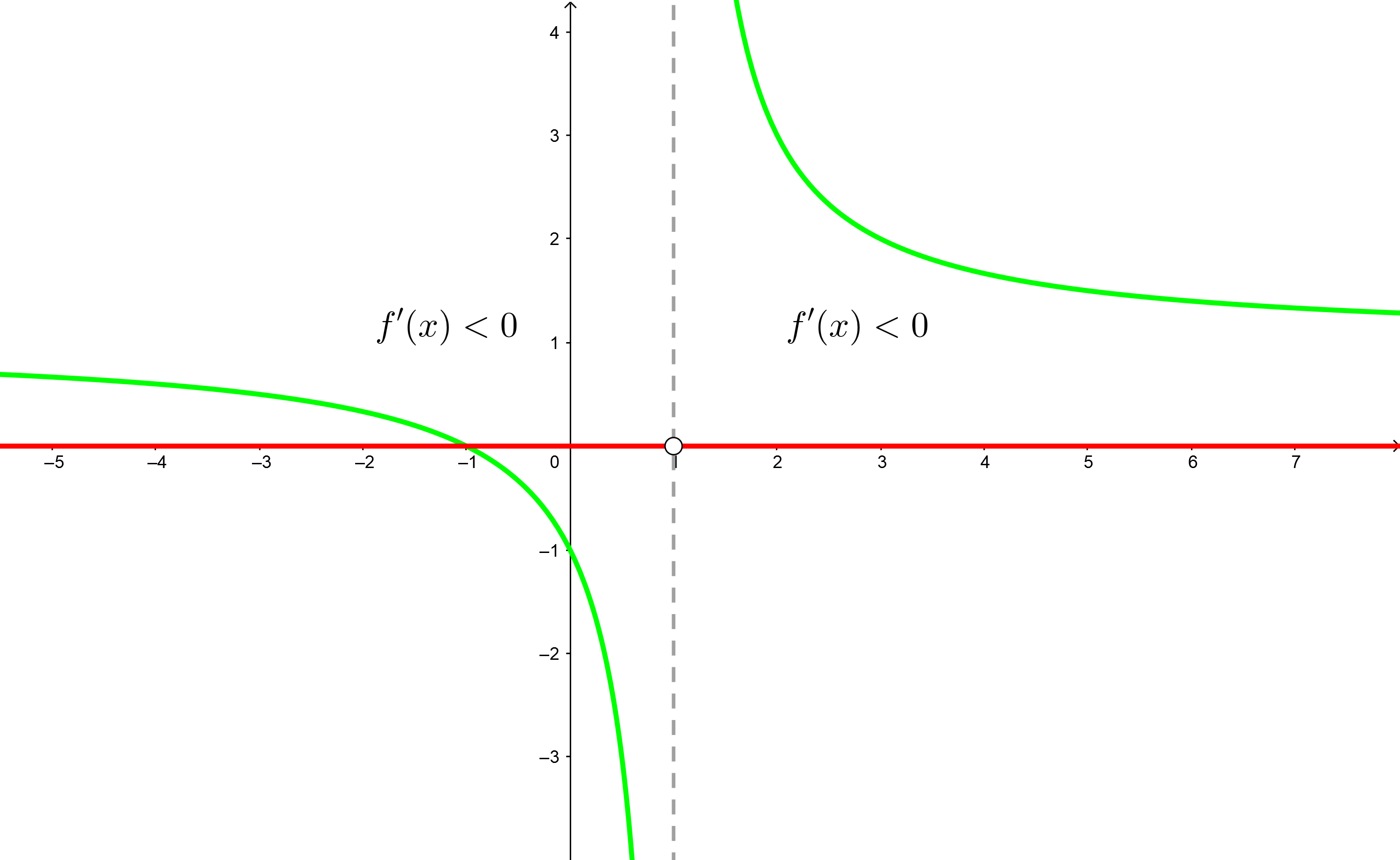
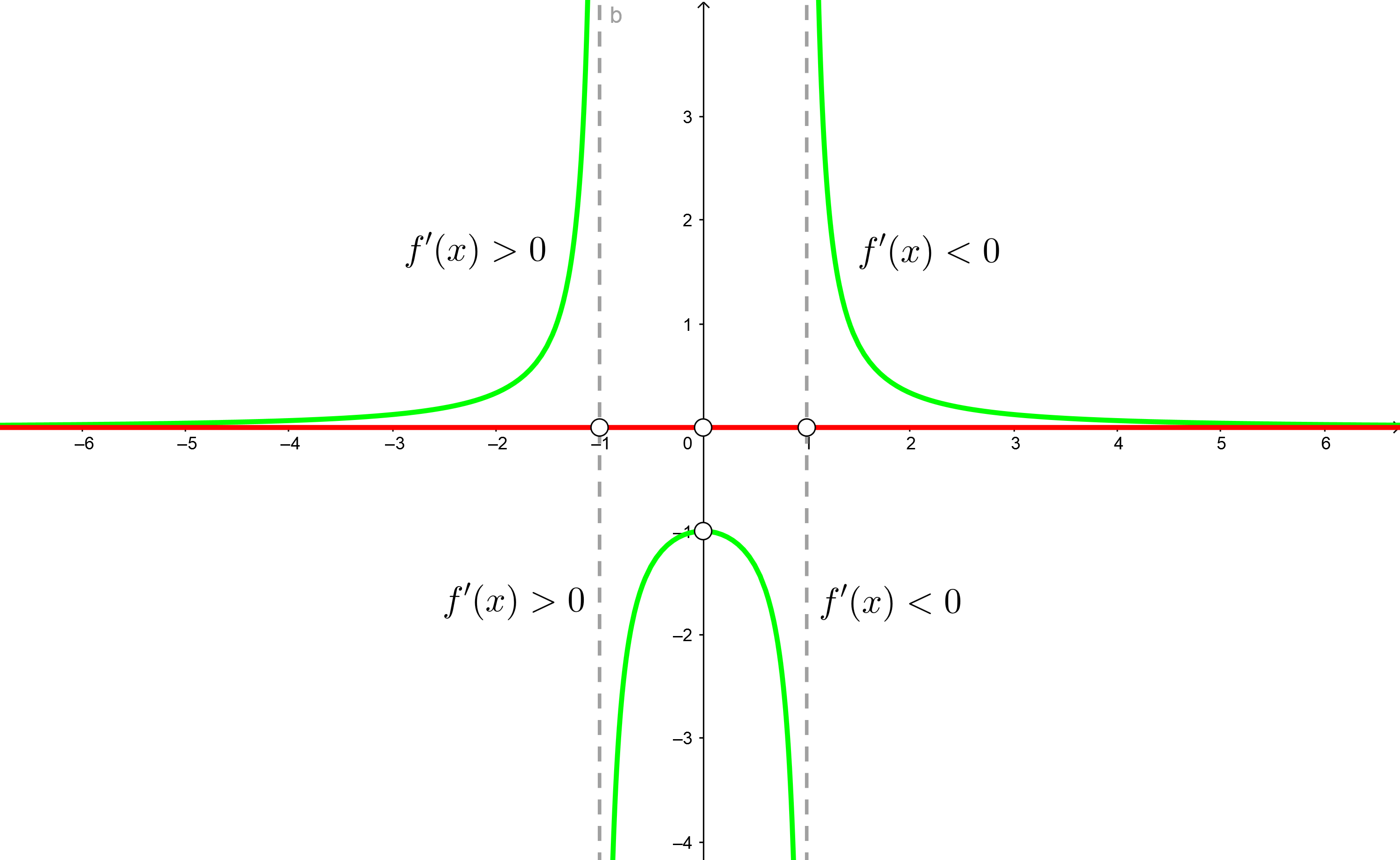
Bestimme die Intervalle, in denen die Funktion  steigt und fällt
steigt und fällt
1 Wir leiten die Funktion ab
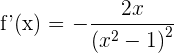
2 Wir berechnen die Nullstellen der 1. Ableitung (sofern es welche gibt). Hierfür setzen wir die Ableitung gleich 0 und lösen nach  auf
auf

 ist der einzige Wert, der die obige Gleichung erfüllt. Wir stellen fest, dass die Funktion und ihre Ableitung Unstetigkeitsstellen bei
ist der einzige Wert, der die obige Gleichung erfüllt. Wir stellen fest, dass die Funktion und ihre Ableitung Unstetigkeitsstellen bei 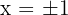 besitzen.
besitzen.
3 Wir bilden offene Intervalle mit den Unstetigkeitsstellen und der Nullstelle der Ableitung. Wir stützen uns auf die Darstellung der Punkte auf der Zahlengeraden
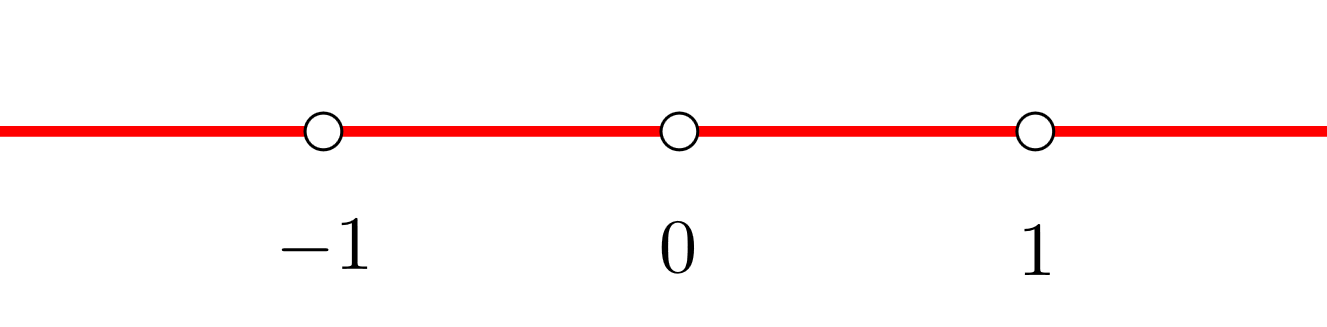
Wir erhalten die Intervalle  und
und 
4 Wir nehmen einen Wert in jedem Intervall (du kannst jeden Wert im Intervall nehmen) und finden das Vorzeichen, das er in der 1. Ableitung hat
Für das Intervall 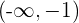 nehmen wir
nehmen wir  . Wir setzen in die Ableitung ein und erhalten
. Wir setzen in die Ableitung ein und erhalten

Für das Intervall  nehmen wir
nehmen wir 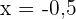 . Wir setzen in die Ableitung ein und erhalten
. Wir setzen in die Ableitung ein und erhalten
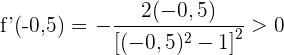
Für das Intervall  nehmen wir
nehmen wir 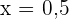 . Wir setzen in die Ableitung ein und erhalten
. Wir setzen in die Ableitung ein und erhalten
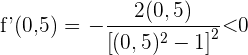
Für das Intervall  nehmen wir
nehmen wir  . Wir setzen in die Ableitung ein und erhalten
. Wir setzen in die Ableitung ein und erhalten
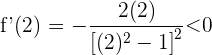
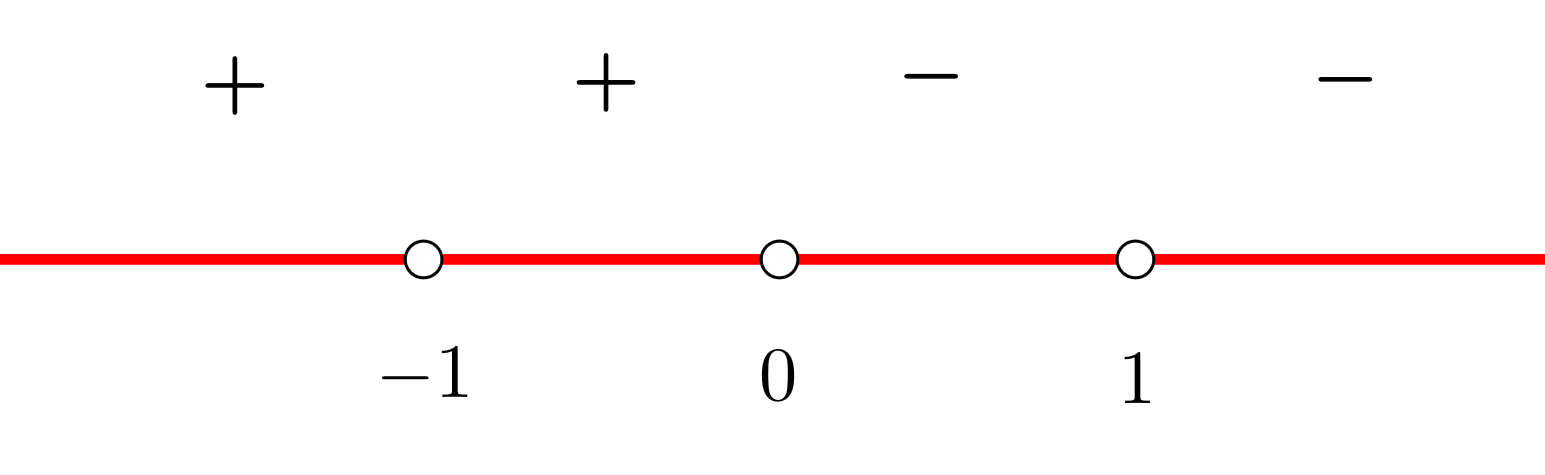
5 Wir schreiben die Intervalle des Monotonieverhaltens
Streng monoton steigend: 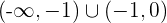
Streng monoton fallend: 
Mit KI zusammenfassen:












