Kapitel
Die Ableitung einer Funktion ist eines der wichtigsten Konzepte der Berechnung. Die Ableitung findet auch in vielen anderen Bereichen Anwendung, z. B. im Finanzwesen, in der Chemie, Physik und Biologie. Im Folgenden findest du eine Übersicht über die gängigsten Funktionen und ihre jeweiligen Ableitungen.

Ableitung der Identitätsfunktion
Die einfachste Funktion, die wir finden können, ist die Identitätsfunktion.
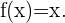
In diesem Fall ist die Ableitung von x, notiert mit 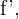 , gleich 1. Das heißt, die Ableitung der Identitätsfunktion ist gleich der Einheit.
, gleich 1. Das heißt, die Ableitung der Identitätsfunktion ist gleich der Einheit.

Ableitung einer Potenz zur Basis x
Um die Ableitung einer Potenz von 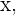 zu ermitteln, müssen wir nur den Exponenten nehmen, ihn vor das x schreiben (also mit ihm multiplizieren) und den Exponenten gleichzeitig um 1 reduzieren. Das heißt:
zu ermitteln, müssen wir nur den Exponenten nehmen, ihn vor das x schreiben (also mit ihm multiplizieren) und den Exponenten gleichzeitig um 1 reduzieren. Das heißt:
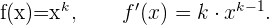
Ableitung einer Wurzel mit dem Radikanden x
Die Ableitung eines Radikanden der Variablen  lässt sich durch die Ableitung einer Potenz ermitteln.
lässt sich durch die Ableitung einer Potenz ermitteln.
Wenn wir 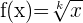 ableiten möchten, können wir den Ausdruck dieser Funktion ändern, um eine bereits bekannte Formel zu verwenden und die Ableitung zu berechnen. Wir denken daran, dass ein äquivalenter Ausdruck für
ableiten möchten, können wir den Ausdruck dieser Funktion ändern, um eine bereits bekannte Formel zu verwenden und die Ableitung zu berechnen. Wir denken daran, dass ein äquivalenter Ausdruck für  wie folgt lautet
wie folgt lautet
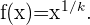
Wenn wir also die Ableitung einer Potenz auf 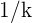 anwenden, wissen wir, dass wir mit
anwenden, wissen wir, dass wir mit 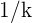 multiplizieren müssen. Der neue Exponent lautet
multiplizieren müssen. Der neue Exponent lautet
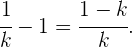
Und somit für 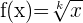
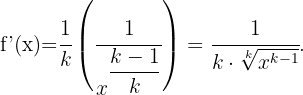
Ein Sonderfall ist die Ableitung einer Quadratwurzel, die jedoch eine der häufigsten ist. Diese lautet

Ableitungen von Exponential- und Logarithmusfunktionen
Ableitungen von Exponential- und Logarithmusfunktionen kommen in der Physik bei der Untersuchung von Mechanik, elektrischen Feldern und Optik vor. Man findet sie auch bei der Untersuchung homogener Gleichungen im Bereich der Differentialgleichungen.
Ableitung der Exponentialfunktion mit dem Exponenten x
Es ist wichtig zu beachten, dass es bei der Ableitung einer Exponentialfunktion immer um die Funktion multipliziert mit dem natürlichen Logarithmus der Basis geht. Das heißt:
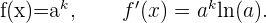
Eine der wichtigsten Ableitungen ist die Ableitung der Exponentialfunktion mit der Basis  . Der Logik des vorigen Absatzes folgend, erhalten wir
. Der Logik des vorigen Absatzes folgend, erhalten wir

und somit 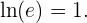
Ableitung des Logarithmus von x
Die Logarithmusableitung wurde von Newton und Leibniz, den Begründern der Infinitesimalrechnung, entdeckt. Diese Ableitung findet sich auch in der Physik und bei der Untersuchung von Funktionen mit komplexen Variablen. Eine Logarithmusfunktion  hat als Ableitung folgende Funktion
hat als Ableitung folgende Funktion

Ein Sonderfall ist die Logarithmusableitung zur Basis 
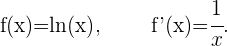
Trigonometrische Ableitungen
Trigonometrische Funktionen sind Teil der Untersuchung von Bewegung und der Wechselwirkung von Kräften. Ein wichtiger Teil des Verständnisses von Bewegung ist das Verständnis der Änderungsrate der Position in Bezug auf die Zeit, d. h. der Geschwindigkeit – genauer gesagt der Ableitung. Die Bewegungen verlaufen nicht immer nur in eine Richtung. Im Allgemeinen müssen wir die Bewegungsvektoren in mehrere Koordinaten zerlegen. Hier kommen die trigonometrischen Funktionen und ihre Ableitungen ins Spiel. In den folgenden Abschnitten findest du die trigonometrischen Funktionen mit ihren jeweiligen Ableitungen.
Ableitung des Sinus von x

Ableitung des Kosinus von x

Ableitung des Tangens von x
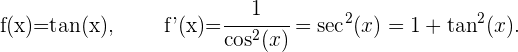
Ableitung des Kotangens von x
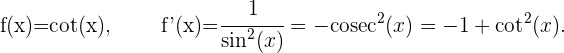
Ableitung des Sekans von x
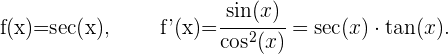
Ableitung des Kosekans von x
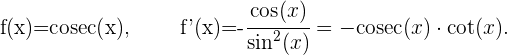
Ableitungen von trigonometrischen Umkehrfunktionen
Als Ergänzung zum Studium der trigonometrischen Funktionen müssen wir immer uns auch immer mit den trigonometrischen Umkehrfunktionen befassen.
Hierzu ein Beispiel: Beim Zerlegen eines Vektors  in der Ebene in seine Komponenten
in der Ebene in seine Komponenten  und
und  , gilt, dass
, gilt, dass 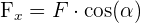 und
und 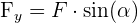 , wobei
, wobei  der Winkel ist, den der Vektor
der Winkel ist, den der Vektor  mit der
mit der  -Achse bildet. Dieser Winkel
-Achse bildet. Dieser Winkel  kann ermittelt werden, indem wir trigonometrische Umkehrfunktionen anwenden:
kann ermittelt werden, indem wir trigonometrische Umkehrfunktionen anwenden: 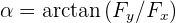 . Wenn sich dieser Winkel in Bezug auf eine andere Variable im System zu ändern beginnt, ist es wichtig, das Verhältnis zu kennen, mit dem diese Änderungen auftreten. Es ist also wichtig, die Ableitung der trigonometrischen Umkehrfunktion
. Wenn sich dieser Winkel in Bezug auf eine andere Variable im System zu ändern beginnt, ist es wichtig, das Verhältnis zu kennen, mit dem diese Änderungen auftreten. Es ist also wichtig, die Ableitung der trigonometrischen Umkehrfunktion 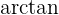 zu kennen.
zu kennen.
Nachstehend folgt eine Liste der trigonometrischen Funktionen mit ihren jeweiligen Ableitungen.
Ableitung des Arkussinus von x
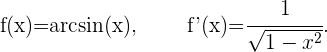
Ableitung des Arkuskosinus von x
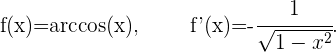
Ableitung des Arkustanges von x
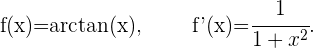
Ableitung des Arkuskotangens von x
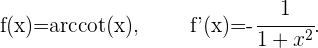
Ableitung des Arkussekans von x
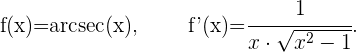
Ableitung des Arkuskosekans von x
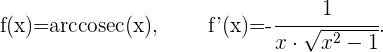
Mit KI zusammenfassen:












