Kapitel
Satz von Bolzano und Nullstellen einer Funktion
Bernhard Placidus Johann Bolzano (1781-1848) war ein tschechischer Mathematiker, der sich mit dem Konzept der Stetigkeit beschäftigte. Eines seiner Ergebnisse ist der Satz, der seinen Namen trägt.
Satz von Bolzano. Wenn 
eine stetige Funktion in einem geschlossenen Intervall 
ist, die an den Extrema Werte mit umgekehrtem Vorzeichen annimmt, so existiert mindestens ein Wert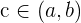 
, sodass 
.
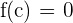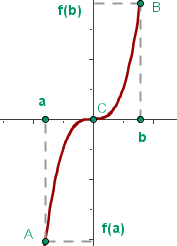
In diesem Satz ist es von äußerster Wichtigkeit, dass die Funktion stetig ist, was uns erlaubt, ihren Graphen als eine aus einem einzigen Stück bestehende Linie darzustellen. Wenn die horizontale Gerade 
die 
-Achse darstellt und die Enden der Linie auf gegenüberliegenden Seiten der -Achse liegen, dann muss die Linie über dieser Koordinatenachse verlaufen. Das heißt, sie schneidet die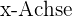 
und ist somit eine Nullstelle der Funktion.
Es sei darauf hingewiesen, dass der Satz von Bolzano auf die Existenz eines Wertes 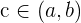hinweist, sodass 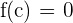ist, aber nicht beschreibt, wie man diesen Wert ermitteln kann.
Der Satz von Bolzano zeigt nicht nur das Vorhandensein einer Nullstelle an, sondern kann auch dazu verwendet werden, die Existenz eines Wertes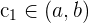 
zu garantieren, sodass 
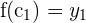für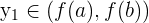 
. Es genügt, die oben erwähnte Linie zu betrachten und die horizontale Gerade 
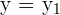zu berücksichtigen.
Eine der Anwendungen des Satzes von Bolzano ist die folgende: Angenommen, man reist mit dem Auto von einer Stadt 
zu einer Stadt 
, fährt um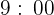 
Uhr los und kommt am selben Tag an. Wenn man am nächsten Tag zur gleichen Zeit wie auf der Hinfahrt in die Stadt fährt, dann gibt es einen Punkt während der Fahrt, an dem sich das Auto an beiden Tagen zur selben Zeit befindet.
Um dieses Problem zu verstehen, ohne den Satz von Bolzano anwenden zu müssen, betrachten wir die zurückgelegte Strecke und platzieren zwei Autos – eines in jeder Stadt – die ihre Fahrt zur gleichen Zeit beginnen. So kann man sich leicht vorstellen, dass sich die beiden Autos irgendwo auf dem Weg begegnen werden.
Unter Verwendung des Satzes von Bolzano betrachten wir 
als die Funktion der auf der Hinfahrt zurückgelegten Strecke in der Zeit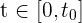 
. Das heißt, 
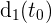ist gleich der Entfernung, die von Stadt nach Stadt zurückgelegt wird. Analog dazu ist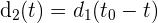 
die Funktion der auf dem Rückweg zurückgelegten Strecke in der Zeit .
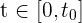Es kann die Funktion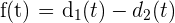 
erstellt werden, die stetig ist, da die Funktion der Distanz stetig ist. Somit gilt:
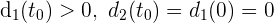
Wenn wir also die Funktion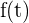 
an den Extremwerten des Intervalls 
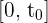auswerten, erhalten wir
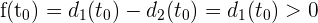
Da die Vorzeichen an den Grenzwerten des Intervalls unterschiedlich sind, können wir den Satz von Bolzano anwenden. Es existiert also ein Wert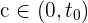 
, sodass 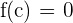. Daraus ergibt sich
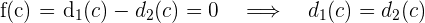
Das Auto befindet sich also an beiden Tagen zur gleichen Zeit am gleichen Punkt.
Wie du siehst, betrachten wir in diesem Beispiel nicht die explizite Form der Abstandsfunktion. Im Folgenden findest du eine Reihe von Beispielen, bei denen die zu verwendenden Funktionen in expliziter Form angegeben sind.
Beispiele für Fälle, in denen der Satz von Bolzano Anwendung findet
1 Zeige, dass die Funktion 
mindestens eine reelle Lösung im Intervall 
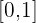hat.
Wir betrachten die Funktion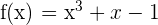 
, die in 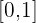stetig ist, da sie eine Polynomfunktion ist.
Wir untersuchen das Vorzeichen an den Extremwerten des Intervalls:
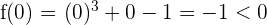
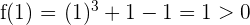
Da die Vorzeichen unterschiedliche sind, können wir den Satz von Bolzano anwenden. Es existiert also ein Wert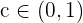 
, sodass 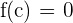. Dies zeigt, dass es eine Lösung in diesem Intervall gibt.
2Zeige, dass die Gleichung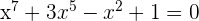 
mindestens eine reelle Lösung im Intervall 
hat.
Wir betrachten die Funktion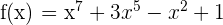 
, die in stetig ist, da sie eine Polynomfunktion ist.
Wir untersuchen das Vorzeichen an den Extremwerten des Intervalls:
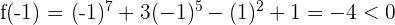
Da die Vorzeichen unterschiedlich sind, können wir den Satz von Bolzano anwenden. Es existiert also ein Wert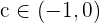 
, sodass 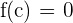. Dies zeigt, dass es eine Lösung in diesem Intervall gibt.
3Zeige, dass die Gleichung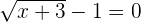 
mindestens eine reelle Lösung im Intervall 
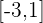hat.
Wir betrachten die Funktion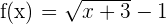 
, die in 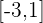stetig ist, da es sich um eine Differenz von stetigen Funktionen handelt. Die Definitionsmenge ist 
.
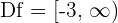Wir untersuchen das Vorzeichen an den Extremwerten des Intervalls:
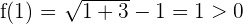
Da die Vorzeichen unterschiedlich sind, können wir den Satz von Bolzano anwenden. Es existiert also ein Wert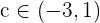 
, sodass 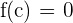. Dies zeigt, dass es eine Lösung in diesem Intervall gibt.
4Zeige, dass die Gleichung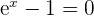 
mindestens eine reelle Lösung im Intervall 
hat.
Wir betrachten die Funktion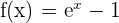 
, die in stetig ist, da sie innerhalb von 
eine Differenz von stetigen Funktionen ist.
Wir untersuchen das Vorzeichen an den Extremwerten des Intervalls:
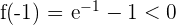
Da die Vorzeichen unterschiedlich sind, können wir den Satz von Bolzano anwenden. Es existiert also ein Wert 
, sodass 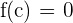. Dies zeigt, dass es eine Lösung in diesem Intervall gibt.
5 Zeige, dass die Gleichung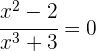 
mindestens eine reelle Lösung im Intervall 
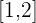hat.
Wir betrachten die Funktion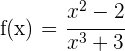 
, die in 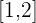stetig ist, da es sich um einen Quotienten aus Polynomen handelt und ihre Definitionsmenge 
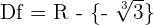ist.
Wir untersuchen das Vorzeichen an den Extremwerten des Intervalls:
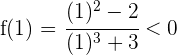
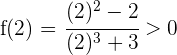
Da die Vorzeichen unterschiedlich sind, können wir den Satz von Bolzano anwenden. Es existiert also ein Wert 
, sodass 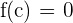. Dies zeigt, dass es eine Lösung in diesem Intervall gibt.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
