Gegeben sei die Funktion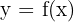 
und betrachten wir zwei nahe beieinander liegende Punkte auf der x-Achse 
und 
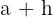, wobei 
eine reelle Zahl ist, die der Zunahme von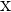 
(
) entspricht.
Die Differenz zwischen den entsprechenden Ordinaten und den Punkten und 
auf der x-Achse wird Änderungsrate der Funktion auf dem Intervall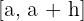 
genannt und mit 
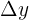angegeben.
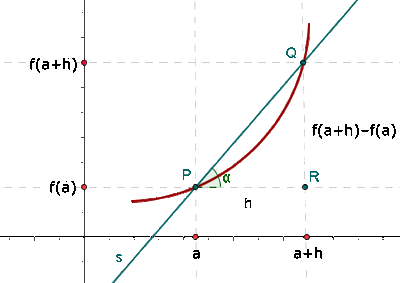
Die durchschnittliche Änderungsrate
Der Quotient aus der Änderungsrate und der Breite des betrachteten Intervalls auf der x-Achse wird durchschnittliche Änderungsrate auf dem Intervall 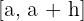genannt und mit 
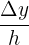oder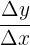 
angegeben. Das heißt,
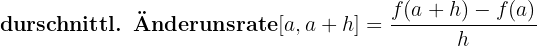
Geometrische Interpretation
Der vorherige Ausdruck stimmt mit der Steigung der Sekante an die Funktion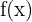 
überein, die durch die Punkte und auf der x-Achse verläuft.
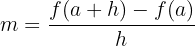
Da im Dreieck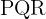 
aus der obigen Abbildung Folgendes gilt:
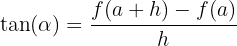
Beispiele
1 Berechne die durchschnittliche Änderungsrate der Funktion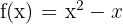 
auf dem Intervall 
.
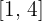2 Der Index der Madrider Börse stieg in einem bestimmten Jahr von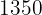 
auf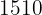 
. Berechne die monatliche durchschnittliche Änderungsrate.
Mit KI zusammenfassen:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
