Wenn f(x) eine ableitbare Funktion ist, ist das Differential einer Funktion, die dem Zuwachs h der unabhängigen Variablen entspricht, das Produkt f'(x) · h.
Das Differential einer Funktion wird mit dy ausgedrückt.
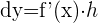
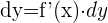
Geometrische Interpretation
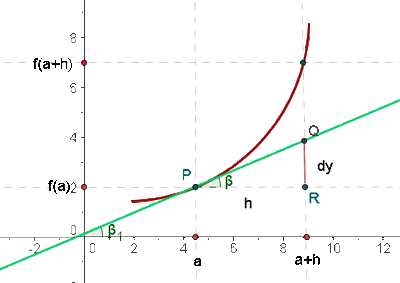
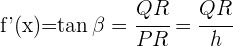
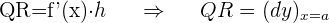
Das Differential an einem Punkt stellt den Zuwachs der Ordinate der Tangente dar, der einem Zuwachs der Variablen entspricht.

Aufgaben zu Differentialen
Berechne das Differential von 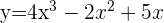
Berechne das Differential von 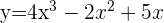
Wir berechnen die Ableitung der Funktion und addieren die Differentiale auf beiden Seiten der Gleichung
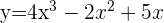
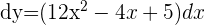
Berechne das Differential von 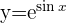
Berechne das Differential von 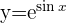
Wir berechnen die Ableitung der Funktion und addieren die Differentiale auf beiden Seiten der Gleichung
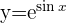
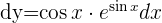
Berechne das Differential von 
Berechne das Differential von  Wir berechnen die Ableitung der Funktion und addieren die Differentiale auf beiden Seiten der Gleichung
Wir berechnen die Ableitung der Funktion und addieren die Differentiale auf beiden Seiten der Gleichung

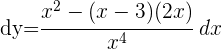
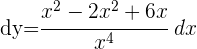

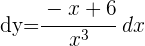
Anwendungsorientierte Aufgaben
Berechne den Flächenzuwachs eines Kreises mit dem Radius 3 cm, wenn sein Radius um 0,5 cm zunimmt.
Berechne den Flächenzuwachs eines Kreises mit einem Radius 3 cm, wenn sein Radius um 0,5 cm zunimmt.
1 Wir wissen, dass das Verhältnis zwischen der Fläche und dem Radius eines Kreises wie folgt ist:
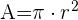
2 Wir berechnen das Differential von Volumen und Radius

3 Wir setzen r=3 cm und dr=0,5 cm ein
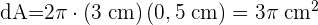
Ein Kegel mit einer Höhe von 5 m und einem Radius von 3 m an der Basis vergrößert seinen Radius um 0,25 m, während seine Höhe konstant bleibt. Berechne den Zuwachs seines Volumens
Ein Kegel mit einer Höhe von 5 m und einem Radius von 3 m an der Basis vergrößert seinen Radius um 0,25 m, während seine Höhe konstant bleibt. Berechne den Zuwachs seines Volumens
1 Wir wissen, dass das Volumen eines Kegels wie folgt gegeben ist:
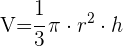
2 Wir berechnen das Differential von Volumen und Radius

3 Wir setzen r=3 m, h=5 m und dr=0,25 m ein
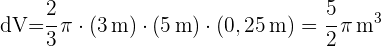
Ein Würfel hat eine Kantenlänge von 10 cm. Um wie viel muss die Kante vergrößert werden, damit sein Volumen um 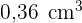 zunimmt?
zunimmt?
Ein Würfel hat eine Kantenlänge von 10 cm. Um wie viel muss die Kante vergrößert werden, damit sein Volumen um 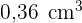 zunimmt?
zunimmt?
1 Wir wissen, dass das Volumen eines Würfels wie folgt gegeben ist:

2 Wir berechnen das Differential von Volumen und Kante

3 Wir erhalten
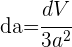
4 Wir setzen 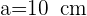 und
und 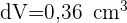 ein
ein
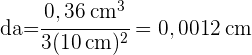
Das Volumen einer Metallkugel nimmt um 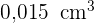 , wenn sie kalt wird. Ihr ursprünglicher Radius betrug 3 cm. Berechne die Abnahmes ihres Radius.
, wenn sie kalt wird. Ihr ursprünglicher Radius betrug 3 cm. Berechne die Abnahmes ihres Radius.
Das Volumen einer Metallkugel nimmt um 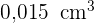 , wenn sie kalt wird. Ihr ursprünglicher Radius betrug 3 cm. Berechne die Abnahmes ihres Radius.
, wenn sie kalt wird. Ihr ursprünglicher Radius betrug 3 cm. Berechne die Abnahmes ihres Radius.
1 Wir wissen, dass das Volumen einer Kugel wie folgt gegeben ist:

2 Wir berechnen das Differenzial von Volumen und Radius
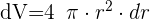
3 Wir berechnen dr
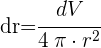
4 Wir setzen 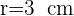 und
und 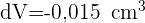 ein
ein
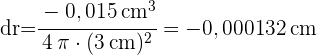
Beim Aufblasen eines kugelförmigen Ballons vergrößert sich der Radius mit einem Atemzug um 0,0035 cm, wenn der Ballon 4 cm misst. Um wie viel hat sich das Volumen vergrößert?
Beim Aufblasen eines kugelförmigen Ballons vergrößert sich der Radius mit einem Atemzug um 0,0035 cm, wenn der Ballon 4 cm misst. Um wie viel hat sich das Volumen vergrößert?
1 Wir wissen, dass das Volumen einer Kugel gegeben ist durch:

2 Wir berechnen das Differential von Volumen und Radius
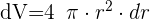
3 Wir setzen r=4 cm und dr=0,0035 cm ein
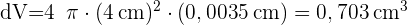
Um wie viel steigt der Wert von „y“, wenn der Wert von „x“ um 0,45 Einheiten in der Funktion 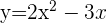 , steigt, wenn x=5?
, steigt, wenn x=5?
1 Wir berechnen das Differential der Funktion 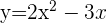

2 Wir setzen  und
und 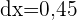 ein
ein
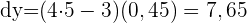
Um wie viel vergrößert sich das Volumen eines Kegels mit einer Höhe von 4 cm und einem Radius von 2 cm, wenn seine Grundfläche konstant bleibt und seine Höhe um 0,75 cm zunimmt?
Um wie viel vergrößert sich das Volumen eines Kegels mit einer Höhe von 4 cm und einem Radius von 2 cm, wenn seine Grundfläche konstant bleibt und seine Höhe um 0,75 cm zunimmt?
1 Wir wissen, dass das Volumen eines Kegels gegeben ist durch:
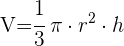
2 Wir berechnen das Differential unter der Annahme, dass der Radius konstant bleibt.
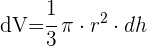
3 Wir setzen r=2 cm und dh=0,75 cm ein
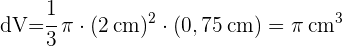
Mit KI zusammenfassen:












