Kapitel

Aufgaben mit Lösungen
Ermittle die Intervalle, auf denen die Funktion 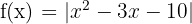 steigt oder fällt
steigt oder fällt
1 Wir schreiben den Betrag als abschnittsweise definierte Funktion
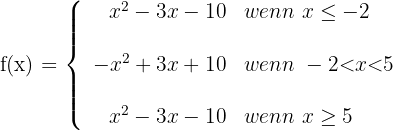
Wir leiten die Funktion ab
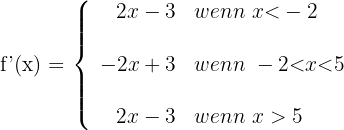
2 Wir berechnen die Nullstellen der 1. Ableitung, dazu setzen wir die Ableitung gleich 0 und lösen nach  . Für jeden Teil der Funktion gilt:
. Für jeden Teil der Funktion gilt:
wenn 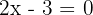 für
für 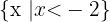 , ist
, ist 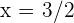 . Dieser Wert gehört jedoch nicht zu
. Dieser Wert gehört jedoch nicht zu 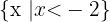 ; somit hat
; somit hat  keine Nullstellen auf
keine Nullstellen auf 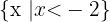
wenn  für
für 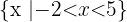 , ist
, ist 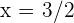 . Dies gehört zu
. Dies gehört zu 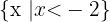 ; somit hat
; somit hat  eine Nullstelle auf
eine Nullstelle auf 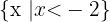
wenn 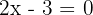 für
für 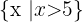 , ist
, ist 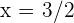 . Dieser Wert gehört jedoch nicht zu
. Dieser Wert gehört jedoch nicht zu 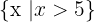 ; somit hat
; somit hat  keine Nullstellen auf
keine Nullstellen auf 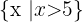
An den Punkten  und
und 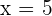 hingegen existiert die Ableitung nicht, so dass wir die seitlichen Grenzwerte für die Ableitung an diesen Punkten berechnen.
hingegen existiert die Ableitung nicht, so dass wir die seitlichen Grenzwerte für die Ableitung an diesen Punkten berechnen.
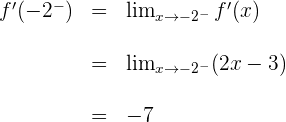
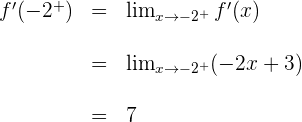
Da die seitlichen Ableitungen nicht übereinstimmen, gibt es die Ableitung 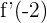 nicht. Auf die gleiche Weise führen wir die Berechnung für
nicht. Auf die gleiche Weise führen wir die Berechnung für 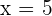 durch.
durch.

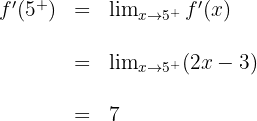
Da die seitlichen Ableitungen nicht übereinstimmen, gibt es die Ableitung 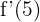 nicht.
nicht.
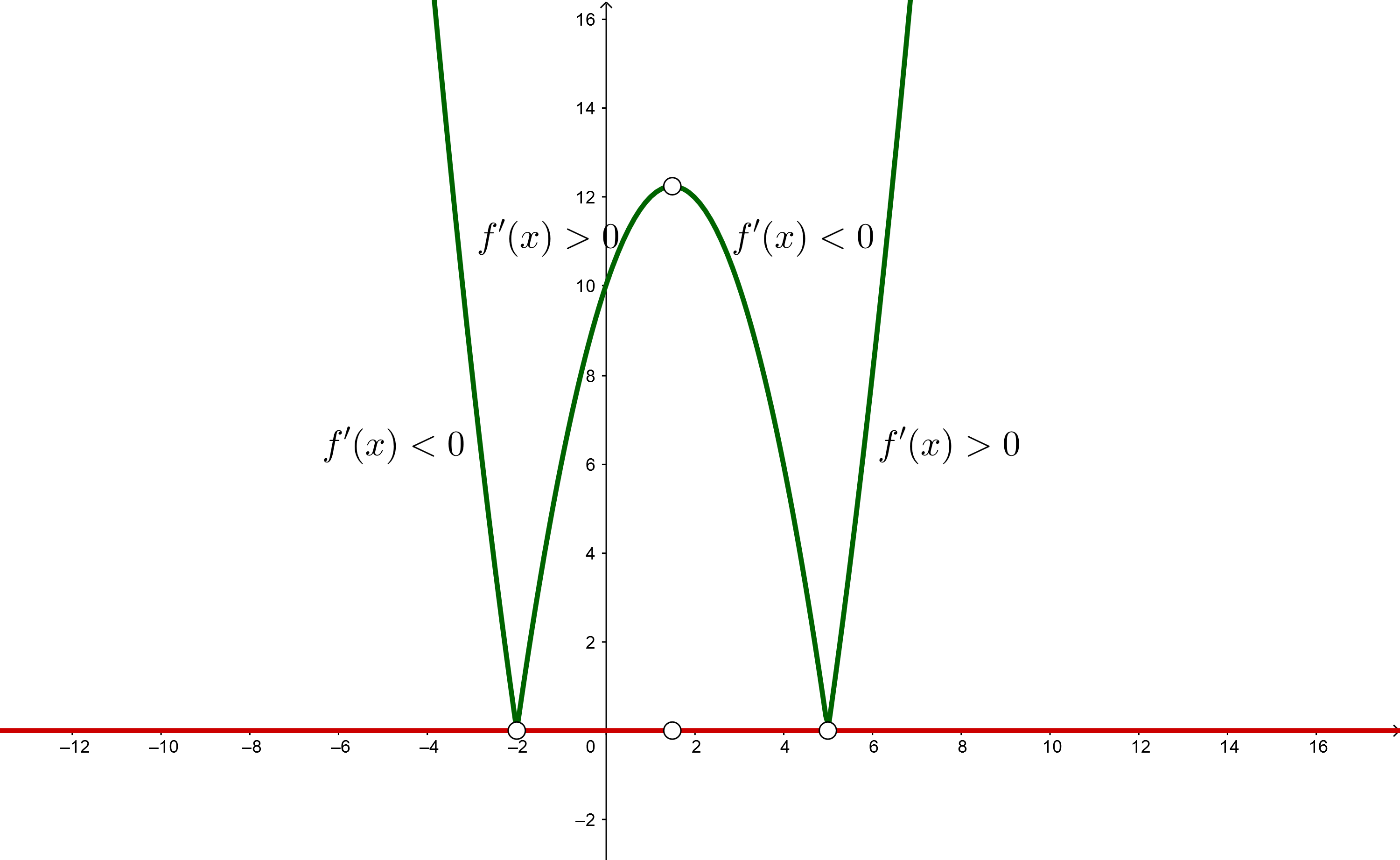
3 Wir bilden offene Intervalle mit den Nullstellen der 1. Ableitung und den Punkten, an denen es die Ableitung nicht gibt. Wir stützen uns dabei auf die Darstellung der Punkte auf der Zahlengeraden.
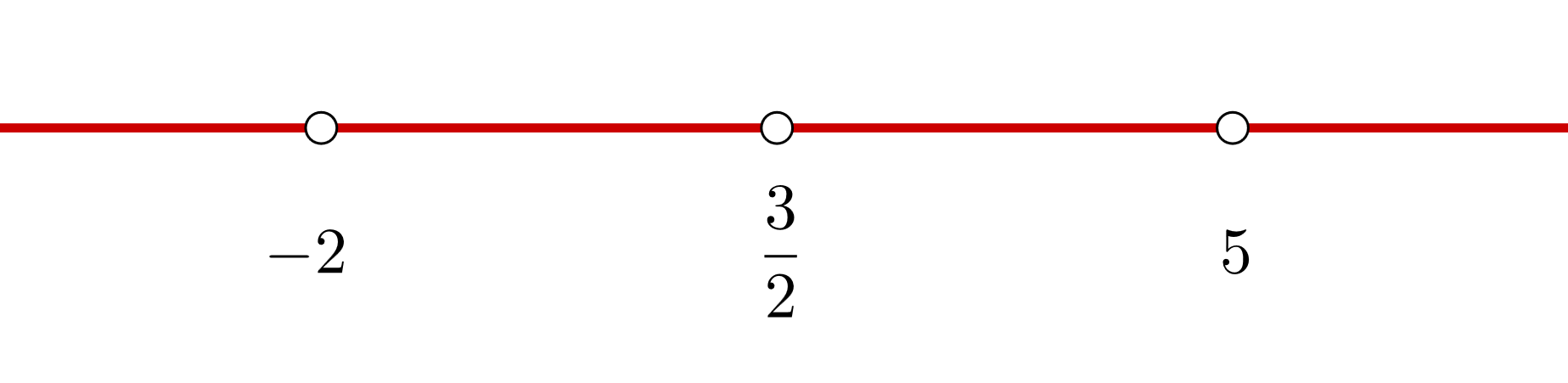
Die Intervalle, die wir erhalten, sind  und
und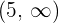
4 Wir nehmen einen Wert aus jedem Intervall (du kannst jeden Wert im Intervall nehmen) und bestimmen das Vorzeichen, das er in der 1. Ableitung hat.
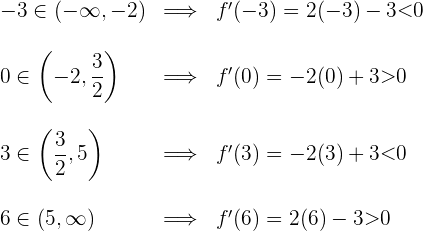
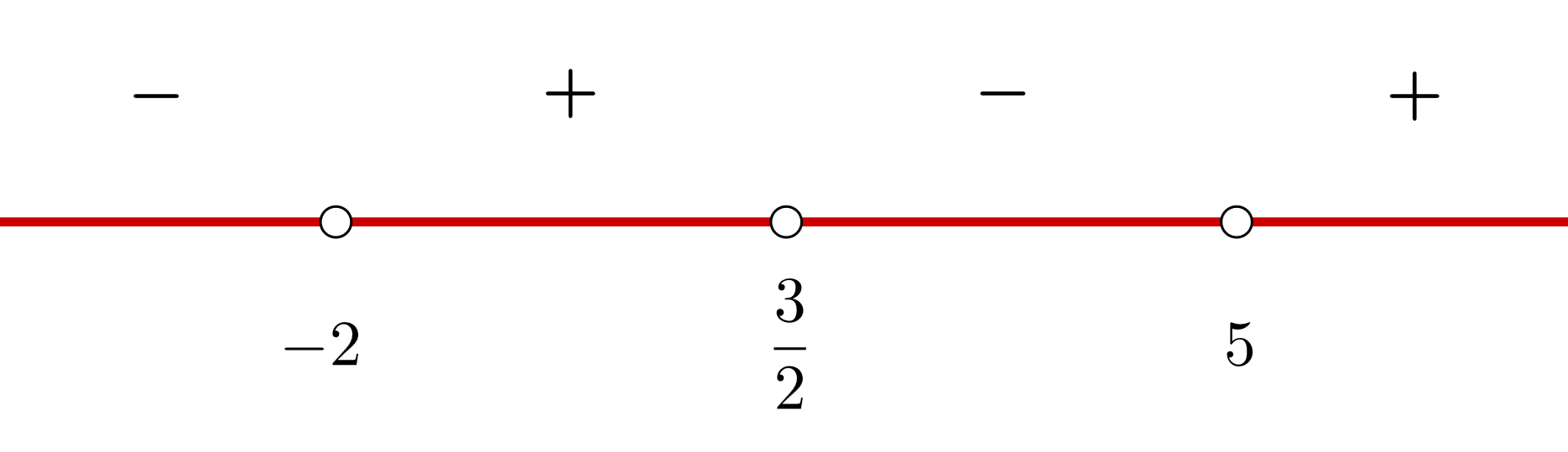
5 Wir schreiben die Intervalle, auf denen die Funktion steigt und fällt
Steigend: 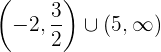
Fallend: 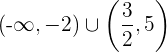
Ermittle die Intervalle, auf denen die Funktion  steigt oder fällt
steigt oder fällt
1 Wir leiten die Funktion ab

2 Wir berechnen die Nullstellen der 1. Ableitung (sofern vorhanden). Hierfür setzen wir die Ableitung gleich 0 und lösen nach  auf
auf

Wendet man die allgemeine Formel für quadratische Gleichungen auf den Zähler an, so hebt sich die obige Gleichung bei 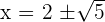 auf. Wir stellen fest, dass die Funktion und ihre Ableitung eine Unstetigkeitsstelle bei
auf. Wir stellen fest, dass die Funktion und ihre Ableitung eine Unstetigkeitsstelle bei  haben.
haben.
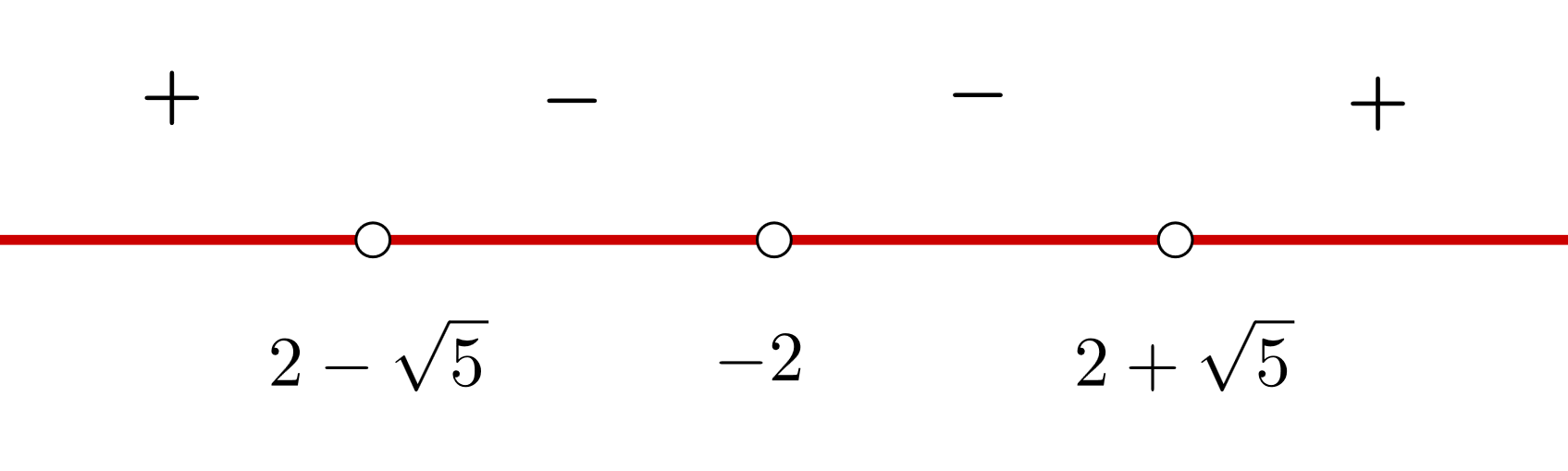
3 Wir bilden offene Intervalle mit der Unstetigkeitsstelle und den Nullstellen der Ableitung. Wir stützen uns auf die Darstellung der Punkte auf Zahlengeraden
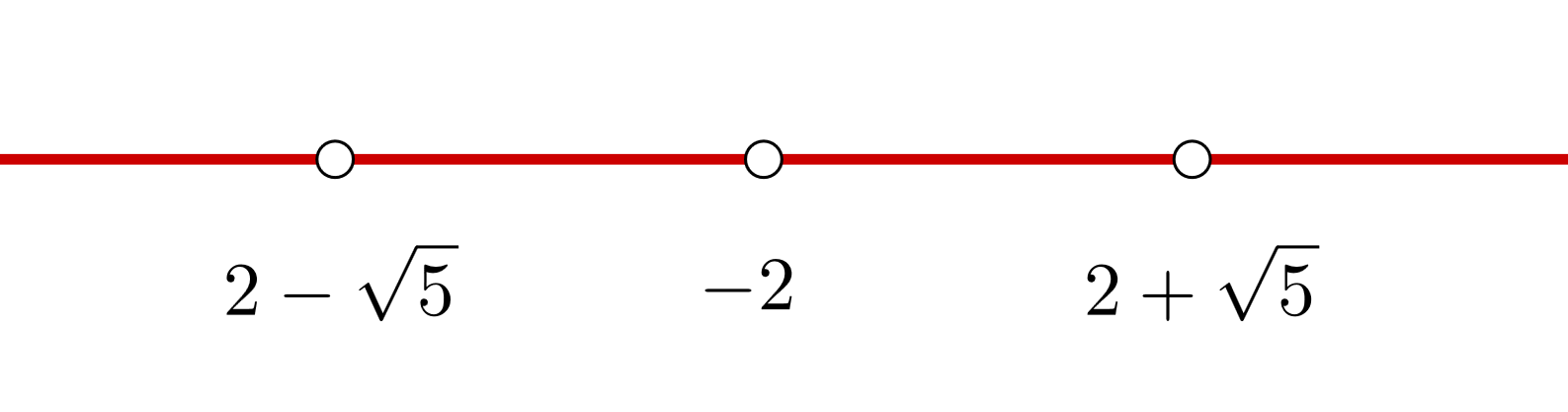
Die Intervalle, die wir erhalten, sind 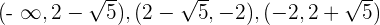 und
und 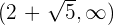
4 Wir nehmen einen Wert aus jedem Intervall (du kannst jeden Wert im Intervall nehmen) und bestimmen das Vorzeichen, das er in der 1. Ableitung hat.
Für das Intervall  nehmen wir
nehmen wir  , setzen in die Ableitung ein und erhalten
, setzen in die Ableitung ein und erhalten
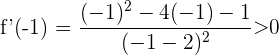
Für das Intervall  nehmen wir
nehmen wir  , setzen in die Ableitung ein und erhalten
, setzen in die Ableitung ein und erhalten
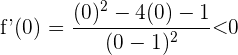
Für das Intervall  nehmen wir
nehmen wir  , setzen in die Ableitung ein und erhalten
, setzen in die Ableitung ein und erhalten
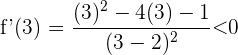
Für das Intervall 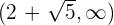 nehmen wir
nehmen wir  , setzen in die Ableitung ein und erhalten
, setzen in die Ableitung ein und erhalten
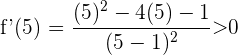
5 Wir schreiben die Intervalle, auf denen die Funktion steigt und fällt
Steigend: 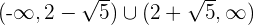
Fallend: 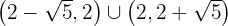
Bestimme die Intervalle, auf denen die Funktion mit Spitze 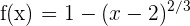 steigt und fällt
steigt und fällt
1 Wir leiten die Funktion ab

2 Wir berechnen die Nullstellen der 1. Ableitung (sofern vorhanden) und setzen hierfür die Ableitung gleich 0. Wir lösen nach  auf
auf
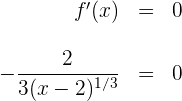
für  existieren keine Werte in den reellen Zahlen, die die vorherige Gleichung erfüllen. Somit hat die Ableitung keine Nullstellen. Wir stellen fest, dass die Ableitung bei
existieren keine Werte in den reellen Zahlen, die die vorherige Gleichung erfüllen. Somit hat die Ableitung keine Nullstellen. Wir stellen fest, dass die Ableitung bei  nicht existiert.
nicht existiert.
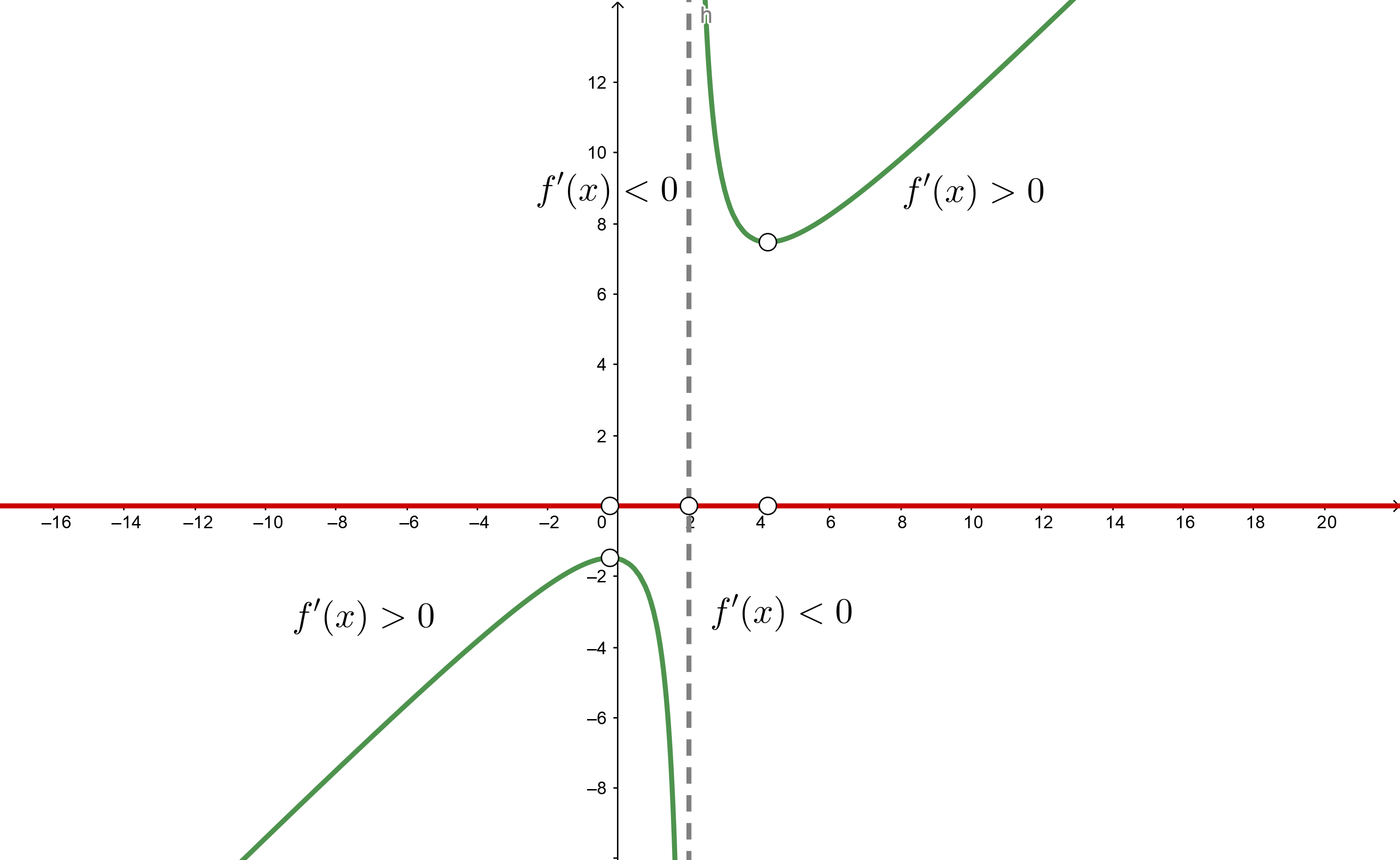
3 Wir bilden offene Intervalle mit der Unstetigkeitsstelle, in diesem Fall hat die Ableitung keine Nullstellen. Wir stützen uns auf die Darstellung der Punkte auf der Zahlengeraden.
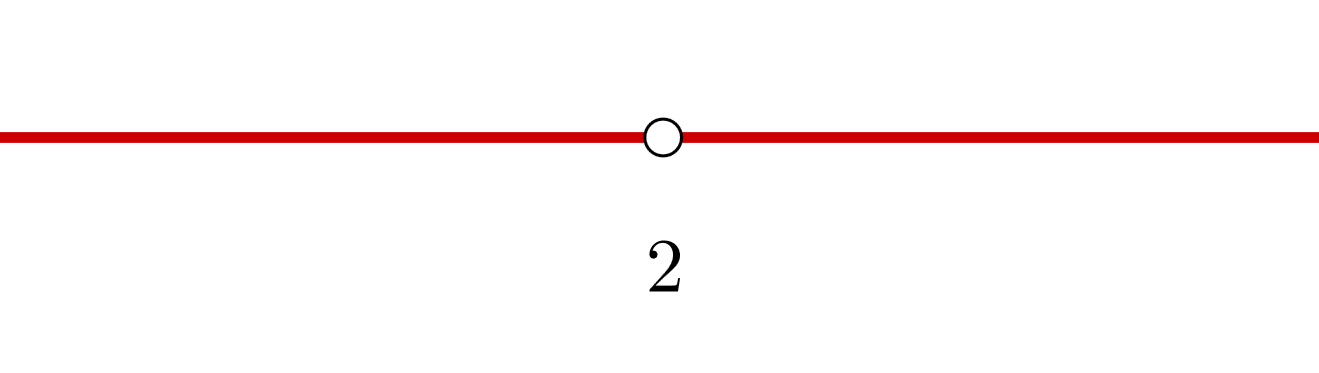
Die Intervalle, die wir erhalten, sind  y
y 
4 Wir nehmen einen Wert aus jedem Intervall (du kannst jeden beliebigen Wert nehmen) und ermitteln das Vorzeichen, das er in der 1. Ableitung hat.
Für das Intervall  nehmen wir
nehmen wir  , setzen in die Ableitung ein und erhalten
, setzen in die Ableitung ein und erhalten
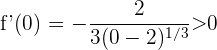
Für das Intervall 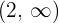 nehmen wir
nehmen wir  , setzen in die Ableitung ein und erhalten
, setzen in die Ableitung ein und erhalten
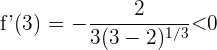
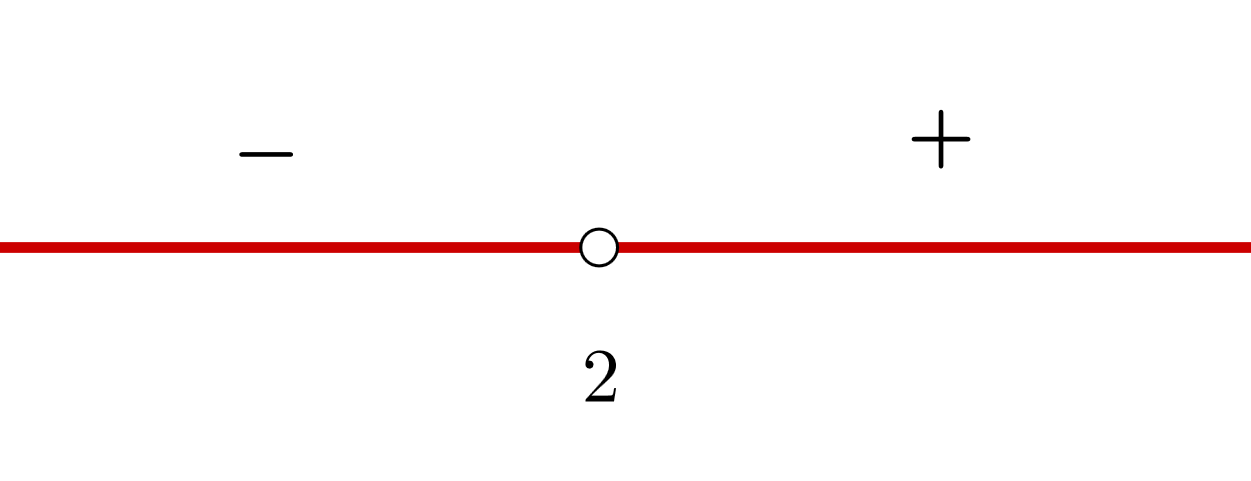
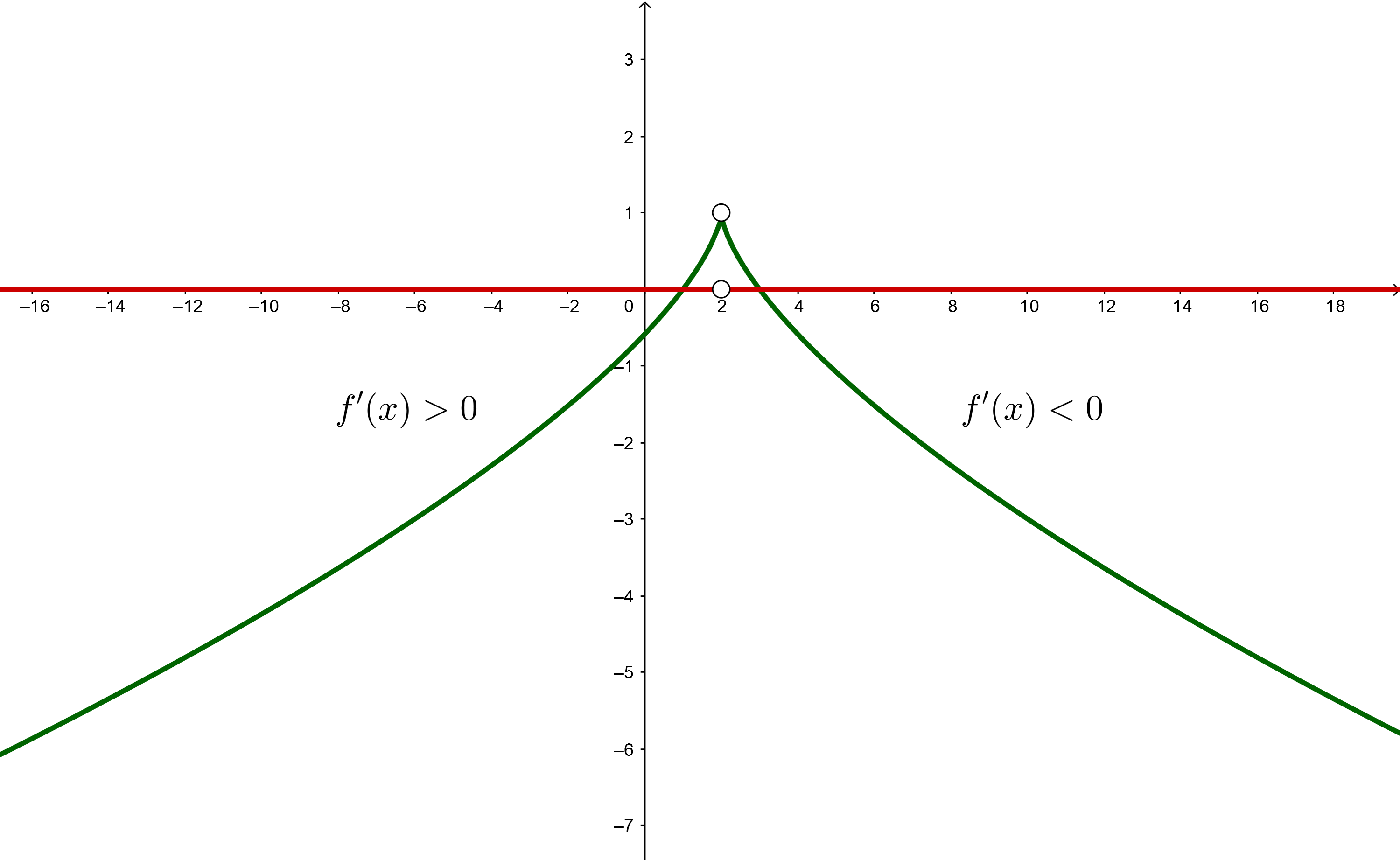
5 Wir schreiben die Intervalle, auf denen die Funktion steigt und fällt
Steigend: 
Fallend: 
Ermittle die Intervalle, auf denen die Funktion  steigt oder fällt
steigt oder fällt
1 Wir leiten die Funktion ab

2 Wir berechnen die Nullstellen der 1. Ableitung (sofern vorhanden). Hierfür setzen wir die Ableitung gleich 0 und lösen nach  auf
auf
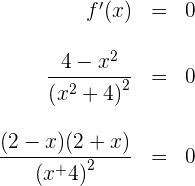
Die vorherige Gleichung hebt sich auf bei 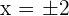 . Wir stellen fest, dass der Nenner der Gleichung niemals 0 ist.
. Wir stellen fest, dass der Nenner der Gleichung niemals 0 ist.
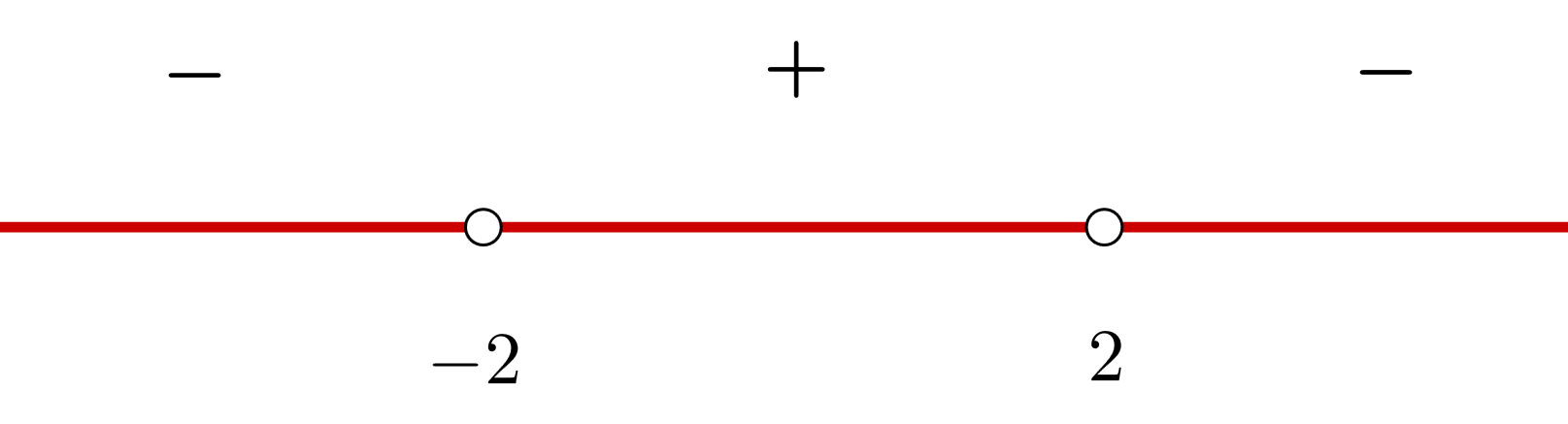
3 Wir bilden offene Intervalle mit den Nullstellen der Ableitung und stützen uns auf die Darstellung der Punkt auf der Zahlengeraden.

Die Intervalle, die wir erhalten, sind 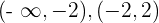 und
und 
4 Wir nehmen einen Wert auf jedem Intervall (du kannst jeden Wert im Intervall nehmen) und bestimmen das Vorzeichen, das er in der 1. Ableitung hat.
Für das Intervall 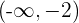 nehmen wir
nehmen wir  , setzen in die Ableitung ein und erhalten
, setzen in die Ableitung ein und erhalten
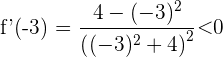
Für das Intervall  tomamos
tomamos  , setzen in die Ableitung ein und erhalten
, setzen in die Ableitung ein und erhalten
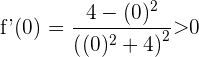
Für das Intervall 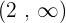 nehmen wir
nehmen wir  , setzen in die Ableitung ein und erhalten
, setzen in die Ableitung ein und erhalten
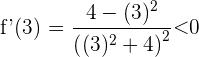
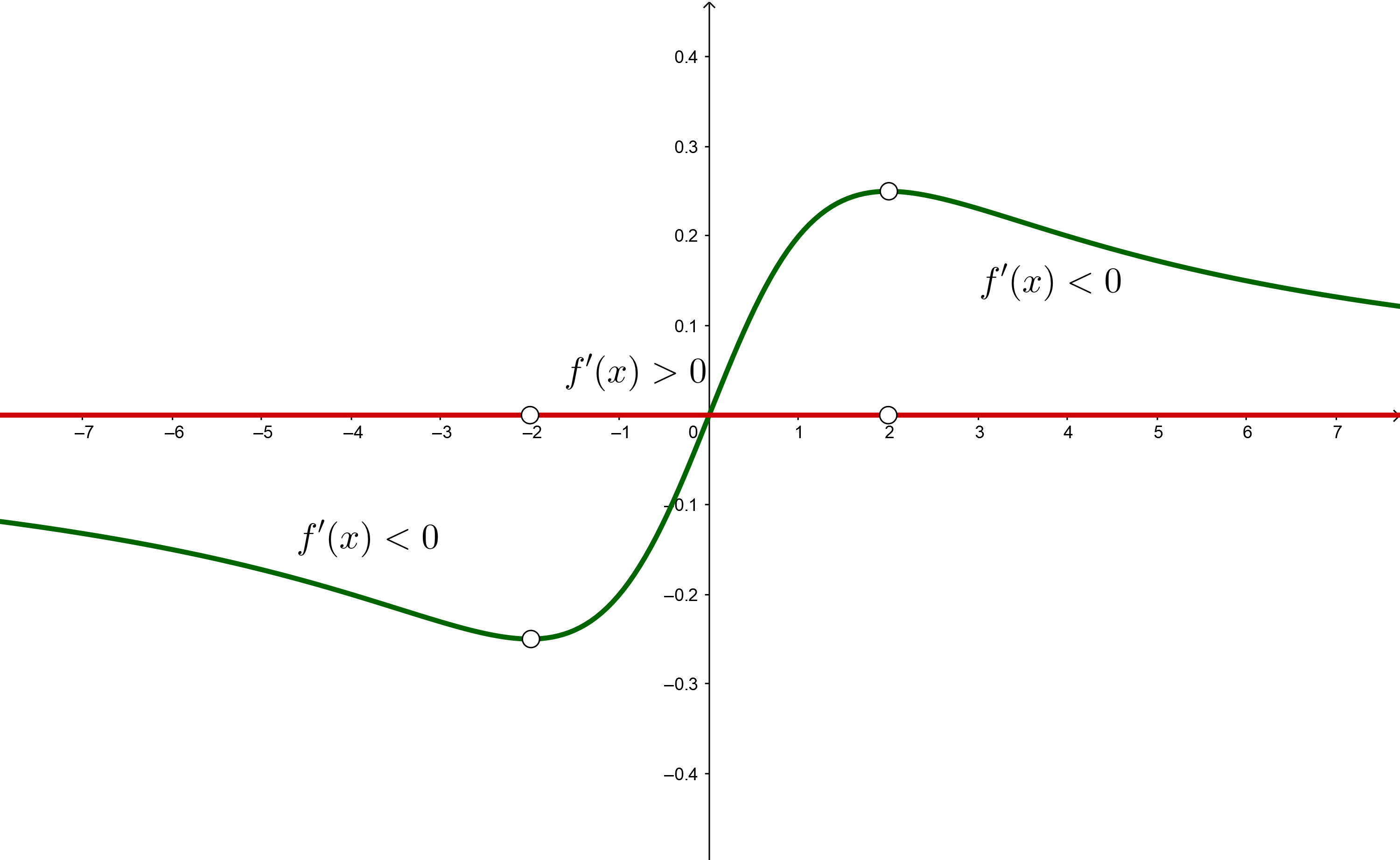
5 Wir schreiben die Intervalle, auf denen die Funktion steigt und fällt
Steigend: 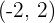
Fallend: 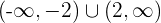
Bestimme die Werte von  , so dass die Funktion
, so dass die Funktion 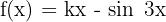 streng monoton steigt.
streng monoton steigt.
1 Wir leiten die Funktion ab
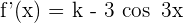
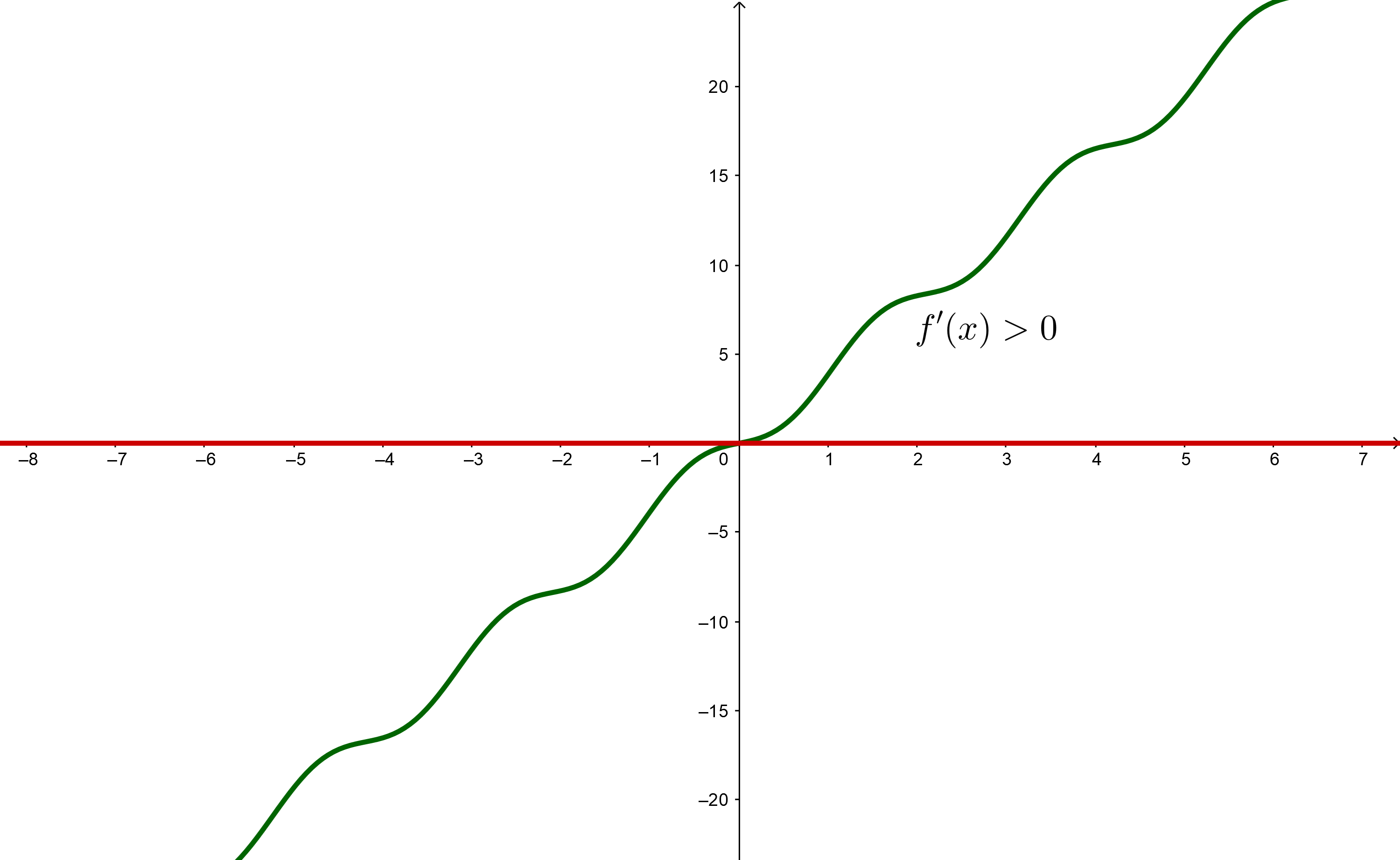
2 Damit die Funktion streng monoton steigt, muss die Ableitung größer als 0 sein.
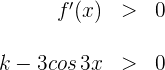
Wir wissen, dass 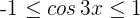 und somit
und somit 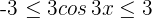 .
.
Wähle einfach  , um sicherzustellen, dass
, um sicherzustellen, dass 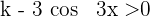 für jeden Wert
für jeden Wert 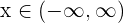
Mit KI zusammenfassen:












