Kapitel

Was ist die Kettenregel?
Sehr oft treten Funktionen auf, die eine kompliziertere Struktur haben und abgeleitet werden müssen, wobei eine direkte Ableitung mit den üblichen Formeln nicht möglich ist.
Aus diesem Grund ist es nützlich, weitere Werkzeuge zu kennen und zu erkennen, wie man solche Funktionen ableiten kann.
Wenn wir uns auf komplexere Funktionen beziehen, sprechen wir von Funktionen, die aus der Zusammensetzung von zwei anderen Funktionen entstehen.
Wir haben folgende zwei Funktionen
Nun können wir eine neue Funktion bilden: 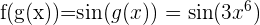 .
.
Wie lautet also die Ableitung der neuen Funktion  ?
?
Um diese Frage zu beantworten, müssen wir die folgende Formel verwenden
Formel der Kettenregel

Wie leiten wir mit der Kettenregel ab?
Die Kettenregel ermöglicht es, die Ableitung einer zusammengesetzten Funktion zu bestimmen, indem man die Ableitungen der Funktionen verwendet, aus denen sie zusammengesetzt ist. Der Ableitungsprozess ist sehr einfach und kann wie folgt durchgeführt werden (wir verwenden die oben genannte Funktion als Referenz):
- Wenn wir die Funktion
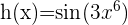 ableiten müssen, die sich aus der Zusammensetzung zweier anderer Funktionen
ableiten müssen, die sich aus der Zusammensetzung zweier anderer Funktionen 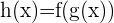 ergibt, müssen wir zunächst
ergibt, müssen wir zunächst 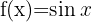 und
und  bestimmen
bestimmen - Sobald wir die Funktionen bestimmt haben, müssen wir
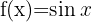 ableiten
ableiten
- Das Ergebnis der Ableitung von
 müssen wir mit
müssen wir mit  auswerten
auswerten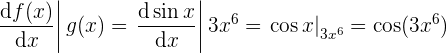
- Nun leiten wir
 ab
ab
- Schließlich multiplizieren wir die zwei Ergebnisse, um die Ableitung von
 zu erhalten
zu erhalten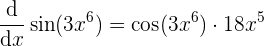
Mit diesem Verfahren können wir nun die gewünschte Ableitung erhalten. Es ist wichtig zu erwähnen, dass es mit mehr Übung möglich ist, das Vorgehen schneller durchzuführen, wenn man die zu befolgenden Schritte erkannt hat.
Beispiele für Übungen mit der Kettenregel
1 Leite die Funktion 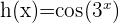 ab
ab
Wir gehen wie folgt vor:
- Wir bestimmen die Funktionen
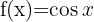 ,
, 
- Wir leiten
 ab
ab
- Wir werten das Ergebnis mit
 aus
aus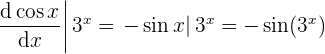
- Wir leiten
 ab
ab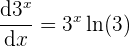
- Wir multiplizieren beide Ergebnisse
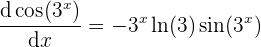
So erhalten wir bereits die Ableitung der Funktion  .
.
Es ist wichtig zu erwähnen, dass es gelegentlich nicht nur eine Zusammensetzung gibt, sondern mehrere. In diesem Fall ist die Kettenregel immer noch gültig, nur dass wir sie jetzt mehrmals anwenden, bis wir mit dem Ableiten fertig sind.
Auch dieser Vorgang wird auf einfache Art und Weise erarbeitet, ohne die konkreten Schritte zu beschreiben. Wichtig ist, dass wir die einzelnen Schritte üben.
2 Wir leiten die Funktion 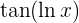 ab
ab
Zunächst bestimmen wir die Funktionen 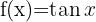 und
und 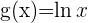 , damit wir die Kettenregel anwenden können:
, damit wir die Kettenregel anwenden können:
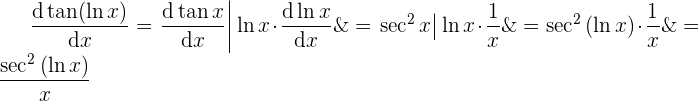
So erhalten wir bereits die Ableitung der Funktion 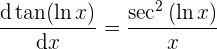
Beachte, dass bei der Ableitung die am Anfang genannten Schritte zum Einsatz kommen.
3 Wir leiten die Funktion 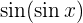 ab
ab
Wir bestimmen die Funktionen 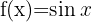 und
und 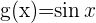 . Wie wir sehen können, ist dies nun weniger kompliziert, da die Ableitungen einfacher sind:
. Wie wir sehen können, ist dies nun weniger kompliziert, da die Ableitungen einfacher sind:
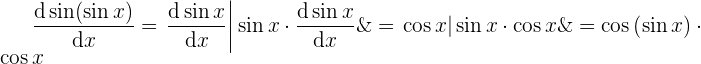
Wir erhalten das gesuchte Ergebnis.
4 Wir leiten die Funktion 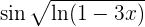 ab
ab
Hier stellen wir fest, dass es mehr als eine Zusammensetzung gibt. Um die Funktion ableiten zu können, müssen wir die Kettenregel mehrmals anwenden, bis wir mit dem Ableiten fertig sind.
Gehen wir zunächst von der Annahme aus, dass 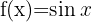 und
und 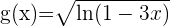 . Wir wenden also die Kettenregel an
. Wir wenden also die Kettenregel an 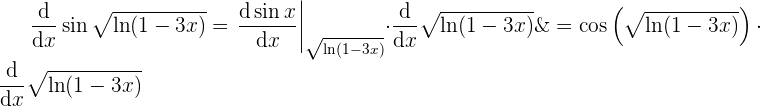
wir stellen damit fest, dass es nun notwendig ist, die Kettenregel für 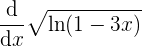 anzuwenden
anzuwenden
Wir wenden sie also an und addieren das Ergebnis zur ursprünglichen Ableitung 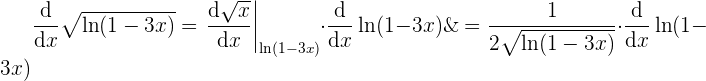
Nun sehen wir, dass wir erneut die Kettenregel anwenden müssen: 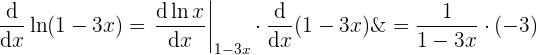
und damit können wir dann alle Ergebnisse vereinen 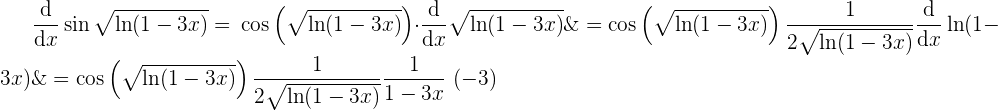
Daraus können wir schließen, dass 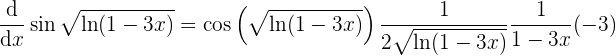
5 Leite die Funktion 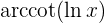 ab
ab
Wir bestimmen wieder die Funktionen  und
und 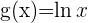 , sodass wir die Kettenregel anwenden können
, sodass wir die Kettenregel anwenden können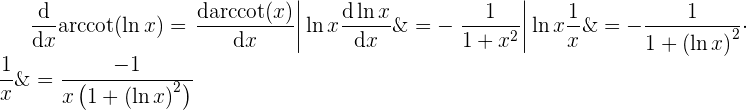 ,
,
Daraus schließen wir, dass 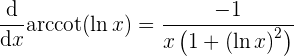
Mit KI zusammenfassen:












