Kapitel
Die Steigung der Tangente, die eine Kurve in einem Punkt tangiert
Für eine Gerade, die einen Graphen in einem Punkt tangiert, ist ihre Steigung die Ableitung der Funktion in diesem Punkt und wird wie folgt ausgedrückt:
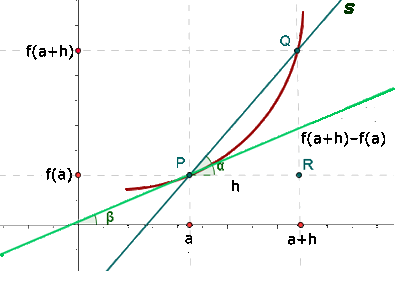
Die Tangente an einen Graphen in einem Punkt
Ebenso ist die Tangente an einen Graphen in einem Punkt diejenige, die durch den Punkt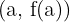 
verläuft und deren Steigung gleich 
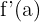ist. Sobald die Steigung der Geraden und die Punkte, durch die sie verläuft, bekannt sind, lautet ihre Gleichung:
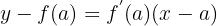
Beispiel für die Gleichung der Tangente
Ermittle die Gleichung der Tangente an die Parabel 
, die parallel zur Geraden 
verläuft.
1. Schritt: Wir ermitteln das 
in der Gleichung wie folgt:
2. Schritt: Mit den oben beschriebenen Informationen wissen wir, dass die Steigung der Geraden die Ableitung der vorherigen Funktion ist, die ihrem Koeffizienten entspricht:
3. Schritt: Ausgehend von den obigen Ausführungen müssen die beiden parallelen Geraden die gleiche Steigung haben. Wenn wir also die Gleichung der Parabel ableiten, erhalten wir:
Die Geraden haben die gleiche Steigung:
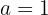
4. Schritt: Sobald der Wert der Koordinate 
bekannt ist, wird er in die Gleichung der Parabel eingesetzt, um die zweite Koordinate der Funktion zu ermitteln:
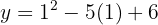
5. Schritt: Schließlich wenden wir die Punkt-Steigungsform an:
Da die Gerade parallel zum gegebenen Graphren verläuft, haben sie die gleiche Steigung.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
