Kapitel
Wir denken daran, dass die Logarithmusfunktion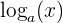 
als Umkehrfunktion des Exponenten 
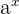definiert ist. Es gilt also folgende Beziehung:
Die Zahl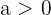 
ist die Basis des Exponenten. Wenn du hierzu mehr Infos haben möchtest, sieh dir unsere Seite zu Logarithmen an.
Ableitung des natürlichen Logarithmus
Wenn die Basis des Logarithmus die eulersche Zahl 
ist, wird der Logarithmus natürlicher Logarithmus (oder Napierscher Logarithmus oder Neperscher Logarithmus) genannt. In diesem Fall gilt
Wenn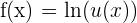 
, ist die Ableitung des natürlichen Logarithmus
,
wobei wir bereits die Kettenregel berücksichtigen.
Die Ableitung von 
ist
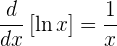
Ableitung eines Logarithmus mit beliebiger Basis
Wir wissen, dass der Logarithmus die folgende Eigenschaft erfüllt:
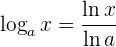
Wenn wir also den vorherigen Ausdruck ableiten, erhalten wir:
Die Ableitung des Logarithmus mit der Basis 
lautet somit
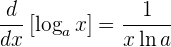
Wenn wir die Kettenregel berücksichtigen, dann ist die Ableitung
Hinweis: In vielen Fällen ist es besser, vor der Ableitung einige Gesetze der Logarithmen anzuwenden. Zum Beispiel:
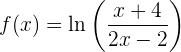
Wie wenden also das Gesetz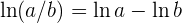 
an und erhalten:
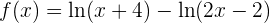
Auf diese Weise können wir die Anwendung der Quotientenregel für die Ableitungen vermeiden.
Aufgaben mit Lösungen
Berechne die Ableitung von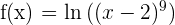 
Wir stellen fest, dass wir hier eine Potenz haben. Obwohl es einfach ist,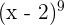 
abzuleiten, können wir auch folgendes Gesetz anwenden:
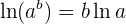
Die Funktion kann also auch wie folgt geschrieben werden:
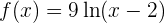
Dann können wir einen etwas einfacheren Ausdruck ableiten. Zunächst nutzen wir die Linearität der Ableitung (wir klammern die Konstante aus):
Wir leiten nun ab (mit der Kettenregel, wobei 
):
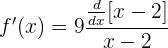
Die Ableitung von 
ist 1. Wir erhalten
,
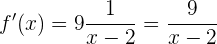welche unsere gesuchte Ableitung ist.
Berechne die Ableitung von
Bevor wir ableiten, wenden wir das 2. Logarithmusgesetz an
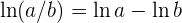
Die Funktion kann auch wie folgt geschrieben werden
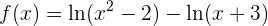
Nun leiten wir ab:
Wir wenden die Linearität der Ableitungen an:
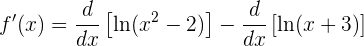
Und nun leiten wir jeden Ausdruck ab:
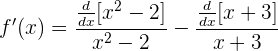
Da 
und 
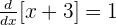, erhalten wir
,
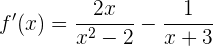welche unsere gesuchte Ableitung ist.
Berechne die Ableitung von
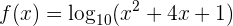
Wir denken daran, dass die Ableitung eines Logarithmus mit einer anderen Basis als etwas anders ist. Deshalb
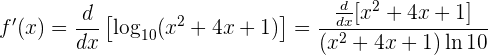
Außerdem haben wir 
. Die Ableitung lautet also
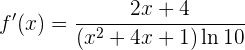
Berechne die Ableitung von
Um diese Ableitung zu ermitteln, lohnt es sich zunächst, die Gesetze von Logarithmen zu nutzen. Zunächst einmal
Da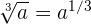 
, können wir die Funktion wie folgt schreiben
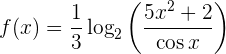
Nun wenden wir das Gesetz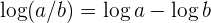 
an, um die Funktion wie folgt zu schreiben
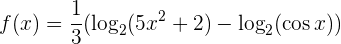
Und schon können wir die Funktion ableiten:
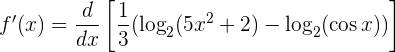
Wir wenden die Linearität der Ableitung an:
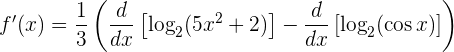
Nun leiten wir jeden Ausdruck ab:
Wir haben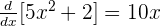 
und 
. Wir substituieren und erhalten
,
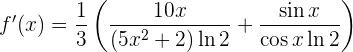welche die von uns gesuchte Ableitung ist.
Wende die implizite Ableitung an und berücksichtige die Tatsache, dass
,
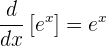um zu zeigen, dass
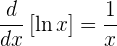
Wir beginnen mit unserer Funktion . Wir möchten zeigen, dass
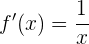
Dazu wenden wir die Exponentialfunktion auf beide Seiten an:
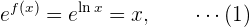
Nun wenden wir die implizite Ableitung bei diesem Ausdruck an
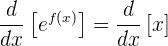
Die rechte Seite ist
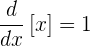
Die linke Seite ist
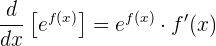
Wir erhalten also
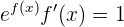
Wenn wir beide Seiten durch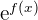 
dividieren, erhalten wir
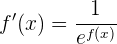
Bei (1) hatten wir jedoch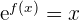 
, weshalb
.
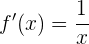Und genau das wollten wir beweisen.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
