In der Differentialrechnung ist der Mittelwertsatz eine Eigenschaft von ableitbaren Funktionen auf einem Intervall.
Aussage des Satzes
Der Satz besagt:
sei eine reelle Funktion 
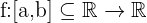. Wenn gilt:
1 ist stetig bei 
.
2 ist ableitbar bei 
(es existiert die Ableitung für jeden Punkt innerhalb von 
,
existiert ein Punkt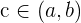 
, so dass
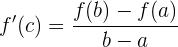
Kurz gesagt, es gibt mindestens einen Punkt, bei dem die Ableitung in diesem Punkt gleich der Steigung der Geraden, die die Punkte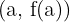 
und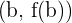 
verbindet, ist.
Geometrische Interpretation
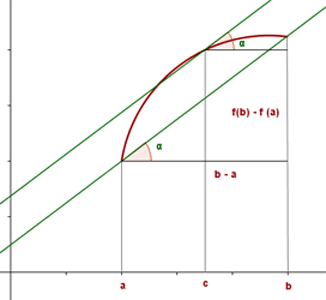
Die geometrische Interpretation des Mittelwertsatzes besagt, dass es einen Punkt gibt, in dem die Tangente parallel zur Sekante verläuft.
Satz von Rolle
Der Satz von Rolle ist ein besonderer Fall des Mittelwertsatzes, bei dem 
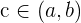. Wenn also eine Funktion den Mittelwertsatz erfüllt und außerdem , existiert ein Punkt , so dass
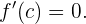
Beispiel
Kann der Mittelwertsatz auf die folgende Funktion im gegebenen Intervall angewendet werden?
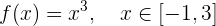
Wenn ja, ermittle den Wert von 
.
Der Mittelwertsatz kann angewendet werden, da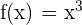 
stetig ist in 
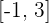und ableitbar ist in 
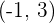. Da die Hypothese nun erfüllt ist, existiert ein Wert 
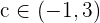. Um fortzufahren, berechnen wir nun die Ableitung von
Damit können wir nun fortfahren und ermitteln.
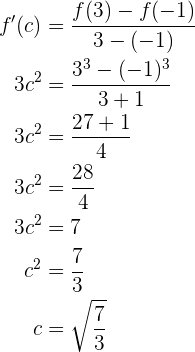
Wir nehmen die positive Wurzel 
, die negative Wurzel nicht, da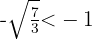 
und sich dieser Wert außerhalb des Intervalls befindet.
Kann der Mittelwertsatz auf die folgende Funktion im gegebenen Intervall angewendet werden?
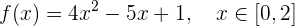
Wenn ja, ermittle den Wert von .
Der Mittelwertsatz kann in der Tat angewendet werden, da jedes Polynom auf jedem geschlossenen Intervall stetig und auf jedem offenen Intervall ableitbar ist. Da die Hypothese nun erfüllt ist, existiert ein Wert 
. Um fortzufahren, berechnen wir nun die Ableitung von
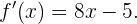
Damit können wir nun fortfahren und ermitteln.
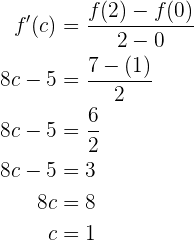
Kann der Mittelwertsatz auf die folgende Funktion im gegebenen Intervall angewendet werden?
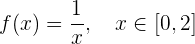
Wenn ja, ermittle den Wert von .
Die Funktion ist in 
nicht definiert, da wir eine Division durch 0 hätten. Also ist die Funktion nicht stetig in 
und somit erfüllt die Hypothese nicht. Daher können wir nicht garantieren, dass es irgendeinen Punkt gibt, der mit dem Ergebnis übereinstimmt.
Berechne einen Punkt auf dem Intervall 
, in dem die Tangente an den Graphen
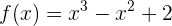
parallel zur Geraden ist, die durch die Punkte 
und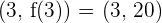 
bestimmt ist. Welcher Satz garantiert die Existenz dieses Punktes?
Damit zwei Geraden parallel sind, müssen sie die gleiche Steigung haben. Wir brauchen also die Steigung der Geraden, die durch die gegebenen Punkte verläuft.
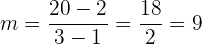
Nun berechnen wir die Ableitung von , die lautet
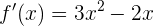
Um den Punkt zu finden, in dem die Tangente an den Graphen parallel zu der durch die gegebenen Punkte bestimmten Geraden verläuft, müssen wir die Ableitung mit der Steigung gleichsetzen und den Wert 
finden, der die Gleichheit erfüllt, d. h.
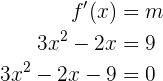
Um die Nullstellen zu bestimmen, können wir die quadratische Formel anwenden. Die Nullstellen sind
Jedoch gehört nur 
zum Intervall, weshalb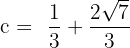 
der Punkt ist, den wir suchen.
Hätten wir nun die Existenz eines solchen Punktes sicherstellen können? Die Antwort ist ja. Wir beachten, dass ein Polynom ist, und jedes Polynom, das auf einem geschlossenen Intervall stetig und auf einem offenen Intervall ableitbar ist, zu den angenehmsten Funktionen gehört, die wir vorfinden können. Da die Hypothese des Mittelwertsatzes erfüllt, können wir die Existenz des Punktes sicherstellen.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
