Das Verhältnis zwischen der von einem Fahrzeug zurückgelegten Strecke in Metern und der Zeit in Sekunden ist  . Berechne:
. Berechne:
a Die Geschwindigkeit zwischen 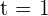 und
und  .
.
b Die Momentangeschwindigkeit bei 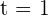 .
.
Das Verhältnis zwischen der von einem Fahrzeug zurückgelegten Strecke in Metern und der Zeit in Sekunden ist  . Berechne:
. Berechne:
a Die Geschwindigkeit zwischen 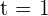 und
und  .
.
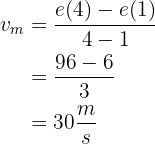
b Die Momentangeschwindigkeit bei 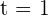 .
.
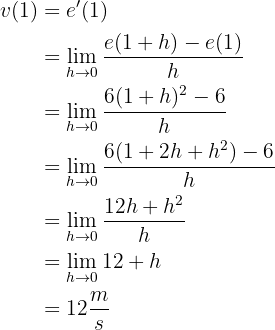
Aufgrund der schlechten Umweltbedingungen beginnt eine Kolonie von 1 Million Bakterien erst nach 2 Monaten mit der Vermehrung. Die Funktion, die die Population der Kolonie in Abhängigkeit von der Zeit (ausgedrückt in Monaten) darstellt, ist gegeben durch:
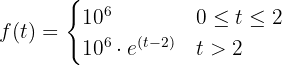
Es wird Folgendes verlangt:
a Überprüfe, ob die Population eine stetige Funktion der Zeit ist.
b Berechne die mittlere Änderungsrate der Population in den Intervallen  und
und  .
.
c Berechne die momentane Änderungsrate bei  .
.
Aufgrund der schlechten Umweltbedingungen beginnt eine Kolonie von einer Million Bakterien erst nach zwei Monaten mit der Vermehrung. Die Funktion, die die Grundgesamtheit der Kolonie in Abhängigkeit von der Zeit (ausgedrückt in Monaten) darstellt, ist gegeben durch:
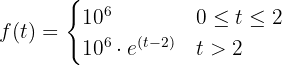
Es wird Folgendes verlangt:
a Überprüfe, ob die Population eine stetige Funktion der Zeit ist.
Der einzige Punkt, den wir untersuchen müssen liegt bei 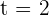 . Wir stellen fest, dass
. Wir stellen fest, dass
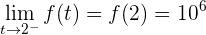 .
.
Außerdem
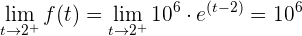 .
.
Sie ist also stetig.
b Berechne die mittlere Änderungsrate der Population in den Intervallen  und
und  .
.
Zunächst führen wir die Berechnungen für das Intervall  durch
durch
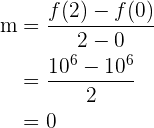 .
.
Nun berechnen wir für das Intervall 
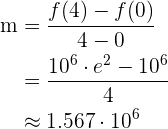 .
.
c Berechne die momentane Änderungsrate bei  .
.
Die Ableitung von 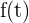 ist gegeben durch
ist gegeben durch
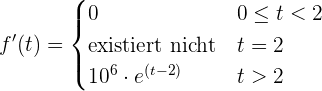 ,
,
weshalb
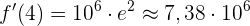
Eine Bakterienpopulation hat eine Wachstumsrate, die durch die Funktion 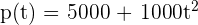 gegeben ist, wobei
gegeben ist, wobei 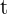 die Zeit in Stunden ist. Berechne:
die Zeit in Stunden ist. Berechne:
a Die mittlere Wachstumsgeschwindigkeit.
b Die momentane Wachstumsgeschwindigkeit.
c Die momentane Wachstumsgeschwindigkeit für 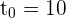 Stunden.
Stunden.
Eine Bakterienpopulation hat eine Wachstumsrate, die durch die Funktion 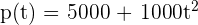 gegeben ist, wobei
gegeben ist, wobei 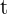 die Zeit in Stunden ist. Berechne:
die Zeit in Stunden ist. Berechne:
a Die mittlere Wachstumsgeschwindigkeit.
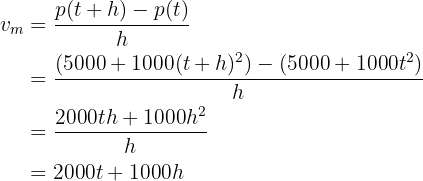
b Die momentane Wachstumsgeschwindigkeit.
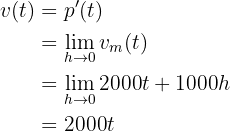
c Die momentane Wachstumsgeschwindigkeit für 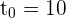 Stunden.
Stunden.
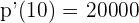
Die Gleichung für eine lineare Bewegung lautet:  . Zu welchem Zeitpunkt wird die Geschwindigkeit 0? Bestimme die Beschleunigung zu diesem Zeitpunkt.
. Zu welchem Zeitpunkt wird die Geschwindigkeit 0? Bestimme die Beschleunigung zu diesem Zeitpunkt.
Die Gleichung der linearen Bewegung lautet:  . Wir denken daran, dass die Geschwindigkeit die 1. Ableitung der Bewegungsfunktion ist. Um also den Zeitpunkt zu finden, an dem die Geschwindigkeit gleich 0 ist, müssen wir
. Wir denken daran, dass die Geschwindigkeit die 1. Ableitung der Bewegungsfunktion ist. Um also den Zeitpunkt zu finden, an dem die Geschwindigkeit gleich 0 ist, müssen wir 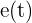 ableiten, gleich 0 setzen und nach
ableiten, gleich 0 setzen und nach 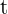 auflösen:
auflösen:
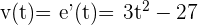 .
.
Wir setzen gleich  und lösen nach
und lösen nach 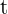 auf
auf
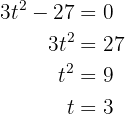
Wenn also 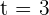 , ist die Geschwindigkeit null.
, ist die Geschwindigkeit null.
Die Beschleunigung ist gleich der Ableitung der Geschwindigkeit (oder der 2. Ableitung der Bewegung). Um also die Beschleunigung zu dem Zeitpunkt zu ermitteln, an dem die Geschwindigkeit 0 ist (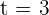 ), müssen wir
), müssen wir 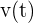 ableiten und bei
ableiten und bei 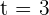 auswerten:
auswerten: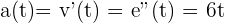 ,
,
Wir berechnen für 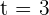 und erhalten
und erhalten
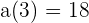 .
.
Die Gleichung für eine Kreisbewegung lautet: 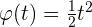 . Wie hoch sind die Winkelgeschwindigkeit und die Winkelbeschleunigung nach 7 Sekunden?
. Wie hoch sind die Winkelgeschwindigkeit und die Winkelbeschleunigung nach 7 Sekunden?
Die Gleichung für eine Kreisbewegung lautet: 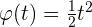 . Wie hoch sind die Winkelgeschwindigkeit und die Winkelbeschleunigung nach 7 Sekunden?
. Wie hoch sind die Winkelgeschwindigkeit und die Winkelbeschleunigung nach 7 Sekunden?
Wir wissen, dass die Geschwindigkeit die 1. Ableitung der Bewegungsfunktion ist. Um die Geschwindigkeit bei 7 Sekunden zu ermitteln, müssen wir also die Ableitung von  ermitteln und bei
ermitteln und bei  auswerten.
auswerten.
 .
.
Die Beschleunigung ist die 2. Ableitung der Bewegungsfunktion. Um die Beschleunigung nach 7 Sekunden zu erhalten, müssen wir also die Ableitung von  berechnen und bei
berechnen und bei  auswerten.
auswerten.
 .
.
Ein Beobachter befindet sich in einer Entfernung von  vom Start eines Raketenturms. Wenn die Rakete senkrecht abhebt, misst sie die Änderung des Winkels
vom Start eines Raketenturms. Wenn die Rakete senkrecht abhebt, misst sie die Änderung des Winkels 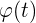 , den die Sichtlinie zwischen der Rakete und dem horizontalen Boden in Abhängigkeit von der verstrichenen Zeit bildet. Es ist bekannt, dass
, den die Sichtlinie zwischen der Rakete und dem horizontalen Boden in Abhängigkeit von der verstrichenen Zeit bildet. Es ist bekannt, dass 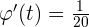 . Führe folgende Berechnungen durch:
. Führe folgende Berechnungen durch:
a In welcher Höhe befindet sich die Rakete im Bogenmaß 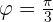 ?
?
b Wie hoch ist die Geschwindigkeit der Rakete im Bogenmaß 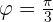 ?
?
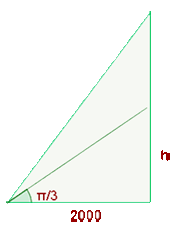
Ein Beobachter befindet sich in einer Entfernung von  vom Start eines Raketenturms. Wenn die Rakete senkrecht abhebt, misst sie die Änderung des Winkels
vom Start eines Raketenturms. Wenn die Rakete senkrecht abhebt, misst sie die Änderung des Winkels 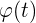 , den die Sichtlinie zwischen der Rakete und dem horizontalen Boden in Abhängigkeit von der verstrichenen Zeit bildet. Es ist bekannt, dass
, den die Sichtlinie zwischen der Rakete und dem horizontalen Boden in Abhängigkeit von der verstrichenen Zeit bildet. Es ist bekannt, dass 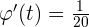 . Führe folgende Berechnungen durch:
. Führe folgende Berechnungen durch:
a In welcher Höhe befindet sich die Rakete im Bogenmaß 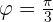 ?
?
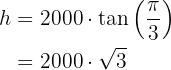
b Wie hoch ist die Geschwindigkeit der Rakete im Bogenmaß 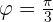 ?
?
Um die Geschwindigkeit zu ermitteln, müssen wir die Ableitung von 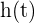 berechnen:
berechnen:
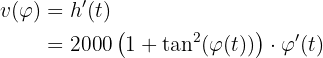
Somit
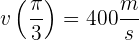
In einen kugelförmigen Ballon wird Gas mit einer Geschwindigkeit von 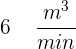 gepumpt. Der Druck bleibt dabei konstant. Wie schnell ändert sich der Radius des Ballons, wenn der Durchmesser
gepumpt. Der Druck bleibt dabei konstant. Wie schnell ändert sich der Radius des Ballons, wenn der Durchmesser 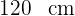 ist?
ist?
Zunächst berechnen wir 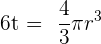 . Wenn wir also
. Wenn wir also 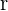 und
und 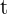 bestimmen, erhalten wir
bestimmen, erhalten wir
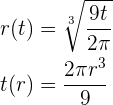
Wenn der Durchmesser 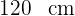 ist, misst der Radius
ist, misst der Radius 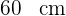 oder
oder 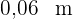 . Wenn wir
. Wenn wir 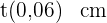 einsetzen, erhalten wir die Zeit
einsetzen, erhalten wir die Zeit
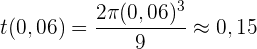
Wenn wir  bestimmen und
bestimmen und 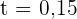 einsetzen, erhalten wir
einsetzen, erhalten wir
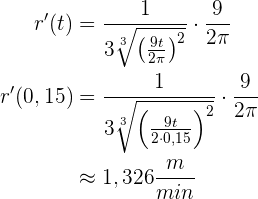
Wie hoch ist die Geschwindigkeit eines Fahrzeugs, das sich gemäß der Gleichung 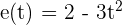 in der 5. Sekunde seiner Fahrt bewegt? Die Entfernung wird in Metern und die Zeit in Sekunden gemessen.
in der 5. Sekunde seiner Fahrt bewegt? Die Entfernung wird in Metern und die Zeit in Sekunden gemessen.
Wie hoch ist die Geschwindigkeit eines Fahrzeugs, das sich gemäß der Gleichung 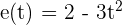 in der fünften Sekunde seiner Fahrt bewegt? Die Entfernung wird in Metern und die Zeit in Sekunden gemessen.
in der fünften Sekunde seiner Fahrt bewegt? Die Entfernung wird in Metern und die Zeit in Sekunden gemessen.
Die Geschwindigkeit ist durch die Ableitung  gegeben. Um also die Geschwindigkeit in der 5. Sekunde zu ermitteln, müssen wir
gegeben. Um also die Geschwindigkeit in der 5. Sekunde zu ermitteln, müssen wir  berechnen
berechnen
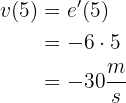
Mit KI zusammenfassen:


