
Satz von Rolle
Ist der Satz von Rolle auf die Funktion  auf dem Intervall
auf dem Intervall 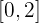 anwendbar?
anwendbar?
Ist der Satz von Rolle auf die Funktion  auf dem Intervall
auf dem Intervall 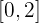 anwendbar?
anwendbar?
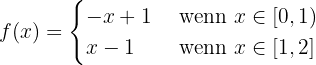
Die Funktion ist stetig bei 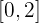 .
.
Der Satz von Rolle ist nicht anwendbar, weil die Lösung am Punkt  nicht ableitbar ist, da die Ableitungen in jeder Umgebung unterschiedliche Werte haben, und wenn sie ableitbar ist, sollten sie gleich sein.
nicht ableitbar ist, da die Ableitungen in jeder Umgebung unterschiedliche Werte haben, und wenn sie ableitbar ist, sollten sie gleich sein.
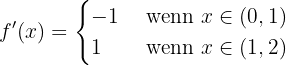
Untersuche, ob die Funktion 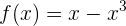 die Bedingungen des Satzes von Rolle auf den Intervallen
die Bedingungen des Satzes von Rolle auf den Intervallen  und
und  erfüllt, und wenn ja, bestimme die Werte von
erfüllt, und wenn ja, bestimme die Werte von  .
.
Untersuche, ob die Funktion 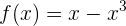 die Bedingungen des Satzes von Rolle in den Intervallen
die Bedingungen des Satzes von Rolle in den Intervallen  und
und  erfüllt, und wenn ja, bestimme die Werte von
erfüllt, und wenn ja, bestimme die Werte von  .
.
 ist eine stetige Funktion auf den Intervallen
ist eine stetige Funktion auf den Intervallen  und
und  und ableitbar auf den offenen Intervallen
und ableitbar auf den offenen Intervallen 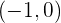 und
und 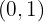 , da es sich um eine Polynomfunktion handelt.
, da es sich um eine Polynomfunktion handelt.
Además se cumple que:

Por tanto es aplicable el teorema de Rolle. Significa que ahora busquemos el punto donde la derivada de la función vale cero.
La derivada de la función es 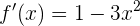 , entonces ahora valuamos en
, entonces ahora valuamos en
 e igualamos con cero, quedando la ecuación
e igualamos con cero, quedando la ecuación  , cuya solución es
, cuya solución es 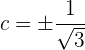 .
.
En otras palabras
 y
y 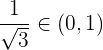
Erfüllt die Funktion 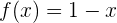 die Bedingungen des Satzes von Rolle auf dem Intervall
die Bedingungen des Satzes von Rolle auf dem Intervall 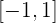 ?
?
Erfüllt die Funktion 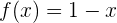 die Bedingungen des Satzes von Rolle auf dem Intervall
die Bedingungen des Satzes von Rolle auf dem Intervall 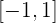 ?
?
Die Funktion ist stetig auf dem Intervall 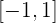 und ableitbar auf
und ableitbar auf  , da es sich um eine Polynomfunktion handelt.
, da es sich um eine Polynomfunktion handelt.
Allerdings ist der Satz von Rolle nicht erfüllt, da  .
.
Beweise, dass die Gleichung 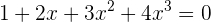 eine einzige Lösung in
eine einzige Lösung in 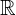 hat.
hat.
Beweise, dass die Gleichung 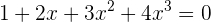 eine einzige Lösung in
eine einzige Lösung in 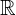 hat.
hat.
Wir beweisen dies durch den Widerspruchsbeweis.
Angenommen, die Funktion  hat zwei verschiedene Nullstellen
hat zwei verschiedene Nullstellen  und
und 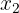 mit
mit  ableitbar ist, weil es sich um eine Polynomfunktion handelt, können wir den Satz von Rolle anwenden.
ableitbar ist, weil es sich um eine Polynomfunktion handelt, können wir den Satz von Rolle anwenden.
Daher existiert 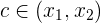 , so dass
, so dass 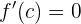 .
.
Wenn also  , haben wir
, haben wir 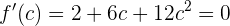 .
.
Mit anderen Worten:  ist eine reelle Nullstelle des Polynoms
ist eine reelle Nullstelle des Polynoms 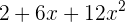 . Dies ist falsch, da es keine reellen Nullstellen zulässt, weil die Diskriminante negativ ist
. Dies ist falsch, da es keine reellen Nullstellen zulässt, weil die Diskriminante negativ ist  \displaystyle \bigtriangleup =(6)^2-4(12)(2)=36-96=-60<0[/latex]
\displaystyle \bigtriangleup =(6)^2-4(12)(2)=36-96=-60<0[/latex]
Da die Ableitung bei keinem Wert 0 wird, steht sie im Widerspruch zum Satz von Rolle, so dass die Hypothese, es gebe zwei Nullstellen, falsch ist.
Satz von Bolzano-Weierstraß
Wie viele reelle Nullstellen hat die Gleichung 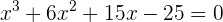 ?
?
Wie viele reelle Nullstellen hat die Gleichung 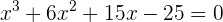 ?
?
Die Funktion 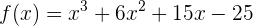 ist stetig und ableitbar im gesamten Bereich
ist stetig und ableitbar im gesamten Bereich 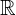
Wenn wir diese Eigenschaften kennen, können wir den Satz von Bolzano-Weierstraß anwenden. Dieser besagt, dass, wenn wir zwei reelle Nullstellen finden, bei denen die Funktion bei der Auswertung unterschiedliche Vorzeichen erhält, wir mindestens eine reelle Zahl haben, bei der die Funktion 0 wird.
Die vorgeschlagenen Werte sind 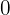 und
und 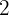 :
:
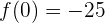

Daher hat die Gleichung mindestens eine Lösung auf dem Intervall 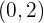 .
.
Andererseits stellen wir fest, dass otro lado observamos que  eine negative Diskriminante hat
eine negative Diskriminante hat 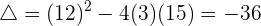 , d.h. sie ist nicht monoton steigend, daher ist der Wert, den wir ermitteln, für den die Funktion 0 wird, eindeutig.
, d.h. sie ist nicht monoton steigend, daher ist der Wert, den wir ermitteln, für den die Funktion 0 wird, eindeutig.
Zeige, dass die Gleichung 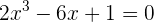 eine einzige reelle Lösung auf dem Intervall
eine einzige reelle Lösung auf dem Intervall 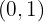 hat.
hat.
Zeige, dass die Gleichung 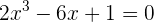 eine einzige reelle Lösung auf dem Intervall
eine einzige reelle Lösung auf dem Intervall 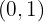 hat.
hat.
Die Funktion  ist stetig und ableitbar im gesamten Bereich
ist stetig und ableitbar im gesamten Bereich 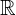 .
.
Das bedeutet, dass nach dem Satz von Bolzano-Weierstraß bei der Suche nach zwei Werten, bei denen die Funktion unterschiedliche Vorzeichen annimmt Folgendes gilt:

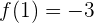
Wir können sagen, dass die Gleichung mindestens eine Lösung auf dem Intervall 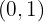 hat.
hat.
Nehmen wir nun ihre Ableitung  , stellen wir fest, dass sie 0 wird nos damos cuenta que ella se anula
, stellen wir fest, dass sie 0 wird nos damos cuenta que ella se anula  an den Punkten
an den Punkten  und
und  . Das heißt, das Maximum und das Minimum der Funktion liegt außerhalb von
. Das heißt, das Maximum und das Minimum der Funktion liegt außerhalb von 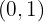 , so dass der Punkt, an dem die Funktion 0 wird, nur ein Punkt ist.
, so dass der Punkt, an dem die Funktion 0 wird, nur ein Punkt ist.
Wenn es zwei gibt, sollten die Maxima und Minima der Funktion innerhalb des Intervalls liegen, da die Funktion stetig ist.
Mittelwertsatz der Differentialrechnung
Kann der Mittelwertsatz (MWS) auf 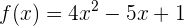 in
in 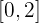 angewendet werden?
angewendet werden?
Kann der Mittelwertsatz (MWS) auf 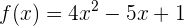 in
in 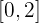 angewendet werden?
angewendet werden?
 ist stetig bei
ist stetig bei 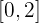 und ableitbar bei
und ableitbar bei 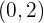 , weshalb der Mittelwertsatz angewendet werden kann.
, weshalb der Mittelwertsatz angewendet werden kann.
Daher existiert  , so dass
, so dass
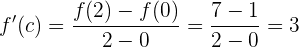
und wenn 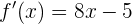 , hat die Gleichung
, hat die Gleichung  die Lösung
die Lösung 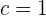 .
.
Kann der Mittelwertsatz (MWS) auf 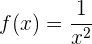 in
in 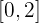 angewendet werden?
angewendet werden?
Kann der Mittelwertsatz (MWS) auf 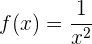 in
in 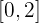 angewendet werden?
angewendet werden?
Nein, denn die Funktion ist nicht stetig bei 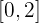 , da sie bei
, da sie bei  nicht definiert ist.
nicht definiert ist.
Wir nehmen den Abschnitt einer Parabel, der zwischen den Punkten 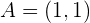 und
und  liegt. Finde einen Punkt, in dem die Tangente parallel zu der Strecke verläuft, die die Punkte
liegt. Finde einen Punkt, in dem die Tangente parallel zu der Strecke verläuft, die die Punkte  und
und 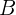 verbindet.
verbindet.
Wir nehmen den Abschnitt einer Parabel, der zwischen den Punkten 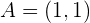 und
und  liegt. Finde einen Punkt, in dem die Tangente parallel zu der Strecke verläuft, die die Punkte
liegt. Finde einen Punkt, in dem die Tangente parallel zu der Strecke verläuft, die die Punkte  und
und 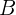 verbindet.
verbindet.
Die Punkte 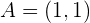 und
und  gehören zur Parabel der Gleichung
gehören zur Parabel der Gleichung 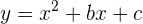 , so dass sich bei deren Auswertung das folgende Gleichungssystem ergibt
, so dass sich bei deren Auswertung das folgende Gleichungssystem ergibt
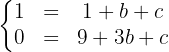
Die Lösung ist  .
.
Die Parabel hat also die Gleichung
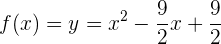
Da es sich um eine Polynomfunktion handelt, kann der Mittelwertsatz auf das Intervall 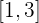 angewendet werden. Es existiert also
angewendet werden. Es existiert also 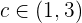 , so dass
, so dass
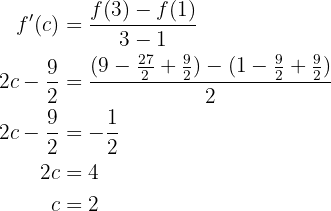
Jetzt werten wir einfach die Funktion aus, um den Punkt 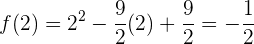 zu ermitteln.
zu ermitteln.
Somit ist der gesuchte Punkt 
Berechne einen Punkt auf dem Intervall 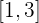 , in dem die Tangente an den Graphen
, in dem die Tangente an den Graphen  parallel zu der durch die Punkte
parallel zu der durch die Punkte 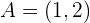 und
und 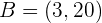 bestimmten Geraden verläuft. Welcher Satz garantiert die Existenz dieses Punktes?
bestimmten Geraden verläuft. Welcher Satz garantiert die Existenz dieses Punktes?
Berechne einen Punkt auf dem Intervall 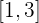 , in dem die Tangente an den Graphen
, in dem die Tangente an den Graphen  parallel zu der durch die Punkte
parallel zu der durch die Punkte 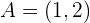 und
und 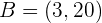 bestimmten Geraden verläuft. Welcher Satz garantiert die Existenz dieses Punktes?
bestimmten Geraden verläuft. Welcher Satz garantiert die Existenz dieses Punktes?
Wir ermitteln die Steigung der Geraden, die durch die beiden Punkte verläuft.
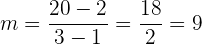
Wir dürfen nicht vergessen, dass der von uns berechnete Wert 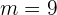 gleich der Steigung der Tangente ist, die den Graphen in diesem Punkt tangiert, da parallele Geraden dieselbe Steigung haben.
gleich der Steigung der Tangente ist, die den Graphen in diesem Punkt tangiert, da parallele Geraden dieselbe Steigung haben.
Da andererseits 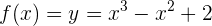 stetig in
stetig in 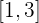 und ableitbar in
und ableitbar in 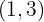 ist, kann der Mittelwertsatz angewendet werden:
ist, kann der Mittelwertsatz angewendet werden:
Daher existiert 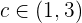 , so dass
, so dass
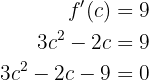
Die Lösung ist 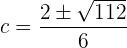 , woraus wir
, woraus wir  wählen, da es zum Intervall
wählen, da es zum Intervall 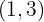 gehört
gehört
Bestimme  und
und  , so dass die Funktion
, so dass die Funktion
den Mittelwertsatz auf dem Intervall 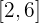 erfüllt.
erfüllt.
Bestimme  und
und  , so dass die Funktion
, so dass die Funktion
den Mittelwertsatz auf dem Intervall 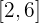 erfüllt.
erfüllt.
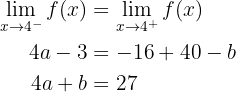
Wir erhalten die Gleichung 
Zweitens muss erfüllt sein, dass die Funktion ableitbar ist in 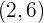
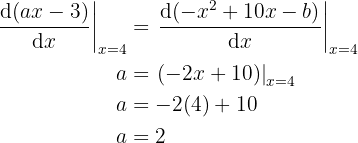
Das bedeutet, dass die Werte für die Erfüllung des Mittelwertsatzes (MWS) folgendermaßen sein müssen
 und
und 
Mit KI zusammenfassen:












