Der Satz von Rolle ist nach Michel Rolle (1652 - 1719), einem französischen Mathematiker, benannt. Rolle war einer der ersten Mathematiker, die an der Entwicklung der Infinitesimalrechnung arbeiteten, obwohl er zu den Kritikern der Grundlagen dieses Bereichs gehörte. Er ist auch einer der Erfinder des Gaußschen Eliminationsverfahrens.

Aussage des Satzes
Mit dem Satz von Rolle lässt sich feststellen, ob eine Funktion  einen kritischen Punkt in einem bestimmten Intervall hat. Dieser Satz wird wie folgt formuliert:
einen kritischen Punkt in einem bestimmten Intervall hat. Dieser Satz wird wie folgt formuliert:
Satz: Die Funktion  sei
sei
1 stetig bei 
2 ableitbar bei 
3 und erfüllt  .
.
Somit gibt es einen Punkt 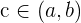 und es gilt
und es gilt 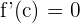 .
.
Grafisch wird der Satz so interpretiert, dass es einen Punkt 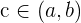 gibt, an dem die Tangente parallel zur x-Achse verläuft (vorausgesetzt, die Annahmen des Satzes sind erfüllt). Sieh dir hierzu die folgende Abbildung an:
gibt, an dem die Tangente parallel zur x-Achse verläuft (vorausgesetzt, die Annahmen des Satzes sind erfüllt). Sieh dir hierzu die folgende Abbildung an:
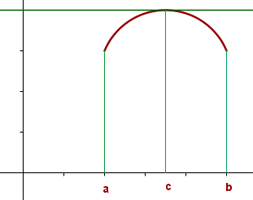
Wenn eine der beiden Annahmen nicht zutrifft, kann man nicht zu dem Schluss kommen, dass es keinen Punkt gibt, an dem 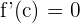 ist. Das heißt, es ist möglich, dass
ist. Das heißt, es ist möglich, dass 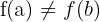 und dass es immer noch einen Punkt
und dass es immer noch einen Punkt 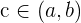 gibt und
gibt und  ist.
ist.
Beispiele und Aufgaben
Überprüfe, ob die Annahmen des Satzes von Rolle für die folgende Funktion erfüllt sind:
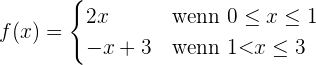
im Intervall 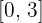 .
.
Wir müssen die drei Annahmen des Satzes von Rolle überprüfen:
\begin{enumerate}
\item Zunächst müssen wir überprüfen, ob die Funktion stetig ist. Wir wissen bereits, dass jedes „Stück“ der Funktion stetig ist, da es sich um Polynome handelt. Daher müssen wir die Stetigkeit nur am Punkt  untersuchen. Wir berechnen zunächst den linken Grenzwert:
untersuchen. Wir berechnen zunächst den linken Grenzwert:

Wir berechnen nur den Grenzwert auf der rechten Seite:
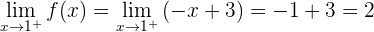
Da die Grenzwerte gleich sind (und die Funktion 2 ist, wenn  ), kommen wir zu dem Schluss, dass die Funktion stetig ist.
), kommen wir zu dem Schluss, dass die Funktion stetig ist.
Nun müssen wir überprüfen, ob die Funktion im gesamten Intervall  differenzierbar ist. Zunächst einmal ist die Funktion in den Intervallen
differenzierbar ist. Zunächst einmal ist die Funktion in den Intervallen  und
und  differenzierbar, da die Funktion in diesen Abschnitten durch Polynome definiert ist.
differenzierbar, da die Funktion in diesen Abschnitten durch Polynome definiert ist.
Daher müssen wir überprüfen, ob die Funktion bei  differenzierbar ist, wozu wir die „seitlichen Ableitungen“ berechnen. Zunächst ermitteln wir die Ableitung der Funktion. Für das Intervall
differenzierbar ist, wozu wir die „seitlichen Ableitungen“ berechnen. Zunächst ermitteln wir die Ableitung der Funktion. Für das Intervall  haben wir:
haben wir:

Für  lautet die Ableitung
lautet die Ableitung
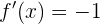
Daraus folgt, dass  . Daher ist die Ableitung bei
. Daher ist die Ableitung bei  nicht definiert und die Funktion ist nicht im gesamten Intervall differenzierbar.
nicht definiert und die Funktion ist nicht im gesamten Intervall differenzierbar.
Daher ist eine der Annahmen falsch. Wir können wir den Satz von Rolle also nicht anwenden, um die Existenz eines Wertes 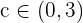 zu gewährleisten, sodass
zu gewährleisten, sodass 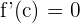 (tatsächlich gibt es keinen solchen Wert).
(tatsächlich gibt es keinen solchen Wert).
Kann der Satz von Rolle bei der Funktion 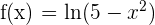 für das Intervall
für das Intervall 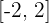 angewendet werden?
angewendet werden?
Auch hier prüfen wir die Annahmen einzeln:
1 Wir wissen, dass die Funktion 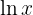 für gesamt
für gesamt 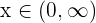 stetig ist. Wenn also das Argument der Funktion größer als 0 (und stetig) ist, dann wissen wir, dass
stetig ist. Wenn also das Argument der Funktion größer als 0 (und stetig) ist, dann wissen wir, dass  ebenfalls stetig ist.
ebenfalls stetig ist.
Da 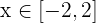 , ist
, ist 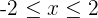 . Daraus folgt:
. Daraus folgt:
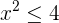
Wenn wir  auf beiden Seiten subtrahieren, erhalten wir
auf beiden Seiten subtrahieren, erhalten wir
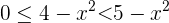
Daraus folgern wir, dass 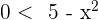 . Außerdem ist
. Außerdem ist 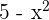 ein Polynom (somit stetig und ableitbar). Also ist
ein Polynom (somit stetig und ableitbar). Also ist

ebenfalls stetig.
2 Die Überprüfung der Differenzierbarkeit ist die gleiche wie die Überprüfung der Stetigkeit. Wir wissen, dass 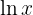 bei
bei 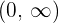 differenzierbar ist. Solange das Argument größer als 0 und differenzierbar ist, ist
differenzierbar ist. Solange das Argument größer als 0 und differenzierbar ist, ist  also auch differenzierbar.
also auch differenzierbar.
Da 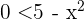 und
und 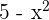 differenzierbar ist, ist
differenzierbar ist, ist  somit auch differenzierbar.
somit auch differenzierbar.
3 Schließlich müssen wir überprüfen, ob  :
:
 ,
,
während
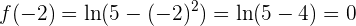 ,
,
wenn gilt, dass  .
.
Daraus schließen wir, dass alle Annahmen des Satzes von Rolle erfüllt sind. Es muss also ein 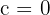 existieren, sodass
existieren, sodass 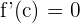 ist. Der Wert von c ist nämlich
ist. Der Wert von c ist nämlich 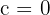 , den man durch Berechnung der Ableitung von
, den man durch Berechnung der Ableitung von  erhält.
erhält.
Wende den Satz von Rolle an, um zu überprüfen, ob 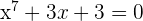 eine einfache Nullstelle hat.
eine einfache Nullstelle hat.
Aufgabe: Wende den Satz von Rolle an.
Das Polynom 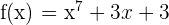 ist ungerade, also muss es mindestens eine Nullstelle haben. Das heißt, es gibt einen Wert
ist ungerade, also muss es mindestens eine Nullstelle haben. Das heißt, es gibt einen Wert  , sodass
, sodass  .
.
Durch den Widerspruchsbeweis nehmen wir an, dass das Polynom zwei oder mehr unterschiedliche Nullstellen hat. Diese Nullstellen seien 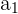 und
und  , wobei
, wobei 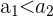 .
.
Wir wissen, dass  ein Polynom ist. Somit ist es stetig und differenzierbar für gesamt
ein Polynom ist. Somit ist es stetig und differenzierbar für gesamt  .
.
Und da 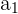 und
und  Nullstellen sind, ist
Nullstellen sind, ist 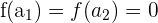 .
.
Deshalb sind die Annahmen des Satzes von Rolle für das Intervall  erfüllt. Nach dem Satz von Rolle muss es also
erfüllt. Nach dem Satz von Rolle muss es also  geben, sodass
geben, sodass 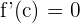 .
.
Jedoch ist die Ableitung von 
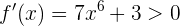 ,
,
die immer größer als 0 ist. Das heißt, es gibt kein  , sodass
, sodass 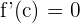 .
.
Hier haben wir also einen Widerspruch (wir sagen, dass  existiert und nicht extistiert). Da dieser Widerspruch aus der Annahme resultiert, dass
existiert und nicht extistiert). Da dieser Widerspruch aus der Annahme resultiert, dass  zwei oder mehr verschiedene Nullstellen hat, können wir daraus schließen, dass
zwei oder mehr verschiedene Nullstellen hat, können wir daraus schließen, dass  genau eine reelle Nullstelle hat.
genau eine reelle Nullstelle hat.
Erfüllt die Funktion 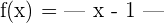 die Annahmen des Satzes von Rolle für das Intervall
die Annahmen des Satzes von Rolle für das Intervall  ?
?
Wir überprüfen die Annahmen einzeln:
1 Wir wissen, dass die Funktion  (Betrag) für gesamt
(Betrag) für gesamt  stetig ist. Somit ist
stetig ist. Somit ist  stetig.
stetig.
2 Um zu überprüfen, ob  differenzierbar ist, beachten wir:
differenzierbar ist, beachten wir:
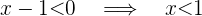
Daher kann die Funktion wie folgt geschrieben werden
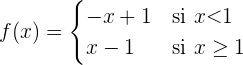
Wir berechnen die links- und rechtsseitigen Ableitungen bei  :
:
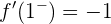
und
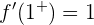 ,
,
woraus folgt, dass 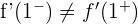 . Somit ist
. Somit ist  im gesamten Intervall
im gesamten Intervall 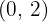 nicht differenzierbar.
nicht differenzierbar.
Folglich sind die Annahmen des Satzes von Rolle nicht erfüllt.
Überprüfe, ob die Funktion 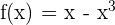 die Annahmen des Satzes von Rolle in den Intervallen
die Annahmen des Satzes von Rolle in den Intervallen  und
und  erfüllt. Falls ja, ermittle die Werte von
erfüllt. Falls ja, ermittle die Werte von  , sodass
, sodass 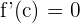 .
.
Da  ein Polynom ist, ist es stetig und differenzierbar für gesamt
ein Polynom ist, ist es stetig und differenzierbar für gesamt  . Daher müssen wir nur überprüfen, ob:
. Daher müssen wir nur überprüfen, ob:
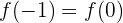
und

Somit gilt für  :
:
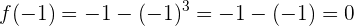
Für  :
:
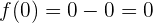
und für  :
:
Somit sind die Annahmen des Satzes von Rolle für die Intervalle  und
und  erfüllt.
erfüllt.
Nun ermitteln wir die Werte von  , sodass
, sodass  . Hierfür berechnen wir zunächst die Ableitung von
. Hierfür berechnen wir zunächst die Ableitung von  :
:
Nun setzen wir gleich 0:
 ,
,
woraus folgt, dass

Somit:
Wir stellen fest, dass  und
und 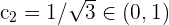 . Somit können wir die Werte von
. Somit können wir die Werte von  bestimmen, sodass
bestimmen, sodass 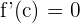 .
.
Überprüfe, ob die Funktion  die Annahmen des Satzes von Rolle im Intervall
die Annahmen des Satzes von Rolle im Intervall  erfüllt.
erfüllt.
Wir müssen die Annahmen eine nach der anderen überprüfen. Stetigkeit und Differenzierbarkeit sind jedoch sehr einfach, da  ein Polynom (und damit differenzierbar und stetig) ist.
ein Polynom (und damit differenzierbar und stetig) ist.
Wir überprüfen, ob 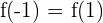 :
:

und

Somit ist 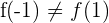 .
.
Daraus können wir schließen, dass die Annahmen des Satzes von Rolle nicht erfüllt sind.
Zeige, dass die Gleichung 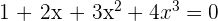 eine einzige Lösung hat.
eine einzige Lösung hat.
Aufgabe: Wende den Satz von Rolle an.
Wie in einer der vorangegangenen Übungen nutzen wir den Widerspruchsbeweis.
Zunächst wissen wir, dass 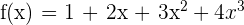 mindestens eine Nullstelle hat, da es sich um ein ungerades Polynom handelt.
mindestens eine Nullstelle hat, da es sich um ein ungerades Polynom handelt.
Durch den Widerspruchsbeweis nehmen wir an, dass mehr als eine reelle Nullstelle existiert. Das heißt, es existieren 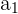 und
und  ,sodass
,sodass 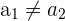 ,
, 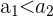 y
y

Da  ein Polynom ist, ist es stetig und differenzierbar. Daher sind alle Annahmen des Satzes von Rolle im Intervall
ein Polynom ist, ist es stetig und differenzierbar. Daher sind alle Annahmen des Satzes von Rolle im Intervall  erfüllt.
erfüllt.
Es muss also  existieren, sodass
existieren, sodass 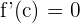 .
.
Die Ableitung von  ist jedoch
ist jedoch
 ,
,
deren Diskriminante wie folgt ist:
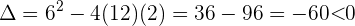 .
.
Das bedeutet, dass  keine Nulltstellen hat und
keine Nulltstellen hat und  nicht existieren, sodass
nicht existieren, sodass 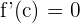 . Wir haben also einen Widerspruch.
. Wir haben also einen Widerspruch.
Daraus folgt, dass  höchstens eine Nullstelle hat.
höchstens eine Nullstelle hat.
Wie viele Nullstellen hat die Gleichung 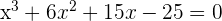 ?
?
Diese Aufgabe ist der vorherigen Aufgabe sehr ähnlich.
Zunächst wissen wir, dass 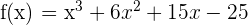 mindestens eine Nullstelle hat, da es sich um ein Polynom ungeraden Grades handelt.
mindestens eine Nullstelle hat, da es sich um ein Polynom ungeraden Grades handelt.
Wir nehmen nun an, dass mehr als eine reelle Nullstelle exitiert. Das heißt, es existieren 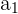 und
und  , sodass
, sodass 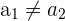 ,
, 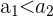 und
und

Auch hier gilt: Da  ein Polynom ist, ist es stetig und differenzierbar. Daher sind alle Annahmen des Satzes von Rolle im Intervall
ein Polynom ist, ist es stetig und differenzierbar. Daher sind alle Annahmen des Satzes von Rolle im Intervall  erfüllt.
erfüllt.
Somit muss  existieren, sodass
existieren, sodass 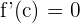 .
.
Jedoch ist die Ableitung von 
 ,
,
deren Diskriminante wie folgt lautet:
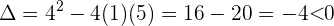
Dies bedeutet, dass  keine Nullstellen hat. Es extistieren also keine
keine Nullstellen hat. Es extistieren also keine  , sodass
, sodass 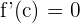 . Wir haben also einen Widerspruch.
. Wir haben also einen Widerspruch.
Wir schließen daraus, dass  höchstens eine Nullstelle hat. Allerdings ist es immer noch möglich, dass es mehrere gleiche Nullstellen gibt (d. h. die Nullstelle hat eine andere Vielfachheit als 1).
höchstens eine Nullstelle hat. Allerdings ist es immer noch möglich, dass es mehrere gleiche Nullstellen gibt (d. h. die Nullstelle hat eine andere Vielfachheit als 1).
Zeige, dass die Gleichung 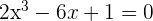 eine einzige reelle Lösung im Intervall
eine einzige reelle Lösung im Intervall  hat.
hat.
Auch hier gehen wir nach dem Prinzip des Widerspruchsbeweises vor. Allerdings wird das Verfahren jetzt etwas anders sein.
Zunächst wissen wir, dass  mindestens eine Nullstelle hat, da es sich um Polynom ungeraden Grades handelt. Allerdings wir können nicht sicher sein, dass sich die Nullstelle im Intervall
mindestens eine Nullstelle hat, da es sich um Polynom ungeraden Grades handelt. Allerdings wir können nicht sicher sein, dass sich die Nullstelle im Intervall  befindet. Dazu werten wir die Funktion an den Grenzwerten des Intervalls aus:
befindet. Dazu werten wir die Funktion an den Grenzwerten des Intervalls aus:
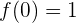
und
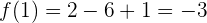
Also ist 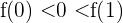 . Und da
. Und da  stetig ist, existiert nach dem Zwischenwertsatz
stetig ist, existiert nach dem Zwischenwertsatz 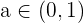 , sodass
, sodass  . Achtung: Wir dürfen den Zwischenwertsatz nicht mit dem Satz von Rolle verwechseln.
. Achtung: Wir dürfen den Zwischenwertsatz nicht mit dem Satz von Rolle verwechseln.
Durch den Widerspruchsbeweis nehmen wir an, dass im Intervall  mehr als eine reelle Nullstelle (verschieden) existiert. Das heißt, es existieren
mehr als eine reelle Nullstelle (verschieden) existiert. Das heißt, es existieren 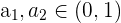 , sodass
, sodass 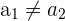 ,
, 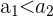 und
und

Da  ein Polynom ist, ist es stetig und differenzierbar. Daher sind alle Annahmen des Satzes von Rolle im Intervall
ein Polynom ist, ist es stetig und differenzierbar. Daher sind alle Annahmen des Satzes von Rolle im Intervall  erfüllt.
erfüllt.
Es muss also 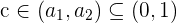 existieren, sodass
existieren, sodass 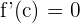 . Es ist zu beachten, dass
. Es ist zu beachten, dass 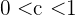 erfüllt sein muss. Es muss gelten:
erfüllt sein muss. Es muss gelten: 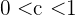 .
.
Die Ableitung von  ist schließlich
ist schließlich
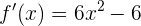
wir setzen gleich 0 und erhalten

Das heißt, 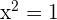 . Die Nullstellen sind also
. Die Nullstellen sind also  und
und  . Jedoch befindet sich keine dieser Nullstellen im Intervall
. Jedoch befindet sich keine dieser Nullstellen im Intervall  , was dem Satz von Rolle widerspricht.
, was dem Satz von Rolle widerspricht.
Wir schließen daraus, dass  eine einzige Nullstelle im Intervall
eine einzige Nullstelle im Intervall  hat.
hat.












