Steigung der Tangente
Die Steigung der Tangente, die einen Graphen an einem Punkt berührt, ist gleich der Ableitung der Funktion an diesem Punkt.
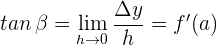
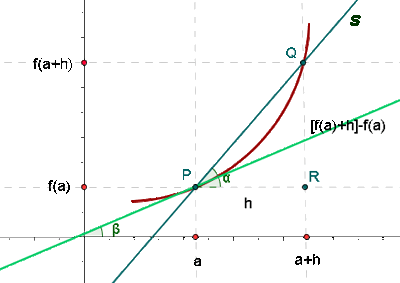
Beispiel: Berechne die Steigung der Tangente am Funktionsgraphen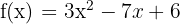 
für 
1 Wir berechnen die Ableitung
2 Die gesuchte Steigung ist
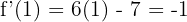
Gleichung der Tangente
Die Tangente an einem Punkt eines Funktionsgraphen verläuft durch den Punkt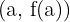 
und ihre Steigung ist gleich 
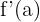. Sie ist gegeben durch
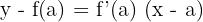
Beispiel: Bestimme die Tangente an dem Graphen 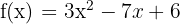bei
1 Wir berechnen den Punkt auf dem Graphen, durch den die Tangente verläuft
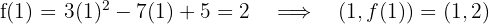
2 Wir berechnen die Steigung der Tangente bei 
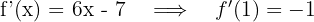
3 Die Gleichung der Tangente ist
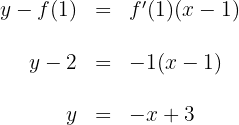
Aufgaben mit Lösungen
Berechne die Punkte, an denen die Tangente an dem Graphen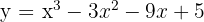 
parallel zur 
-Achse ist.
1 Berechne die Ableitung des Funktionsgraphen
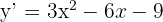
2 Die -Achse hat die Steigung 0 und die Steigung der Tangente ist gleich der Ableitung. Die parallelen Geraden haben dieselbe Steigung
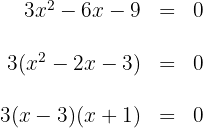
die Werte für sind somit 
und 
3 Wir berechnen die Werte 
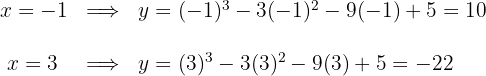
Die gesuchten Punkte si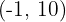nd 
und 
Es wird eine Tangente an dem Graphen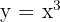 
gezeichnet, deren Steigung 
ist und die durch den Punkt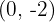 
verläuft. Ermittle den Berührungspunkt.
1 Wir berechnen die Ableitung des Funktionsgraphen
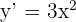
2 Da die Steigung ist, setzen wir sie gleich der Ableitung und bestimmen die Werte der Berührungspunkte mit der Steigung 3
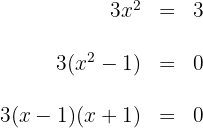
somit gelten für die Werte und
3 Wir berechnen die Werte
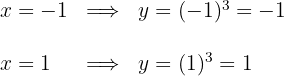
Die gesuchten Punkte si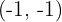nd 
und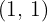 
4 Die Gleichung der Tangente mit dem Berührungspunk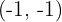t ist
,
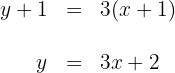die nicht durch den Punkt 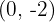verläuft.
Die Gleichung der Tangente mit dem Berührungspunk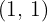t ist
,
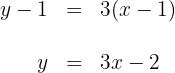die durch den Punkt 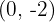verläuft. Somit ist der gesuchte Punkt der Tangente .
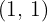Bestimme die Punkte des Funktionsgraphen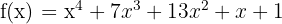 
, für die die Tangente einen Winkel von 
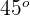mit der -Achse bildet.
1 Wir berechnen die Ableitung des Funktionsgraphen
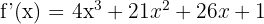
2 Die Steigung ist gleich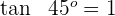 
. Wir setzen diese Steigung gleich der Ableitung und ermitteln die Werte der Berührungspunkte mit der Steigung 3
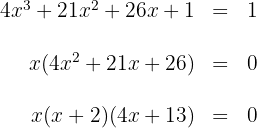
für gilt 
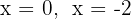und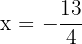 
3 Wir berechnen die Werte der 2. Koordinate der Berührungspunkte
Die gesuchten Punkte si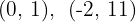nd 
und 
Gegeben ist die Funktion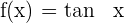 
. Bestimme den Winkel, den die Tangente an den Graphen der Funktion 
im Ursprung mit der x-Achse bildet.
1 Wir berechnen die Ableitung des Funktionsgraphen
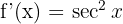
2 Die Steigung im Ursprung ist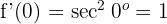 
. Somit ist der durch die Tangente und die x-Achse gebildete Winkel
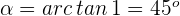
Bestimme die Koeffizienten der Gleichung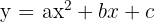 
. Ihr Graph verläuft durch die Punkte 
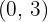und 
. Die Tangente hat an diesem letzten Punkt eine Steigung von .
1 Wir berechnen die Ableitung des Funktionsgraphen
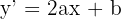
2 Wenn man die beiden Punkte, durch die der Graph verläuft, in die gegebene Gleichung und die Steigung der Tangente einsetzt, erhält man das folgende System mit 3 Gleichungen
3 Das Gleichungssystem
hat die Lösung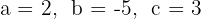 
Bestimme die Koeffizienten der Gleichung 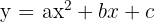. Ihr Graph verläuft durch die Punkte 
und 
, wobei die Tangente an den Punkt der x-Achse 
parallel zur Winkelhalbierenden des 1. Quadranten verläuft. Ermittle den numerischen Wert der Koeffizienten der Gleichung.
1 Wir berechnen die Ableitung des Funktionsgraphen
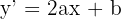
2 Setzt man die beiden Punkte, durch die der Graph verläuft, in die gegebene Gleichung und die Steigung der Tangente, die ist, erhält man das folgende System mit 3 Gleichungen
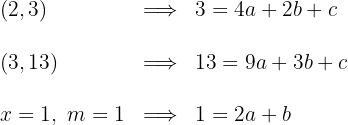
3 Das Gleichungssystem
hat die Lösung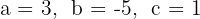 
Bestimme die Koeffizienten der Gleichung 
. Ihr Graph verläuft durch die Punkte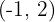 
und , wobei die Tangente an den Punkten und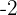 
auf der x-Achse parallel zur x-Achse verläuft. Ermittle den numerischen Wert der Koeffizienten der Gleichung.
1 Wir berechnen die Ableitung des Funktionsgraphen
2 Setzt man die beiden Punkte, durch die der Graph verläuft, in die gegebene Gleichung und die Steigung der Tangente, die 
ist, ein, so erhält man das folgende System mit 4 Gleichungen
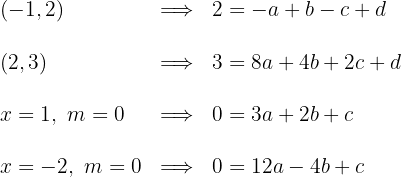
3 Das Gleichungssystem
hat die Lösung 
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
