Willkommen in unserem Bereich mit Übungen zur Definition der Ableitung. Die Ableitung ist ein grundlegendes Konzept in der Infinitesimalrechnung und der mathematischen Analyse, das die momentane Änderungsrate einer Funktion an einem bestimmten Punkt beschreibt. Mit anderen Worten, sie stellt dar, wie sich eine Funktion in Reaktion auf infinitesimale Änderungen ihrer unabhängigen Variablen verändert.
Die Ableitung einer Funktion  an einem Punkt
an einem Punkt  wird üblicherweise mit
wird üblicherweise mit 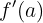 bezeichnet. Mathematisch gesehen ist die Ableitung durch den Grenzwert definiert:
bezeichnet. Mathematisch gesehen ist die Ableitung durch den Grenzwert definiert:
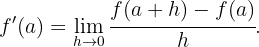
Wenn dieser Grenzwert existiert, ist die Funktion im Punkt  ableitbar oder differenzierbar. Geometrisch gesehen stellt die Ableitung an einem Punkt die Steigung der Tangente an den Graphen der Funktion in diesem Punkt dar. Berechne nun anhand der Definition der Ableitung die Ableitung der Funktionen an den angegebenen Punkten.
ableitbar oder differenzierbar. Geometrisch gesehen stellt die Ableitung an einem Punkt die Steigung der Tangente an den Graphen der Funktion in diesem Punkt dar. Berechne nun anhand der Definition der Ableitung die Ableitung der Funktionen an den angegebenen Punkten.
 für
für 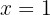
Wir setzen den Wert von  in die Funktion und in die Definition der Ableitung ein:
in die Funktion und in die Definition der Ableitung ein:
1
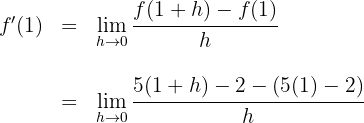
2
Wir lösen und berechnen den Grenzwert

 für
für 
 für
für 
1
Wir setzen den Wert von  in die Funktion und in die Definition der Ableitung ein:
in die Funktion und in die Definition der Ableitung ein: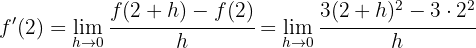
2
Wir lösen und berechnen den Grenzwert

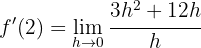
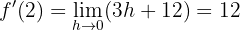
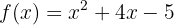 für
für 
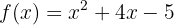
1
Wir setzen den Wert von  in die Funktion und in die Definition der Ableitung ein:
in die Funktion und in die Definition der Ableitung ein:
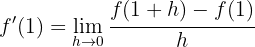

2
Wir lösen und berechnen den Grenzwert
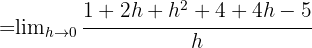

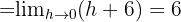
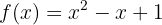 für
für 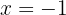 ,
,  und
und 
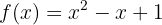 für
für  ,
,  und
und 
1
Wir berechnen die Ableitung
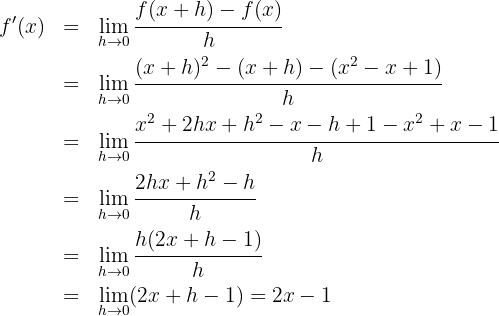
2
Wir setzen  ,
,  und
und  in die Ableitung ein.
in die Ableitung ein.
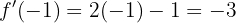
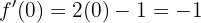
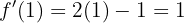
 für
für 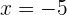
 für
für 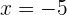
1
Wir berechnen die Ableitung der Funktion, indem wir die Definition anwenden: 



2
Wir setzen 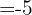 in die Ableitung ein
in die Ableitung ein
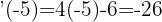
 für
für 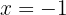
1
Wir setzen den Wert von  in die Funktion und in die Definition der Ableitung ein:
in die Funktion und in die Definition der Ableitung ein:
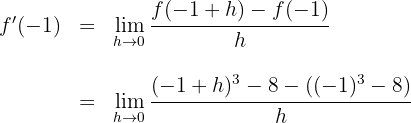
2
Wir lösen und berechnen den Grenzwert

 für
für 
 für
für 
1
Wir berechnen die Ableitung der Funktion: 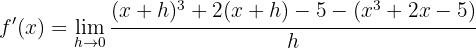
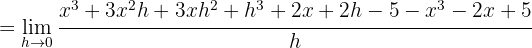
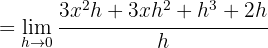

2
Wir setzen  in die Ableitung ein
in die Ableitung ein

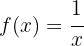 für
für 
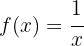 für
für 
1
Wir berechnen die Ableitung der Funktion
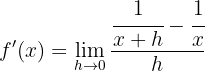



2
Wir setzen  in die Ableitung ein
in die Ableitung ein
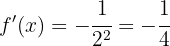
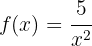 für
für 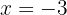
1
Wir setzen den Wert von  in die Funktion und in die Definition der Ableitung ein:
in die Funktion und in die Definition der Ableitung ein:
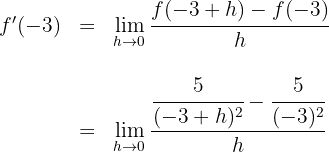
2
Wir lösen und berechnen den Grenzwert
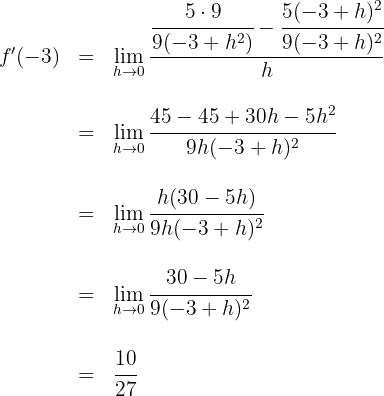
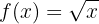 für
für 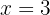
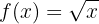 für
für 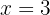
Wir setzen den Wert von 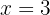 ein und lösen den Grenzwert
ein und lösen den Grenzwert 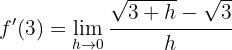
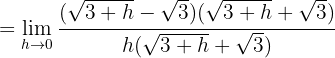


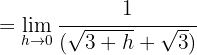
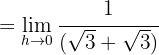
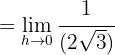
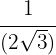
 für
für 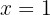
1
Wir setzen den Wert von  in die Funktion und in die Definition der Ableitung ein:
in die Funktion und in die Definition der Ableitung ein:
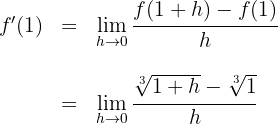
2
Wir lösen und berechnen den Grenzwert
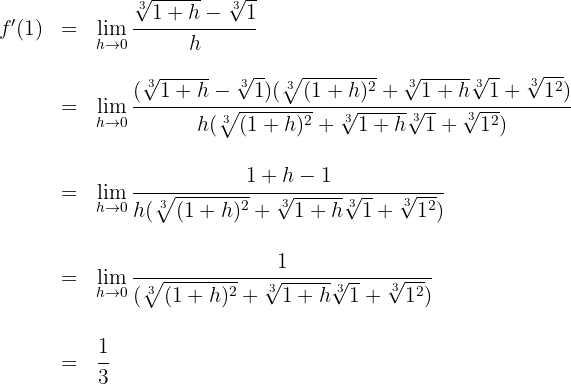
 für
für 
 für
für 
1
Wir berechnen die Ableitung der Funktion, indem wir die Definition anwenden
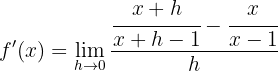
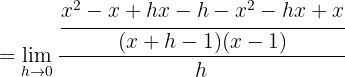
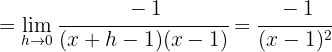
2
Wir setzen  in die Ableitung ein
in die Ableitung ein
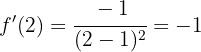
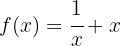 für
für 
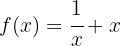 für
für 
1
Wir berechnen die Ableitung der Funktion, indem wir die Definition anwenden
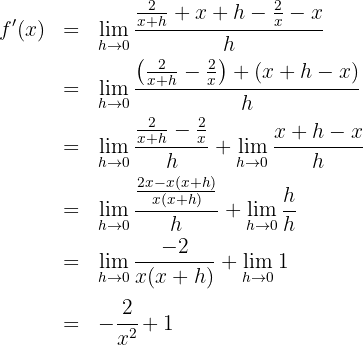
2
Wir setzen  in die Ableitung ein
in die Ableitung ein
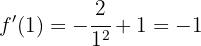
 für
für 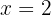
1
Wir setzen den Wert von  in die Funktion und in die Definition der Ableitung ein:
in die Funktion und in die Definition der Ableitung ein:
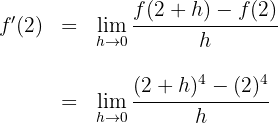
2
Wir lösen und berechnen den Grenzwert
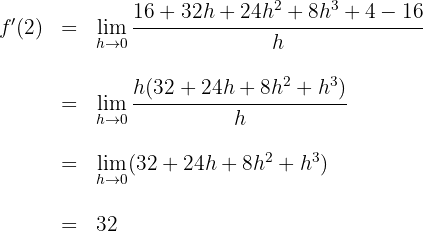
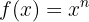 , wenn
, wenn 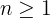 , für
, für 
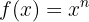 , wenn
, wenn 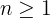 , für
, für 
1
Wir berechnen die Ableitung der Funktion
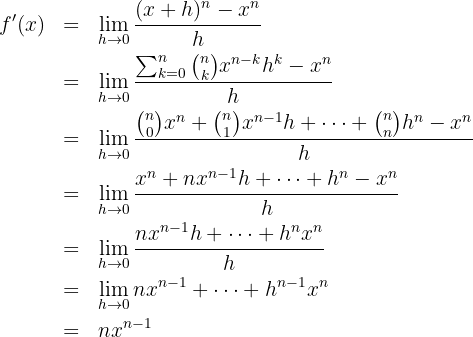
2
Wir setzen  in die Ableitung ein
in die Ableitung ein
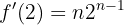
Mit KI zusammenfassen:


