Wenn  eine ableitbare Funktion ist, ist das Differential einer Funktion entsprechend dem Zuwachs
eine ableitbare Funktion ist, ist das Differential einer Funktion entsprechend dem Zuwachs  der unabhängigen Variable das Produkt
der unabhängigen Variable das Produkt 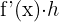 .
.
Das Differential einer Funktion wird mit 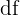 oder
oder  dargestellt.
dargestellt.



Geometrische Interpretation des Differentials
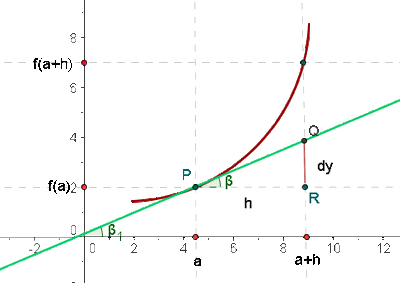
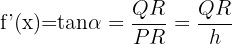
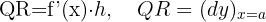
Das Differential in einem Punkt stellt den Zuwachs der Ordinate des Tangens dar, der einem Zuwachs der unabhängigen Variablen entspricht.
Beispiele für Differentiale
1 Hallar la diferencial de 
Wir berechnen die Ableitung der Funktion
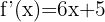
Somit entspricht das Differential der Ableitung der Funktion mal dem Zuwachs
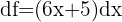
2 Berechne das Differential von 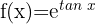
Wir berechnen die Ableitung der Funktion
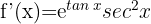
Somit entspricht das Differential der Ableitung der Funktion mal dem Zuwachs
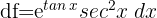
3 Berechne das Differential von 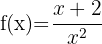
Wir berechnen die Ableitung der Funktion
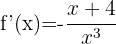
Somit entspricht das Differential der Ableitung der Funktion mal dem Zuwachs
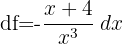
4 Berechne das Differential von 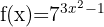
Wir berechnen die Ableitung der Funktion
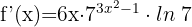
Somit entspricht das Differential der Ableitung der Funktion mal dem Zuwachs

5 Berechne das Differential von 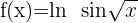
Wir berechnen die Ableitung der Funktion
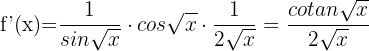
Somit entspricht das Differential der Ableitung der Funktion mal dem Zuwachs
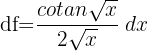
6 Berechne das Differential von 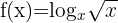
Wir wenden die Definition des Logarithmus an:

Wir wenden  auf beiden Seiten der Gleichheit an:
auf beiden Seiten der Gleichheit an:
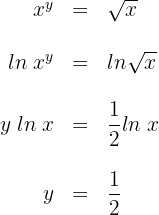
Somit ist 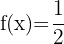 und ihre Ableitung ist
und ihre Ableitung ist 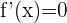
Das Differential ist 
7Ein Quadrat hat eine Seitenlänge von 2 m. Bestimme, um wie viel sich die Fläche des Quadrats vergrößert, wenn seine Seitenlänge um 1 Millimeter zunimmt. Berechne den Fehler, der entsteht, wenn man Differentiale anstelle von Zuwächsen verwendet
Die Fläche des Quadrats ist 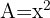
Wir berechnen den Zuwachs
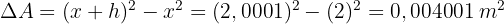
Wir berechnen das Differential
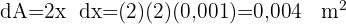
Wir berechnen den Fehler
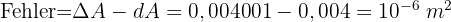
8Berechne die Änderung des Volumens eines Würfels mit einer Kantenlänge von 20 cm, wenn diese Länge um 0,2 cm zunimmt.
Das Volumen des Würfels ist 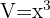
Wir berechnen das Differential
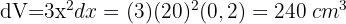
9Berechne den absoluten und relativen Fehler bei der Berechnung des Volumens einer Kugel mit einem Durchmesser von 12,51 mm, gemessen mit einem Instrument, das Tausendstel Zentimeter anzeigt.
Das Volumen der Kugel ist 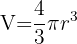
Wir berechnen den Fehler
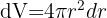
Der Radius der Kugel ist 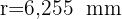 und das Differential ist
und das Differential ist 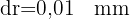
Wir berechnen den absoluten Fehler
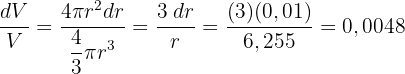
10Wenn 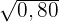 anstatt
anstatt 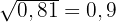 genommen wird, was sind dann die Annäherungen des absoluten und relativen Fehlers?
genommen wird, was sind dann die Annäherungen des absoluten und relativen Fehlers?
Die anzuwendende Funktion lautet 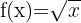
Wir berechnen das Differential von  und
und 
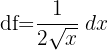
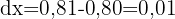
Wir berechnen den relativen Fehler
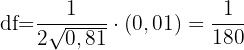
Wir berechnen den absoluten Fehler
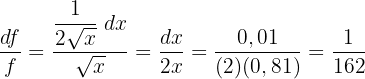
11 Berechne den Zuwachs der Fläche des Quadrats mit einer Seitenlänge von 2 m, wenn wir seine Seitenlänge um 1 mm vergrößern.
Die Fläche des Quadrats ist 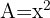
Wir berechnen das Differential und wenden an, dass 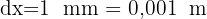
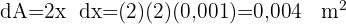
Mit KI zusammenfassen:












