Kapitel

Wendepunkte
Die Wendepunkte einer Funktion sind die Punkte, an denen der Graph der Funktion konkav wird, d. h. von konkav zu konvex oder umgekehrt. Vereinfacht ausgedrückt kann man sagen, dass dies der Moment ist, in dem die Funktion ihre Krümmung ändert.
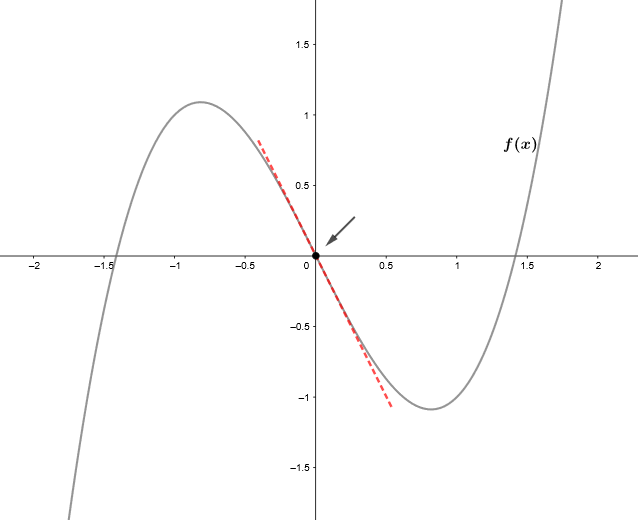
Die Wendepunkte mithilfe der 3. Ableitung ermitteln
Um die Wendepunkte einer ableitbaren Funktion  mithilfe der 3. Ableitung zu bestimmen, führen wir folgende Schritte durch.
mithilfe der 3. Ableitung zu bestimmen, führen wir folgende Schritte durch.
1 Wir ermitteln die 1. Ableitung von  :
:  .
.
2 Wir ermitteln die 2. Ableitung von  und setzen gleich 0:
und setzen gleich 0:  .
.
3 Wir bestimmen die unabhängige Variable " " und ermitteln die Werte, für die die Bedingung erfüllt wird. Das heißt, wir suchen die
" und ermitteln die Werte, für die die Bedingung erfüllt wird. Das heißt, wir suchen die 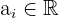 sowie
sowie 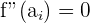 mit
mit  .
.
4 Wir ermitteln die 3. Ableitung von  :
: 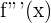 .
.
5 Wir setzen 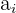 in die 3. Ableitung ein. Wenn
in die 3. Ableitung ein. Wenn  , gibt es einen Wendepunkt bei
, gibt es einen Wendepunkt bei 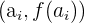 .
.
Beispiel: Berechnung der Wendepunkte anhand der 3. Ableitung.
Berechne die Wendepunkte von:
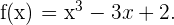
Lösung: Wir befolgen die oben beschriebenen Schritte, um die Wendepunkte zu ermitteln.
1 Wir ermitteln die 1. Ableitung von 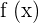 :
: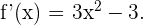
2 Wir ermitteln die 2. Ableitung von  und setzen gleich 0:
und setzen gleich 0: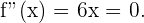
3 Wir berechnen die Nullstellen von 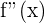 und erhalten
und erhalten . Das heißt,
. Das heißt, 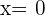 ist eine Nullstelle von
ist eine Nullstelle von 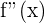 .
.
4 Wir berechnen die 3. Ableitung von  :
: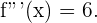
5 Wir setzen  in die 3. Ableitung ein:
in die 3. Ableitung ein: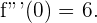
Da  , ist
, ist 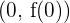 ein Wendepunkt, wobei
ein Wendepunkt, wobei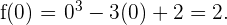 Somit ist der Punkt
Somit ist der Punkt  ein Wendepunkt.
ein Wendepunkt.
Berechnung von Wendepunkten bei Kenntnis der Konkavitäts- und Konvexitätsintervalle
Wir berechnen die Wendepunkte der folgenden Funktionen, indem wir die Intervalle der Konkavität und Konvexität hinzu ziehen.
1 
Lösung:
Wir beginnen mit der Analyse des Definitionsbereichs der Funktion. Wir stellen fest, dass  nicht definiert ist, wenn der Nenner 0 wird. Somit verwerfen wir die Werte, für die der Nenner 0 wird:
nicht definiert ist, wenn der Nenner 0 wird. Somit verwerfen wir die Werte, für die der Nenner 0 wird: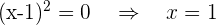
und somit 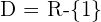 .
.
Wir fahren mit der Berechnung der 1. und 2. Ableitung von  fort, um mögliche Wendepunkte zu finden:
fort, um mögliche Wendepunkte zu finden:

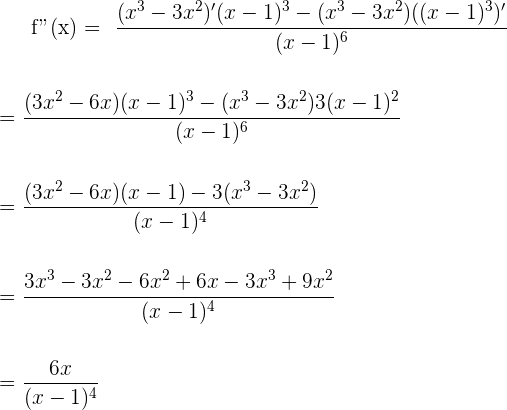
Wir setzen die 2. Ableitung gleich 0: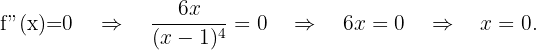
Somit befindet sich ein möglicher Wendepunkt bei 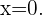
Nun gibt es eine Eigenschaft der 2. Ableitung, die uns sagt: Wenn die 2. Ableitung von  in einem Intervall positiv ist, ist
in einem Intervall positiv ist, ist  in diesem Intervall konvex. Und: Wenn die 2. Ableitung von
in diesem Intervall konvex. Und: Wenn die 2. Ableitung von  in einem Intervall negativ ist, ist
in einem Intervall negativ ist, ist  in diesem Intervall konkav. Unter Berücksichtigung dieser Tatsache überprüfen wir die Vorzeichen, indem wir den Definitionsbereich segmentieren:
in diesem Intervall konkav. Unter Berücksichtigung dieser Tatsache überprüfen wir die Vorzeichen, indem wir den Definitionsbereich segmentieren:
- Wenn
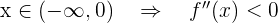
- Wenn
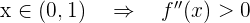
- Wenn
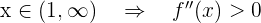 .
.
Die Funktion ist konkav im Intervall  und konvex im Intervall
und konvex im Intervall  . Da die Funktion am Punkt
. Da die Funktion am Punkt  von konkav zu konvex wechselt, ist der Punkt
von konkav zu konvex wechselt, ist der Punkt 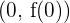 somit ein Wendepunkt. Das heißt, im Punkt
somit ein Wendepunkt. Das heißt, im Punkt  .
.
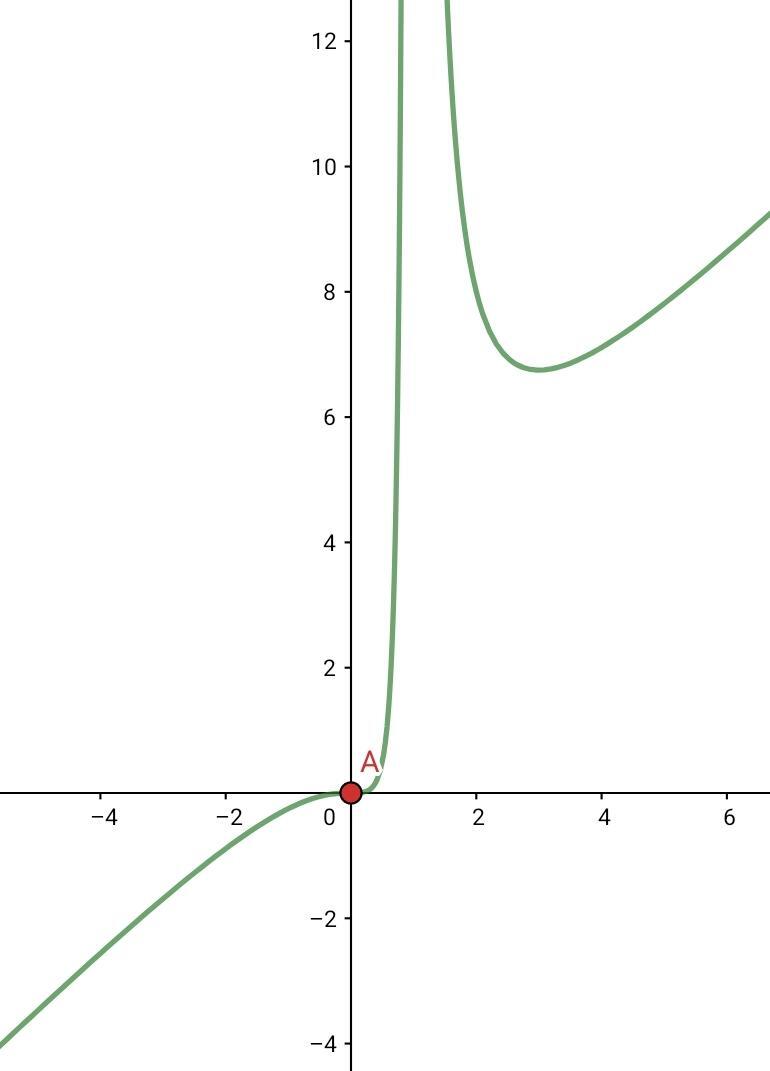
2 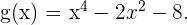
Lösung:
Man beachte, dass in diesem Fall kein Problem besteht, da es sich um eine Polynomfunktion handelt, weshalb  . Wir berechnen die 1. und 2. Ableitung.
. Wir berechnen die 1. und 2. Ableitung.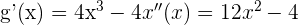
Wir setzen die 2. Ableitung gleich 0 und berechnen die Nullstellen
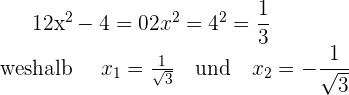
Nun gilt:
- Wenn
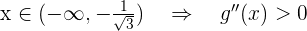 ,
, - Wenn
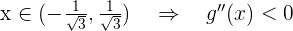 , y
, y - Wenn
 ,
,
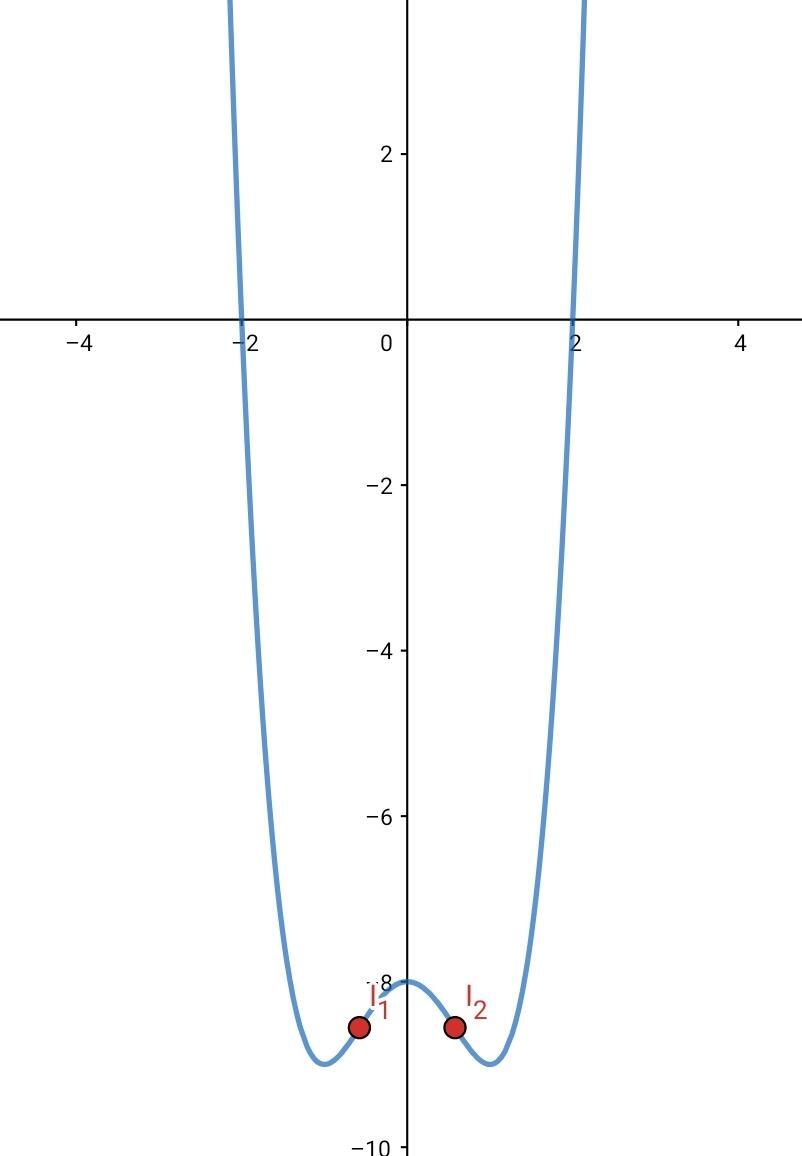
Ähnlich wie in der vorherigen Übung zeigt dies, dass  bei
bei 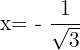 von konvex zu konkav wird
von konvex zu konkav wird 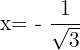 und konkav bei konvex bei
und konkav bei konvex bei 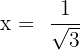 . Daraus können wir auf folgende Wendepunkte schließen:
. Daraus können wir auf folgende Wendepunkte schließen:
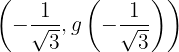 . Das heißt, im Punkt
. Das heißt, im Punkt 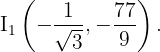
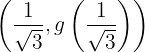 . Das heißt, im Punkt
. Das heißt, im Punkt 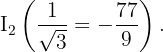
Aufgaben zu Wendepunkten
1 Ermittle die Gleichung der Tangente des Graphen 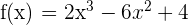 an seinem Wendepunkt.
an seinem Wendepunkt.
Lösung:
Zunächst ermitteln wir den Wendepunkt von  . Hierfür berechnen wir die 1. und 2. Ableitung von
. Hierfür berechnen wir die 1. und 2. Ableitung von  :
: 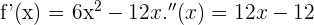
Wir setzen die 2. Ableitung gleich 0 und bestimmen die Werte, für die 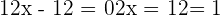 0 wird.
0 wird.
Nun berechnen wir die 3. Ableitung von  und überprüfen, ob
und überprüfen, ob 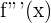 bei
bei  0 wird.
0 wird.
Da 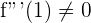 , ist
, ist 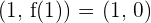 ein Wendepunkt.
ein Wendepunkt.
Nun möchten wir die Gleichung der Tangente im Punkt 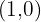 ermitteln. Hierfür nutzen wir die Punkt-Steigungs-Form der Geraden
ermitteln. Hierfür nutzen wir die Punkt-Steigungs-Form der Geraden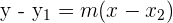 ,
,
wobei  der Punkt der Geraden und
der Punkt der Geraden und  die Steigung der Geraden ist.
die Steigung der Geraden ist.
Wir berechnen die Steigung der Tangente im Punkt 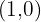 anhand der 1. Ableitung
anhand der 1. Ableitung
Somit lautet die Tangentengleichung
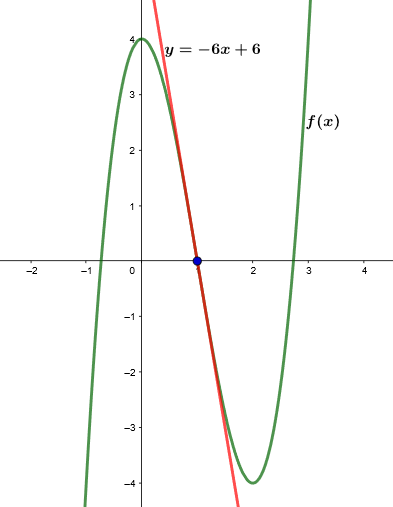
2 Der Graph 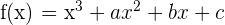 schneidet die x-Achse bei
schneidet die x-Achse bei  und hat einen Wendepunkt bei
und hat einen Wendepunkt bei 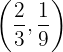 . Ermittle
. Ermittle  und
und  .
.
Lösung:
Wir haben 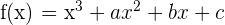 mit den Ableitungen
mit den Ableitungen 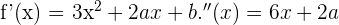
Nun wissen wir, dass  die x-Achse bei
die x-Achse bei 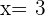 schneidet und somit
schneidet und somit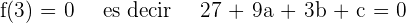
Außerdem wissen wir, dass der Wendepunkt bei 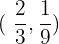 liegt, weshalb die 2. Ableitung bei
liegt, weshalb die 2. Ableitung bei 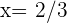 und
und 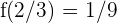 0 werden muss. Das heißt:
0 werden muss. Das heißt: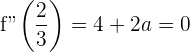
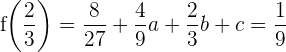
Aus (2) folgt, dass  . Wir setzen den Wert für
. Wir setzen den Wert für  in (1) y (3) ein und:
in (1) y (3) ein und:
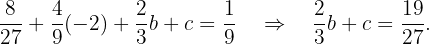
Somit erhalten wir ein lineares Gleichungssystem  :
: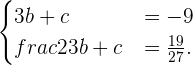
Wir lösen das Gleichungssystem mit einer Methode unserer Wahl und erhalten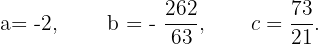
3 Ermittle die Gleichungen der Tangente und der Normalgeraden in ihrem Wendepunkt des Graphen: 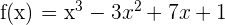 .
.
Lösung:
Wir gehen ähnlich wie bei Problem 1 vor. Aber diesmal unter Berücksichtigung der Tatsache, dass die Gleichung der Normalgeraden im Punkt  wie folgt ist:
wie folgt ist: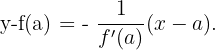
Wir beginnen, indem wir den Wendepunkt von  bestimmen und hierfür berechnen wir die 1. und 2. Ableitung
bestimmen und hierfür berechnen wir die 1. und 2. Ableitung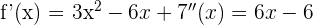
Wir setzen die 2. Ableitung gleich 0 und bestimmen die Nullstellen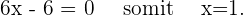
Wir ermitteln die 3. Ableitung und überprüfen, ob sie in 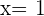 0 wird
0 wird
Somit ist 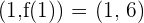 ein Wendepunkt.
ein Wendepunkt.
Da 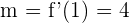 , ist
, ist
Tangente: 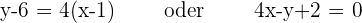
Normalgerade: 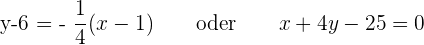
4 Gegeben ist 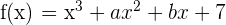 . Ermittle
. Ermittle  und
und  so, dass der Graph der Funktion
so, dass der Graph der Funktion  für
für 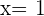 einen Wendepunkt hat und seine Tangente an diesem Punkt einen Winkel von
einen Wendepunkt hat und seine Tangente an diesem Punkt einen Winkel von 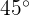 mit der Achse
mit der Achse  bildet.
bildet.
Lösung:
Wir beginnen mit der Berechnung der 1. und 2. Ableitung
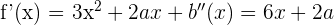
Da wir einen Winkel von 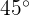 mit der Achse
mit der Achse  am Wendepunkt haben möchten, muss
am Wendepunkt haben möchten, muss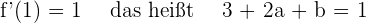
und außerdem soll ein Wendepunkt bei 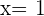 liegen. Somit
liegen. Somit
Wir lösen das Gleichunssystem, das (4) und (5) bilden und erhalten
Mit KI zusammenfassen:












